地震波吸收衰减模拟及反滤波处理

Seismic Wave Absorption and Attenuation Simulation and Anti-Q Filter Processing

摘要: 地震波在地层中的衰减属性用品质因子Q来表示，Q值越大，衰减越弱，Q值越小，衰减越强。反Q滤波是一种补偿大地滤波效应的技术，在已知Q值的情况下，进行反Q滤波可以达到改善地震资料品质的目的。本文数值模拟了地震波的衰减效应，并进行了反Q滤波处理，消除了地层对地震波的衰减效应，取得了较好的效果。

Abstract: The attenuation attribute of seismic wave in the stratum is expressed by the quality factor Q. The larger the Q value is, the weaker the attenuation is. The smaller the Q value is, the stronger the attenuation is. Anti-Q filtering is a technique to compensate the effect of geodetic filtering. Under the condition of known Q value, the quality of seismic data can be improved by using anti-Q filtering. In this paper, the attenuation effect of seismic wave is simulated numerically, and the anti-Q filtering is carried out to eliminate the attenuation effect of strata on seismic wave, and good results are obtained.

1. 概述

地震波能量的衰减可以分为两部分：固有衰减和非固有衰减。其中，固有衰减与介质的粘弹性有关，这一性质使地震波在传播过程中的振动能量因转化为热能而耗损掉，由此造成能量的衰减；非固有衰减由介质的几何构造和震源的几何扩散引起，是一种对地震波能量的重新分配，而不是地震波能量的损失，其衰减机理主要与波阻抗界面对地震波的反射和透射，导致能量的重新分配以及三维非均匀散射体引起的能量向各个方向的分散特性有关 [1] [2]，本文主要分析讨论的衰减是固有衰减。

地震波在地下介质中传播时，能量会随地震波传播距离的增加而发生衰减。这种由于介质粘弹性而产生能量衰减的性质可以用具体的参数来表示。品质因子Q是描述地震波衰减性质的一个重要参数，它详细描述了地层的非完全弹性特质。一般来说，当地震波在粘弹性介质中传播时，通常使用介质的品质因子Q来表征地震波的能量衰减 [3] [4] [5] [6]。

在已知Q值的情况下，对衰减后的地震记录进行反Q滤波处理，可以达到改善地震资料质量的目的。通过反Q滤波，可以补偿地震波在传播过程中的能量衰减、频率缺失和相位畸变，处理后的剖面频带会变宽、主频会增高、能量会加强，分辨率显著提高。这里我们基于Futterman模型对地震波衰减和反Q滤波进行了数值模拟和处理，得到一些认识和结论 [7] [8] [9] [10] [11]。

2. 方法原理

2.1. 品质因子Q

品质因子Q是描述地震波衰减性质的一个重要参数，它详细描述了地层的非完全弹性特质。一般来说，当地震波在粘弹性介质中传播时，通常使用介质的品质因子Q来表征地震波的能量衰减。Q的含义为：地震波传播一个波长的距离后，储能与耗散能的比。表达式如下：

$\frac{1}{Q}=\frac{\Delta E}{2\pi E}$ (1)

式中，ΔE是地震波振动一个周期产生的能量损失，E是地震波在最大应变条件下的能量，显然，Q值越大，损失能量越少；反之，损失能量越多。

2.2. 影响地震波衰减的因素

地震波在介质中传播时发生衰减的影响因素主要有频率、岩性、压力、温度、饱和度和应变振幅等。目前还没有完全统一的结论确定Q值是否与频率有关，但研究表明在干燥的岩石中，Q值与频率无关，但在饱和的岩石中，Q值是与频率有关的。在超声波的频段范围内，Q值与频率的变化有一定关系，但在勘探地震的频率范围内，Q值可以看作是与频率无关的物理量。对频率相同的地震波而言，火成岩、变质岩和结晶岩的Q值最大，页岩次之，砂岩再次之，未固结成岩的地层Q值最小。这是不同岩石具有不同密度、孔隙度和成岩压力作用的综合结果。和速度类似，压力对地层衰减作用的影响很大。地层衰减随压力增大而减小，最终会在达到某个高压值后趋于常数。这是因为，当地层有效压力增大时，地层会被压实，从而导致岩石中裂隙和孔隙的闭合，岩石的骨架硬度得到加强，最终使地层对地震波的吸收降低，也就是地层衰减减小，Q值增大。当温度高于150℃的时候，Q值会随温度的增加而增加，尤其是在接近流体沸点的温度附近，Q值会随温度发生剧烈的变化；而在温度低于150℃时，Q值与温度变化基本无关。当岩石完全饱和或部分饱和时，其Q值比干燥的岩石要小。对于纵波来说，干燥的岩石Q值最大，加入少量水后Q值会减小，继续加水后Q值会一直减小，并在加水至岩石饱和度为80%~90%时到达峰值，这是由于岩体孔隙中气泡的形成产生了能量的损耗。对于小应变情况，衰减与应变振幅无关，而当应变振幅大于10⁻⁶时，衰减迅速增加。在震源附近，地震波的振幅很强，颗粒间的摩擦作用很强，Q值很小。

2.3. Futterman模型

Futterman对统一的黏弹性介质模型进行了研究，率先总结出了品质因子与频率的关系式，后人将其所做工作称为Futterman模型 [12]。由于Futterman模型相对简单，所需参数容易估算，是常用的衰减模型。

假设振幅为 $A_0\left(f\right)$ 的地震波，传播时间t以后振幅衰减为： $A(\; f\; )$

$A\left(f\right)=A_0\left(f\right)\exp \left(-\frac{\pi f}{Q}t\right)$ (2)

其中，Q为品质因子，f为频率。从上式可以看出，当Q值为常量时，介质对地震波的吸收效应是时变的低通滤波器。介质吸收因子的振幅谱 $AMP\left(f\right)$ 为：

$AMP\left(f\right)=\exp \left(-\frac{\pi f}{Q}t\right)$ (3)

取振幅谱的对数作希尔伯特变换，得到介质吸收因子的相位谱 $\phi \left(f\right)$ ：

$\phi \left(f\right)=H\left\{\ln \left[AMP\left(f\right)\right]\right\}=H\left\{\ln \left[\exp \left(-\frac{\pi f}{Q}t\right)\right]\right\}=-\frac{\pi t}{Q}H\left(f\right)$ (4)

式中 $H\left\{\right\}$ 为希尔伯特变换。则吸收因子的频谱 $S\left(f\right)$ ：

$\begin{array}{l}S\left(f\right)=AMP\left(f\right)\exp \left[i\phi \left(f\right)\right]=\exp \left(-\frac{\pi f}{Q}t\right)\exp \left[-\frac{i\pi f}{Q}H\left(f\right)\right]\\ \Rightarrow S\left(f\right)=\exp \left\{-\frac{\pi t}{Q}\left[f+iH\left(f\right)\right]\right\}\end{array}$ (5)

式(4)就是Futterman模型。其中，f为频率；t旅行时；Q为品质因子，一般认为Futterman模型中的Q值是一个常数，不随频率的变化而发生改变； $H\left(f\right)$ 是f的希尔伯特变换。

Futterman模型说明地震波呈负指数衰减并且是最小相位的。衰减量与频率f、时间t以及品质因子Q有关。频率和时间与衰减量成正比，品质因子与衰减量呈反比，这就是普遍存在于大地滤波过程中的地震波场衰减规律。Futterman模型可以较准确地描述地震波在介质中的衰减性质且表达式较为简洁，本文所有的运算均基于Futterman模型进行实现。

2.4. 吸收衰减模拟

令震源为雷克子波，其频谱 $R\left(f\right)$。根据Futterman模型，在该模型中，介质吸收因子的频谱 $S\left(f\right)$ 可以表示为：

$S\left(f\right)=\exp \left[-\frac{\pi t}{Q}\left(f+iH\left(f\right)\right)\right]$ (6)

其中t为传播时间，f为频率，Q为品质因子， $H\left(f\right)$ 为频率f的希尔伯特变换。

在介质吸收因子的频谱表达式 $S\left(f\right)$ 中： $\exp \left(-\frac{\pi f}{Q}t\right)$ 表征地震波在传播中振幅的衰减； $\exp \left[-\frac{i\pi t}{Q}H\left(f\right)\right]$ 表征地震波在传播中相位的畸变。

在频域中，将吸收因子的频谱 $S\left(f\right)$ 与震源子波的频谱 $R\left(f\right)$ 相乘后再通过积分返回到时域则可以得到经过介质吸收衰减后的地震波 $x\left(t\right)$ ：

$x\left(t\right)=\frac{1}{2\pi }{\displaystyle \underset{0}{\overset{\infty }{\int }}R\left(f\right)S\left(f\right)\exp \left(i\omega t\right)\text{d}\omega }$ (7)

2.5. 反Q滤波

大地滤波的正过程为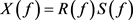：，式中： $R\left(f\right)$ 为地震子波； $S\left(f\right)$ 为吸收因子。反Q滤波的过程如下： $R\left(f\right)=X\left(f\right)S{\left(f\right)}^{-1}$，对 $R\left(f\right)$ 作傅里叶逆变换，可以得到时域子波 $r\left(t\right)$。式中： $S{\left(f\right)}^{-1}$ 为反Q滤波因子。

$S{\left(f\right)}^{-1}=\exp \left[\frac{\pi t}{Q}G\left(f\right)\right]$ (8)

3. 模拟资料处理

3.1. 大地滤波数值模拟

令震源为雷克子波，其频谱 $R\left(f\right)$ 为：

$R\left(f\right)=\frac{2}{\sqrt{\pi }}\frac{f^2}{f_m^2}\exp \left(-\frac{f^2}{f_m^2}\right)$ (9)

令式中的主频 $f_m=100\text{Hz}$，采样频率 $f_s=1000\text{Hz}$，频率 $f=1500\text{Hz}$。这就是正演中震源子波的初始参数，为标准的雷克子波。取品质因子Q为40，传播时间t为100 ms，可以正演出震源雷克子波经过大地滤波作用后的波形和频谱图(图1)。从图1中可以看到，经大地滤波作用后，在时域上表现为波形的振幅值减小，相位也发生畸变，不再是标准的雷克子波；在频域上表现为振幅谱高频部分的衰减要快于低频部分，即高频信息损失较多，导致其主频由高频端向低频端发生移动，频带带宽变窄。该正演结果符合地震波在地下介质中传播的客观规律。

3.2. 反Q滤波处理

补偿使用的Q值为已知的40，则得到反Q滤波后的波形和振幅谱(图2)。从图2中可以看到：经过反滤波处理后，时域上振幅值增大至与震源雷克子波保持一致，相位也恢复为原始形态；在频域上振幅谱大小与原始波形基本保持一致，损失的高频信息得以恢复，主频提高，频带变宽；因为此处使用的是无噪的理论模拟数据，并且品质因子为准确已知的真实Q值，反Q滤波的补偿效果理想。

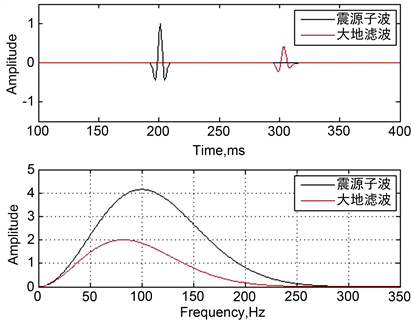
Figure 1. Amplitude spectrum and waveform after amplitude and phase attenuation (Q = 40, t = 100 ms)

图1. 振幅和相位发生衰减后的波形图和振幅谱(Q = 40, t = 100 ms)

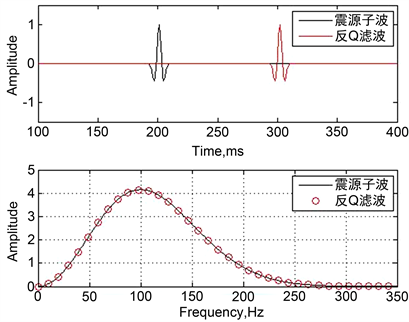
Figure 2. Waveform and amplitude spectrum after anti-Q compensation (Q = 40, t = 100 ms)

图2. 反Q补偿后的波形图和振幅谱(Q = 40, t = 100 ms)

4. 结论

本文模拟了大地滤波的正反过程。地震波在实际地层中传播时，会受到非完全弹性从而产生吸收衰减作用，在地震记录上表现为能量降低、波形畸变、分辨率的降低。对地震记录进行反Q滤波处理，时域上振幅值增大至与震源雷克子波保持一致，相位也恢复为原始形态；在频域上振幅谱大小与原始波形基本保持一致，损失的高频信息得以恢复，主频提高，频带变宽。

基金项目

本文为中国地质调查局科研项目(201100307)资助的成果。

NOTES

^*通讯作者。