基于熵值法的航路交叉点复杂度改善方案评价模型

An Evaluation Model for Improving the Complexity of Crossing Points Based on Entropy Method

摘要: 本文提出了一种基于熵值法的航路交叉点复杂度改善方案评价模型。首先，确定影响航路交叉点复杂度的主要因素，构建相应的评价指标体系；然后，对原始数据进行无量纲化处理，计算各指标的信息熵，确定它们的指标权重，据此计算出方案的综合评价得分。本文以HCH (黄城VOR)复杂交叉点的四种改善方案为例，验证该模型的正确性，辅助选择最佳改善方案。

Abstract: This paper presents an evaluation model for improving the complexity of crossing points based on entropy method. Firstly, the main factors affecting the complexity of crossing points are determined and the corresponding evaluation index system is constructed. Then, the original data is processed dimensionless, the information entropy of each index is calculated, the index weight is determined, and the comprehensive evaluation score of the scheme is calculated accordingly. In this paper, four improvement schemes for the complex intersection of HCH (Huangcheng VOR) are taken as examples to verify the correctness of the model and assist in selecting the best improvement scheme.

1. 引言

近年来，我国航空运输量增加迅猛，航路网结构与飞行流量之间的矛盾日益增加，这给空域运行带来了严峻考验。我国空域结构从几十年前初始形成一直沿用至今，多年来没有实质性改变，众多空中航路交叉点运行情况复杂，呈现交通流量大、飞行冲突多、运行效率低等特点。为提升安全裕度，通常采用流量控制手段加以缓解，但这可能降低空域总体运行效率。因此，空中航路交叉点的分析与优化已逐渐成为进一步提升空域通行能力和使用效率的重要方法。目前，可通过优化航路交叉点运行方式等策略来改善空域结构，常见方法包括空中环岛运行法、立交桥高度配置法和井字形交汇法三种方式。如何评价其优劣以选择最佳策略成为空域优化研究的方向之一。

目前，国内外相关文献主要归纳如下：王莉莉等 [1] 和朱承元等 [2] 定性分析了影响空中航路交叉点的复杂度涉及因素以及改善策略；李欢和王毅鹏 [3] 基于空域复杂度研究其扇区动态通行能力；吴哲等 [4] 基于空域结构复杂度对航路节点繁忙程度进行分级；赵立刚等 [5] 研究基于多目标进化的航路网络汇聚点设计方法；胡亚坤 [6] 探讨了基于航班流分布的航路交叉点复杂度分析；杜实等 [7] 探讨了基于扇区单元的航路交通流复杂度；王莉莉和贾铧霏 [8] 探讨了基于复杂度分析的空域扇区划分方法；高伟等 [9] 探讨了基于调速法的交叉航路空域复杂度。由上可知，现有研究主要集中在采用定量和定性相互结合的方法，分析空中航路交叉点的复杂度影响因素及其改善策略，并基于航路交叉点复杂度进行流量控制、扇区划分等空域管控，较少涉及对比不同改善策略的优缺点并筛选最佳方案。

优化航路交叉点运行方式的选取过程是一个由众多相互关联、相互制约的因素所构成的复杂系统 [10]。为尝试提升航路交叉点运行安全和效率，在研究国内外关于民航安全评价要素基础上，按照可量化、易测度的原则，基于熵值法的评价模型，从多维视角客观分析某航路交叉点在各个改善方案下的空域结构复杂性相关指标值的差异，据此对各个改善方案的好坏进行综合测度和评价，从而辅助筛选最佳方案。最后，通过选取典型繁忙航路交叉点的四种改善方案进行测试，从而验证本模型的有效性。

2. 评价指标体系构建

根据交叉点处运行特征，航路交叉点复杂度是指一定时间条件下用于评价指定航路交叉点运行难易程度的指标。同时，也可一定程度上反映该航路点处的管制工作负荷。但鉴于管制工作负荷的评估结果较依赖于管制员自身能力，主观性较强，本文暂不作考虑。交叉点复杂度根据点的空域结构和所处空域环境在建模度量方面具有明显差异，主要根据三个方面的影响因素进行分析：基本复杂度、动态复杂度及冲突复杂度(与冲突数量相关)。因此，可从冲突数量、基本复杂度、动态复杂度、冲突复杂度和交叉点复杂度五个方面，构建评价航路交叉点复杂度的指标体系，如表1所示。

Table 1. Index system

表1. 指标体系

3. 航路交叉点复杂度改善方案的评价模型构建过程

为了降低航路交叉点的复杂度，针对若干个改善方案，将信息熵法应用在优选最佳方案，主要思想是：用熵值来判断不同改善方案对于某个指标的离散程度，指标离散程度越大，该指标对综合评价的影响越大。

步骤1：构造评价矩阵

$A={\left(\begin{array}{ccc}{X}_{11}& \cdots & X_{1m}\\ ⋮& ⋮& ⋮\\ X_{n1}& \cdots & X_{nm}\end{array}\right)}_{n\times m}{X^{\prime }}_{ij}=\frac{X_{ij}-\min \left(X_{1j},X_{2j},\cdots ,X_{nj}\right)}{\max \left(X_{1j},X_{2j},\cdots ,X_{nj}\right)-\min \left(X_{1j},X_{2j},\cdots ,X_{nj}\right)}+1,i=1,2,\cdots ,n;j=1,2,\cdots ,m$

其中， $X_{ij}$ 为第i个改善方案第j个指标的数值。

步骤2：指标数据的标准化处理

针对成本型和效益型两类指标，基于信息熵法，计算任意方案的指标值与全部方案的最大和最小值之间偏离程度。

对效益型指标：

${X^{\prime }}_{ij}=\frac{X_{ij}-\min \left(X_{1j},X_{2j},\cdots ,X_{nj}\right)}{\max \left(X_{1j},X_{2j},\cdots ,X_{nj}\right)-\min \left(X_{1j},X_{2j},\cdots ,X_{nj}\right)}+1,i=1,2,\cdots ,n;j=1,2,\cdots ,m$

对于成本型指标：

${X^{\prime }}_{ij}=\frac{\max \left(X_{1j},X_{2j},\cdots ,X_{nj}\right)-X_{ij}}{\max \left(X_{1j},X_{2j},\cdots ,X_{nj}\right)-\min \left(X_{1j},X_{2j},\cdots ,X_{nj}\right)}+1,i=1,2,\cdots ,n;j=1,2,\cdots ,m$

步骤3：计算任意i改善方案的第j项指标占该指标的比重

$P_{ij}=\frac{X_{ij}}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{X}_{ij}}}\left(j=1,2,\cdots ,m\right)$

步骤4：计算第j项指标的熵值

$e_j=-k\ast {\displaystyle \underset{i=1}{\overset{n}{\sum }}{P}_{ij}\log \left(P_{ij}\right)}$ ，其中 $k>0$ ， $\ln$ 为自然对数， $e_j\ge 0$ 。式中常数k与样本数m有关，一般令

$k=1/\ln m$ ，则 $0\le e\le 1$

步骤5：计算第j项指标的差异系数

$g_j=1-e_j$

对于第j项指标，指标值 $X_{ij}$ 的差异越大，对方案评价的作用越大，熵值就越小。

步骤6：计算每个指标的权重，如下所示。

$W_j=\frac{g_j}{{\displaystyle \underset{j=1}{\overset{m}{\sum }}{g}_j}},j=1,2,\cdots ,m$

步骤7：计算任意改善方案的综合得分，如下所示。

$S_i={\displaystyle \underset{j=1}{\overset{m}{\sum }}{W}_j\ast P_{ij}}\left(j=1,2,\cdots ,n\right)$

4. 案例分析

以典型繁忙交叉点HCH(黄城VOR)的改善策略为例，如图1所示，该点为多条航路航线(包括W4、W5、H29、H30等)的汇聚交叉节点，结构复杂，运行繁忙。为降低复杂度，拟选用环岛运行和先行逐级汇聚两种策略，共设计四种方案，其基本情况如表2和图2~5所示。经过TAAM仿真后，其航路复杂度优化前后指标值如表3所示。

Figure 1. HCH route structure

图1. HCH航路结构

Table 2. The basic situation of the four operating schemes

表2. 四种运行方案的基本情况

Figure 2. Roundabout operation plan A

图2. 环岛运行方案A

Figure 3. Roundabout operation plan B

图3. 环岛运行方案B

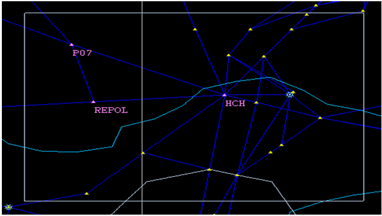
Figure 4. Priority level aggregation solution C

图4. 先行逐级汇聚方案C

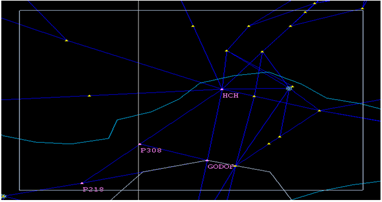
Figure 5. Priority level aggregation solution D

图5. 先行逐级汇聚方案D

Table 3. Comparison of index data before and after the four operation schemes

表3. 四种运行方案运行前后指标数据对比

对原始方案数据标准化后，计算任意指标的熵值、差异系数和权重如表4所示。从中可知：改高度复杂度和交叉点复杂度的影响作用一样，它们所占比重最大，冲突数量的影响作用最小。

Table 4. Entropy value, difference coefficient and weight of different indicators

表4. 不同指标的熵值、差异系数和权重

四个方案的综合评价分值如表5所示。分析可知：方案B的综合得分最高，方案C的综合得分最低，其排名依次为B-A-D-C。因此，以期降低HCH(黄城)交叉点复杂度，应考虑选择方案B。

Table 5. Comprehensive evaluation results of the plan

表5. 方案综合评价结果

5. 结论

本文的主要工作是如何比较改善航路交叉点复杂度的不同方案优缺点，并选择最佳方案。主要工作包括：1) 建立和完善影响航路交叉点复杂度的评价指标体系；2) 构建基于信息熵的方案选择与评价模型，给出了具体算法流程。最后，以HCH(黄城)复杂交叉点的四种改善方案为例，研究表明：1) 改高度复杂度和交叉点复杂度的影响作用一样，它们所占比重最大，冲突数量的影响作用最小；2) 方案B的综合得分最高，方案C的综合得分最低，其排名依次为B-A-D-C。

然而，本文模型假设影响不同改善方案在优化航路交叉点复杂度的各个指标值是静态，考虑交通流的动态、时变特性，它们是不确定的。因此，未来研究工作的重点是如何将信息熵法应用在评价与选择不确定性方案。