1. 引言
我国经济水平逐年增长,人民生活水平不断提高,旅游业的需求也逐渐旺盛起来,但是随着每年旅游人数增多,人多、车多造成旅游城市人满为患,景区停车困难,成了影响旅游业发展的障碍 [1]。因此,为满足人民日益增长的旅游需求、同时减少运力浪费,提高旅游企业经济效益,就要合理安排旅游车辆调度,以有效地节约旅游行业的运营成本、提高整个行业的服务质量和经营水平。
目前,国内外对于相关资源的调度研究逐步从静态调度研究转向动态调度研究。而动态调度方面的研究主要把重点放在算法的解决和改进方面,结合现实调度问题特点的研究不多。旅游大巴的调度作为对游客运输需求和旅游运力资源的一种平衡 [2]。旅游运输企业需要优先考虑的问题便是满足游客行程安排的车辆调度问题,这个问题是具体旅游线路规划当中最为重要的问题,关乎到旅游企业的服务质量以及运营成本。而运力调度优化模型及其求解算法是解决问题的关键。旅游运输企业在对游客需求以及游览计划进行充分了解之后,根据运力调度优化模型和算法计算出最优的行车路线,才能使得旅游车辆运力资源和游客运输需求得以匹配。
本文根据旅游车辆调度和组团游客出行的特点,构建带有时间窗约束的旅游大巴运力动态调度模型并设计相应算法。利用MATLAB进行仿真求解。
2. 问题分析
在传统的旅游车辆调度中,车辆在其规划好的行车路径中往往只被允许对同一个景点进行一次访问,而为了增加车辆的使用率,本文研究的情景将允许车辆在其规划好的行车路径中对于同一个景点进行多次的访问,这种对于同一个景点的多次访问的现象在一定程度上增加了建模与求解的难度。为此本文参照詹红鑫、王旭坪等的建模思路,根据客户需求的特征将客户进行拆分后设置虚拟结点来表示,这样便将复杂的多次访问问题通过虚拟结点转换为传统单次访问问题 [3]。本文的转换方式是根据旅行社的行程计划,对于接送游客的行车任务进行虚拟化处理,即将接送客的任务生成相互间距离已知,带有时间窗和服务时间的虚拟任务结点。这种转换方式有效地解决了多次访问同一景点的问题,简化了建模与求解的难度。
3. 旅游大巴运力动态调度模型构建及算法设计
3.1. 模型建立
3.1.1. 基本假设
对旅游调度做如下假设:
1) 旅游车辆场站、酒店、景点位置以及旅游团行程计划已知;
2) 每个任务只有一辆车服务一次且仅服务一次完成;
3) 车辆类型一致,车载容量和速度相同;
4) 任意两个任务之间均有通路;
5) 车辆行驶速度固定;
6) 每个任务的游客数都不超过车辆的车载容量;
7) 所有车辆都能按时到达第一个任务点。
3.1.2. 参数说明
:完整图;
V:行车任务节点集合,
;
C:任务集合;
A:弧组合;
n:任务数量;
m:实际使用车辆数;
:任务i结束点到任务j开始点距离;
:车辆从任务i终点到任务j起点的行驶时间;
:车辆在任务i的服务开始时间;
:车辆在任务i的服务结束时间;
:任务i开始的左时间窗;
:任务i开始的右时间窗;
:任务i所需的服务时间;
:惩罚函数;
:车辆k服务的任务数量;
决策变量:
表示的是车辆在第j个任务起点是否完成任务i的决策变量:车辆k从任务i终点到达任务j起点则
,否则
表示客户i由车辆k服务的决策变量:任务i由车辆k服务,则
,否则
;

在配送任务开始之前,初始路径的规划已经开始,此时平台对于当前旅游团的相关信息已经进行收集,根据这些信息进行制定初始方案。方案对行车距离和停车时间等都已经进行了最优安排,在没有接收到新的动态需求之前,这一方案会照常进行,直到新需求出现。
1) 目标函数建立
本文主要考虑以最少车辆最短路径完成所有接送任务且停车时间最少,因此以完成所有任务的时间成本T表示运输成本,如(3-1)所示:
(3-1)
2) 约束条件
(3-2)
(3-3)
(3-4)
(3-5)
(3-6)
(3-7)
(3-8)
(3-2)表示任何一个任务j的前继任务i唯一,该任务仅有一辆车服务一次;
(3-3)表示任何一个任务i的后继任务j唯一,该任务仅有一辆车服务一次;
(3-4) (3-5) (3-6)表示每辆车从场站出发服务过若干不重复后回到场站;
(3-7)表示任务 服务结束时间加上车辆从任务i到任务j的行驶时间一定要小于或等于客户服务开始的时间;
(3-8)表示建立时间窗函数。
第一阶段通过对获得的旅客信息的分析和处理,进行了初始的路径规划,车辆按照初始的路径行驶完成任务直到新的任务出现。如果有了新的需求发送到调度中心,为了满足新的任务需求,第一阶段初始路径需要被优化调整,调度中心就会进行重新的路径规划。
假设在
时刻,出现f个新的任务,设第一阶段派出
辆车,此时第一阶段已经被完成的任务为h个。目标函数:
(3-9)
流程图如下图1:
针对旅游大巴运力调度问题的求解算法主要是现代启发式的优化算法 [4] [5] [6] [7] [8]。本文所设计的调度方法的第一个阶段是对初始路径的静态优化,采用遗传算法对模型进行求解,给出一个最初的路径静态优化方案。随后在车辆服务运行的过程当中,如果动态需求产生了,本方案会选择大邻域搜索算法,利用大邻域搜索算法的破坏与修复思想进行局部寻优,将新的任务插入静态调度行车计划中,更新路径继续采用遗传算法进行适应度值的计算跟判别,选择最优的插入位置进而得出最优的运输路径,以此来对上一阶段的初始路径进行重新的规划。算法整体设计如图2。
4. 算例分析
本文以桂林市秀峰区、象山区和七星区几处著名景点为实例研究对象,进行旅游大巴运力动态调度实例仿真研究。桂林市秀峰区、象山区和七星区道路网完善,车辆可达性较好,内部景区酒店众多,如大瀑布酒店、环球大酒店、日月双塔文化公园、穿山公园、七星公园等都会产生的大量旅游出行需求,这些条件使得该区域内具备了开展旅游大巴运力动态调度的外部条件。所选区域如图3所示。
现有8个相同规模的旅游团,一天内产生有8条出行链,根据出行需求,旅行社和旅游运输企业最多提供8辆旅游大巴来完成运输服务。假设8台车辆均符合统一标准,即每台车的运载能力满足运输需求;车辆的最大行驶距离能够完成一天的行程任务;车辆行驶速度均匀;各条道路状态相同,任务点间的距离为实际道路距离。8个团的一天游览计划如下:
1) 酒店1–七星公园–南溪山公园–西山公园–酒店1;
2) 酒店1–独秀峰王城景区–穿山公园–桂林园林植物园–酒店1;
3) 酒店1–西山公园–桂林园林植物园–穿山公园–酒店1;
4) 酒店2–日月双塔文化公园–南溪山公园–酒店2;
5) 酒店2–西山公园–日月双塔文化公园–南溪山公园–七星公园–酒店2;
6) 酒店2–桂林园林植物园–西山公园–独秀峰王城景区–日月双塔文化公园–酒店2;
7) 酒店2–南溪山公园–日月双塔文化公园–酒店2;
8) 酒店3–日月双塔文化公园–独秀峰王城景区–桂林园林植物园–酒店3。
将8个旅游团的计划分解成了32个行车任务后,各任务的开始时间
与结束时间时间
如表1所示:
未进行运力静态调度调整之前,所有车辆都只负责一个指定旅游团的运输任务,因此,因调度产生的行驶距离为0 km即调度时间为0 min,停车总时长1290 min。旅行社和旅游运输公司原始的派车计划如表2所示:
本章设计的遗传算法采用MATLAB R2014b实现,实验机器为Intel cure i5处理器,2.67GHz的计算机。为了计算时间,车辆速度设置为匀速且行驶速度
。遗传算法设定种群规模
,交叉概率
,变异概率
,最大进化代数
。仿真实验中主要采取车辆为了完成所有任务而增加的调度行驶时间和在景区停车场停车等待时间评价指标来进行验证。实验结果如表3所示:
算法耗时168.7 s。从表中我们可以看出来经过优化调度后,在满足所有约束条件的情况下,完成所有订单的运输任务所使用车辆数由原来的8辆减少为优化后的5辆车。静态调度后,停车时间减少653.4 min,车辆利用率提升60%;静态调度后,减少了3台车的使用,3台车一天的成本约为1200元;而因静态调度所增加的调度时间为173.4 min,增加行驶距离57.8 km,按百公里30 L油耗计算,柴油价格6.06元/L,增加成本约为104.04元;总计,一天节约成本为1095.6元。优化前后路径图如图4、图5所示:
为了使设计的算法效率得到验证,本文对于染色体当代最优解和遗传代数之间的关系作了算法收敛状况图,如图6所示。从图中可以看出,算法前期搜索能力较强,在10代已经开始收敛,后期又能保留种群的优良基因,至30代已趋于稳定,可见算法效率满足设计要求。
在时刻8:30、9:30、10:00分别插入动态任务33王城–南溪山公园;34穿山–南溪山公园;35植物园–南溪山公园。任务的时间窗如表4:
通过大邻域搜索优化后的动态调度结果如表5所示:

Table 5. Dynamic scheduling results
表5. 动态调度结果
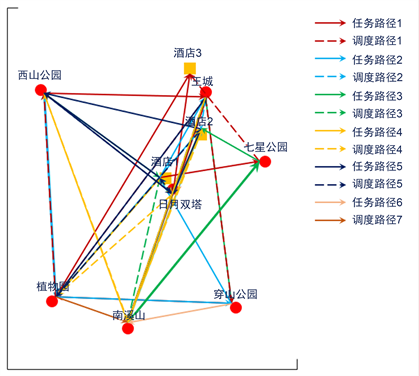
Figure 7. Dynamic scheduling path graph
图7. 动态调度路径图
通过动态调度将新增任务33插入到静态调度路径4中,任务34和任务35因不满足约束条件,无法插入静态调度计划中,故分别增加路径6和路径7,即增派两辆车使新增任务得以完成。相比常规调度需要增派3台车,共11台车,动态调度只增加2台车,共7台车,停车等待652.8 min,车辆利用率提高57%,车辆维护成本减少1600元;调度时间187.2 min,调度距离62.4 km,调度成本113.4元,合计减少成本1486.6元。动态调度后路径如图7所示。
5. 结论
在旅游运输行业的发展过程中,相关企业所面临的核心问题即为运力调度问题,所以对与运力的合理安排从各个角度来说都比较具有现实的意义。因此对于运输路线的合理规划和对车辆的合理调度都能够使得企业实现资源的优化利用和合理配置,在降低资源浪费的同时使得车辆利用率得以提升。此外,合理的运力调度能够使得旅游运输企业获得更高的收益,以降低成本的方式来控制企业的支出,并且提升服务质量。从而使得其自身的核心竞争力得以加强。在结合时代需求的情况下本文构建起了一个带时间窗约束的旅游大巴运力动态调度优化模型,从而使得旅游运输行业能够实现成本最小并且增强客户满意度的需求。本文所得出的结论如下:
1) 在本文当中,研究过程对于旅游大巴的运营特性和运输特性进行了充分的考虑,针对这一过程当中的随机性和动态性的特性,这一模型实现了对模型的优化,使其能够在满足旅客需求的情况下使得运输成本降到最低。
2) 此外本文还设计了一个两阶段的算法的动态模型,用来解决多目标的复杂问题,这一模型采用的算法是大邻域搜索算法,用来对新动态需求进行解决,而遗传算法则用来解决静态初始路径的优化问题。
3) 本文主要将理论的算法和模型配合实际案例来进行分析,从而使得旅游运输企业能够实现运力调度的科学有效,在保障服务质量确保旅客满意的情形下使得旅游大巴的运输成本降低,提升其利用率,同时也说明了模型的建立更加符合实际意义。