基于Creo的液力变矩器参数化设计

Creo-Based Parametric Design of a Torque Converter

摘要: 提出了一种液力变矩器参数化设计方法，将整个参数化设计过程集成在Creo三维设计软件中完成，大幅缩短了液力变矩器的改型设计周期。首先应用三段圆弧法完成循环圆的参数化设计，然后分别阐述了泵轮、涡轮和导轮的参数化设计过程，并最终构建了液力变矩器参数化几何模型和流道模型。应用同样的仿真策略对原始模型和参数化设计模型进行三维流场仿真计算，结果表明，参数化设计前后的性能仿真结果几乎完全一致，验证了液力变矩器参数化方法的正确性。该方法实现了液力变矩器的快速改型，为进一步性能优化设计提供了模型基础。

Abstract: A parametric design method of a torque converter was proposed, and the design cycle was greatly shortened by integrating the whole parametric design process into Creo design software. The three-segment arc method was applied first to complete the parametric design of torus, and then the parametric design process of pump, turbine and stator was introduced respectively. In the end, the parametric geometric model and flow channel model of the torque converter were constructed. The three-dimensional flow field of original model and parametric design model were calculated by using the same simulation strategy. The results show that performance calculation results before and after parametric design are almost identical, which verifies the correctness of the parametric design method. The proposed method realizes the quick modification of a torque converter, and provides model basis for further performance optimal design.

1. 引言

液力变矩器的设计主要包括循环圆的设计和叶栅系统的设计。循环圆设计应用较为普遍的方法为三圆弧法，循环圆外环由三段相切圆弧组成，根据循环圆中间流线两侧过流截面积相等的原则，确定中间流线和内环的形状和位置。而其他循环圆设计方法的相关研究文献 [1] [2] [3] 相对较少。叶栅系统的设计是液力变矩器设计的重点和难点。文献 [4] 利用贝塞尔曲线进行液力变矩器叶片骨线和厚度的构造，建立了叶栅系统参数化设计模型，并编制了叶栅系统造型软件，实现了液力变矩器叶栅系统的参数化建模。文献 [5] 应用儒科夫斯基型线进行液力变矩器导轮叶片造型研究，通过变换并加入尾部加厚项处理，使儒科夫斯基型线适应液力变矩器导轮叶片设计需要，并编制了参数化儒科夫斯基型线导轮叶片设计程序。文献 [6] 基于非均匀有理B样条(NURBS)研究了液力变矩器叶栅系统改型设计方法，通过调整NURBS曲线的控制点以及各控制点权重值，实现叶片角变化规律的调整，并构建了液力变矩器改型平台。叶栅系统为空间三维结构，主要是通过编程或基于编程的设计平台完成参数化设计。而目前液力变矩器基于编程的参数化设计通常需要借助Matlab等第三方软件，然后将生成的模型特征导入到三维设计软件中。该方法存在着一定的不足，一方面几何模型在软件之间传递有可能造成模型的失真，另一方面，每一次模型的传递都意味着设计周期的增加。

本文提出了一种液力变矩器参数化设计方法，将整个参数化过程集成到Creo三维设计软件中，液力变矩器改型时能够实现模型的“一键更新”，大大提高了改型设计效率。

2. 保角变换原理

液力变矩器叶栅系统为复杂的空间曲面结构，叶片的真实长度、厚度和角度不易直接表达，为了方便的对叶片各设计参数进行定义，一般采用保角变换的方法，将空间曲线(或曲面)展开在平面上，而倾斜角度保持相等。图1为保角变换原理图，图中，(a)和(b)分别为设计曲线的轴面图和正视图，(c)为设计曲线绕轴心线旋转而成的空间曲面，(d)为用以表达设计参数的设计平面。对空间曲面，分别作垂直于轴心线和通过轴心线的平面簇，两平面簇与空间曲面的交线形成很多正交网格。正交网格中，由 $d{l}_1$， $d{n}_1$， $d{s}_1$ 组成的微小曲面三角形与设计平面上由 $d{l}_2$， $d{n}_2$， $d{s}_2$ 组成的微小三角形相似则可保持变换后倾斜角与叶片的倾斜角相等。由于设计曲线各点的半径是变化的，因而设计平面曲线上每段与其真实长度的比例也是变化的，为了保证设计平面曲线的长度为叶片空间曲线的真实长度，采用多圆柱等角射影法，此时空间曲面微小曲面三角形与设计平面微小三角形存在以下关系：

$\{\begin{array}{l}\text{d}{l}_1=\text{d}{l}_2\\ \text{d}{n}_1=\text{d}{n}_2\\ \text{d}{s}_1=\text{d}{s}_2\end{array}$ (1)

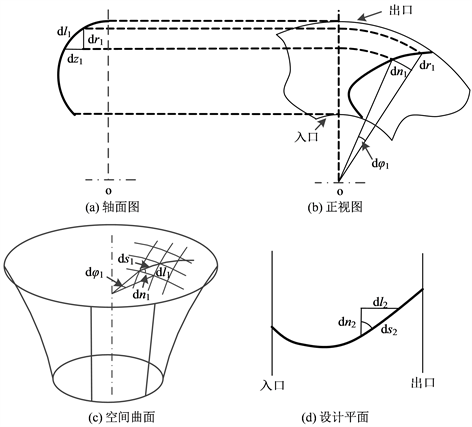
Figure 1. Schematic diagram of conformal transformation

图1. 保角变换原理图

3. 参数化设计

3.1. 循环圆参数化设计

基于Creo三维设计软件，采用三圆弧方法对液力变矩器循环圆进行正向参数化设计，首先应用有效直径D、循环圆宽度W和第一、三段圆弧半径可以确定循环圆的外环。根据过流截面面积近似相等的原则，输入相对截面积 $f_a$ 进一步确定循环圆的中间流线和内环，初步参数化设计的液力变矩器循环圆内外环如图2所示。

Figure 2. Preliminary parametric design of torus

图2. 循环圆内外环初步参数化设计

基于液力变矩器初步参数化设计循环圆，结合泵轮、涡轮的进出口位置参数以及循环圆导轮部分的相关尺寸参数可以得到理论循环圆的参数化设计模型。最后对循环圆内环进行几何修正并对修正部分实现参数化，如图3所示。

Figure 3. Parametric design of practical torus

图3. 实际循环圆参数化设计

3.2. 泵轮参数化设计

泵轮正向参数化设计的重点和难点是泵轮叶片的参数化设计，而泵轮叶片设计的核心是保角变换的实现过程。本文液力变矩器正向参数化设计过程是在Creo三维设计软件中完成的，将保角变换的过程集成在设计软件中。对于泵轮，首先需要对叶片内外环二维设计曲线进行数学关系描述，对于目标液力变矩器，泵轮叶片内外环二维设计曲线是由一段二次曲线和三段直线段构成，设计曲线示意图如图4所示。

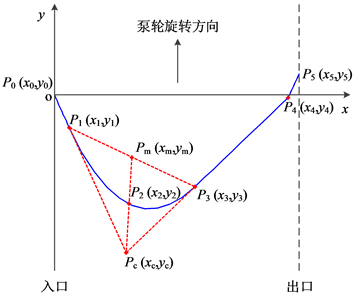
Figure 4. Two-dimensional design curve of core and shell in pump blade

图4. 泵轮叶片内外环二维设计曲线示意图

图4中二维设计曲线起始点分别为 $P_0\left(x_0,y_0\right)$ 和 $P_5\left(x_5,y_5\right)$， $P_1\left(x_1,y_1\right)$ 和 $P_3\left(x_3,y_3\right)$ 分别为二次曲线与入口端直线段和中间直线段的切点， $P_4\left(x_4,y_4\right)$ 为中间直线段与出口端直线段的交点， $P_c\left(x_c,y_c\right)$ 为二次曲线两端切线的交点， $P_m\left(x_m,y_m\right)$ 为 $P_1{P}_3$ 线段的中点， $P_2\left(x_2,y_2\right)$ 为 $P_m{P}_c$ 与二维设计曲线的交点。横坐标代表泵轮叶片内外环循环圆弦长方向，从入口端指向出口端。因此， $x_5$ 的大小等于泵轮内外环循环圆的长度，可以在三维设计软件中直接测量得到。三段直线段的斜率可以通过泵轮叶片内外环叶片角变化规律求得，对于外环有

$\{\begin{array}{l}{k}_1=\tan \left({90}^{\circ }-{\beta }_{PI}\text{\_}O\right)\\ k_2=\tan \left({90}^{\circ }-{\beta }_{PM}\text{\_}O\right)\\ k_3=\tan \left({90}^{\circ }-{\beta }_{PO}\text{\_}O\right)\end{array}$ (2)

式中， $k_1$， $k_2$， $k_3$ 分别为入口端直线段 $P_0{P}_1$，中间直线段 $P_3{P}_4$ 和出口端直线段 $P_4{P}_5$ 的斜率。

同样的，对于泵轮叶片内环有

$\{\begin{array}{l}{k}_1=\tan \left({90}^{\circ }-{\beta }_{PI}\text{\_}I\right)\\ k_2=\tan \left({90}^{\circ }-{\beta }_{PM}\text{\_}I\right)\\ k_3=\tan \left({90}^{\circ }-{\beta }_{PO}\text{\_}I\right)\end{array}$ (3)

坐标值 $x_1$ 、 $x_3$ 和 $x_4$ 可以分别通过泵轮叶片内外环位置参数 $a_{P1}\_I/a_{P1}\_O$ 、 $a_{P2}\_I/a_{P2}\_O$ 和 $a_{P3}\_I/a_{P3}\_O$ 与内外环循环圆长度相乘计算求得，坐标值 $y_5$ 为泵轮叶片内外环二维设计曲线出口周向偏移 $l_P$，可以通过逆向设计二维设计拟合曲线测量求得。线段 $P_0{P}_1$ 的表达式为

$y=k_{1}x,0\le x\le x_1$ (4)

线段 $P_4{P}_5$ 的表达式为

$y=k_3\left(x-x_5\right)+y_5,x_4\le x\le x_5$ (5)

由式(5)可以求出 $P_4$ 点坐标，线段 $P_3{P}_4$ 的表达式为

$y=k_2\left(x-x_4\right)+y_4,x_3\le x\le x_4$ (6)

由式(6)求得 $P_3$ 点坐标，式(4)和式(6)求得两线交点 $P_c$ 坐标， $P_m$ 点坐标为

$\{\begin{array}{l}{x}_m=\frac{x_1+x_3}{2}\\ y_m=\frac{y_1+y_3}{2}\end{array}$ (7)

引入圆锥曲线参数 $f_c$，则 $P_2$ 点坐标可由下式求得

$\{\begin{array}{l}{x}_2=x_m+\left(x_c-x_m\right)\cdot f_c\\ y_2=y_m+\left(y_c-y_m\right)\cdot f_c\end{array}$ (8)

二次曲线 $P_1{P}_3$ 的一般表达式为

$\begin{array}{l}{A}^{\prime }{x}^2+B^{\prime }{y}^2+C^{\prime }x+D^{\prime }y+E^{\prime }xy+F^{\prime }=0,\\ x_1\le x\le x_3\end{array}$ (9)

式中， $A^{\prime },B^{\prime },C^{\prime },D^{\prime },E^{\prime },F^{\prime }$ 为未知系数。考虑到二次曲线的唯一性，取 $D^{\prime }$ 值为1，则式(9)可变为

$\begin{array}{l}{A}^{\prime }{x}^2+B^{\prime }{y}^2+C^{\prime }x+y+E^{\prime }xy+F^{\prime }=0,\\ x_1\le x\le x_3\end{array}$ (10)

二次曲线过 $P_1$， $P_2$， $P_3$ 三坐标点，且在两端点的切线斜率已知，故式中未知系数可由下式求得

$\{\begin{array}{l}{A}^{\prime }{x}_1^2+B^{\prime }{y}_1^2+C^{\prime }{x}_1+y_1+E^{\prime }{x}_1{y}_1+F^{\prime }=0\\ A^{\prime }{x}_2^2+B^{\prime }{y}_2^2+C^{\prime }{x}_2+y_2+E^{\prime }{x}_2{y}_2+F^{\prime }=0\\ A^{\prime }{x}_3^2+B^{\prime }{y}_3^2+C^{\prime }{x}_3+y_3+E^{\prime }{x}_3{y}_3+F^{\prime }=0\\ \left(2B^{\prime }{y}_1+E^{\prime }{x}_1+1\right)k_1+2A^{\prime }{x}_1+E^{\prime }{y}_1+C^{\prime }=0\\ \left(2B^{\prime }{y}_3+E^{\prime }{x}_3+1\right)k_2+2A^{\prime }{x}_3+E^{\prime }{y}_3+C^{\prime }=0\end{array}$ (11)

应用目标液力变矩器泵轮叶片设计参数作为输入求解二维设计曲线方程系数，根据确定的方程构建泵轮叶片内外环二维设计曲线，该正向设计曲线与实际曲线对比结果如图5所示。可以看出，泵轮叶片内环和外环正向设计的二维设计曲线与实际曲线基本完全吻合，说明了泵轮叶片内外环二维设计曲线正向参数化设计方法的正确性。

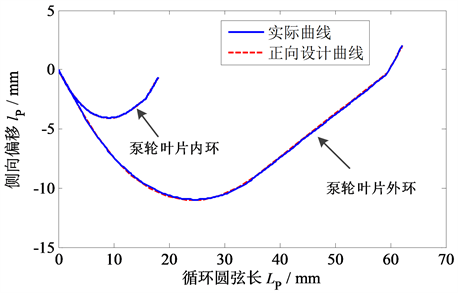
Figure 5. Comparison of two-dimensional parametric design curve and actual curve for pump core and shell

图5. 泵轮叶片内外环正向参数化二维设计曲线与实际曲线对比

已知泵轮叶片内外环对应的循环圆曲线和二维设计曲线，通过保角变换可以分别求得泵轮叶片内外环三维空间曲线，该参数化过程以编程的形式集成在三维设计软件中。目标液力变矩器泵轮叶片为等厚直叶片，输入叶片内外环偏转角和叶片厚度可以确定泵轮叶片几何模型，输入叶片数进一步确定泵轮叶栅系统，泵轮参数化设计过程如图6所示。

3.3. 涡轮参数化设计

与泵轮叶片相比，涡轮叶片更为扭曲，对于目标液力变矩器，涡轮叶片内外环二维设计曲线是由一段二次曲线和相邻的两段直线段构成，设计曲线示意图如图7所示。

图7中 ${P^{\prime }}_0\left(x_0,y_0\right)$ 和 ${P^{\prime }}_4\left(x_4,y_4\right)$ 分别为二维设计曲线起始点， ${P^{\prime }}_1\left(x_1,y_1\right)$ 和 ${P^{\prime }}_3\left(x_3,y_3\right)$ 分别为二次曲线与入口端直线段和出口端直线段的相切点， ${P^{\prime }}_{\text{c}}\left(x_{\text{c}},y_{\text{c}}\right)$ 为二次曲线两端切线的交点， ${P^{\prime }}_{\text{m}}\left(x_{\text{m}},y_{\text{m}}\right)$ 为 ${P^{\prime }}_1{P^{\prime }}_3$ 线段的中点， ${P^{\prime }}_2\left(x_2,y_2\right)$ 为 ${P^{\prime }}_{\text{m}}{P^{\prime }}_{\text{c}}$ 与二维设计曲线的交点。横坐标代表涡轮叶片内外环循环圆弦长方向，从入口端指向出口端。与泵轮叶片相比，涡轮叶片没有出口折弯，因此涡轮内外环的二次设计曲线只有两段直线段。但是涡轮整个二维设计曲线数学表达式的计算方法与泵轮是相同的，或者可以认为是泵轮二维设计曲线表达式的一种特殊情况(中间直线段与出口端直线段交点位置参数为1)，因此，对涡轮叶片内外环二维设计曲线表达式计算方法不再具体描述。图8为涡轮叶片内外环正向参数化二维设计曲线与实际曲线拟合结果，可以看出，两者具有较高的吻合度。

Figure 6. Parametric design process of pump

图6. 泵轮参数化设计过程

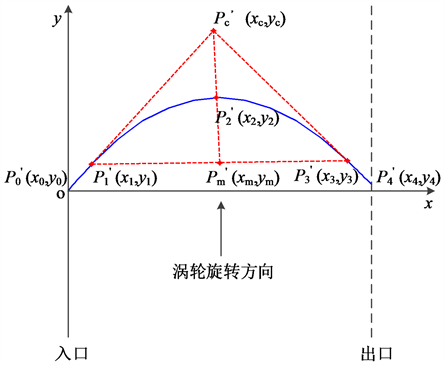
Figure 7. Two-dimensional design curve of core and shell in turbine blade

图7. 涡轮叶片内外环二维设计曲线示意图

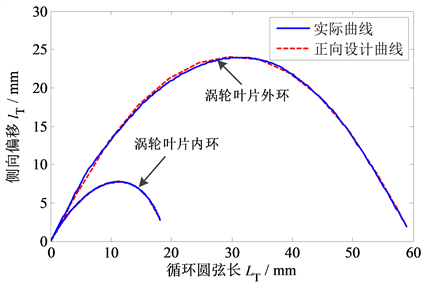
Figure 8. Comparison of two-dimensional parametric design curve and actual curve for turbine core and shell

图8. 涡轮叶片内外环正向参数化二维设计曲线与实际曲线对比

已知涡轮叶片内外环对应的循环圆曲线和二维设计曲线，通过保角变换可以分别求得涡轮叶片内外环三维空间曲线，该参数化过程同样以编程的形式集成在三维设计软件中。目标液力变矩器涡轮叶片为等厚直叶片，输入叶片内外环偏转角和叶片厚度可以确定涡轮叶片几何模型，输入叶片数进一步确定涡轮轮叶栅系统，涡轮参数化设计过程如图9所示。

Figure 9. Parametric design process of turbine

图9. 涡轮参数化设计过程

3.4. 导轮参数化设计

导轮叶片参数化的设计首先需要完成叶片内外环厚度轮廓二维设计曲线的参数化设计，该过程涉及到中弧线参数化和叶片厚度沿中弧线的变化规律曲线参数化。目标液力变矩器导轮叶片内外环厚度轮廓中弧线是由入口端的一段二次曲线和与之相切的出口端的一段直线段构成。与泵轮和涡轮叶片不同，导轮叶片厚度轮廓中弧线无需进行数学表达式描述，在三维设计软件中可以直接完成参数化设计。确定导轮叶片厚度轮廓中弧线需要的设计参数包括导轮叶片内外环进口角，导轮叶片内外环出口角，导轮叶片内外环圆锥曲线参数，导轮叶片内外环中弧线二次曲线与出口端直线段切点位置参数和导轮叶片中弧线内外环周向偏移。导轮叶片内外环轴向尺寸与液力变矩器实际循环圆导轮部分内外环轴向尺寸是一致的，因此，在实际循环圆确定后，该尺寸即为已知尺寸。导轮叶片内外环厚度轮廓中弧线参数化设计示意图如图10所示。

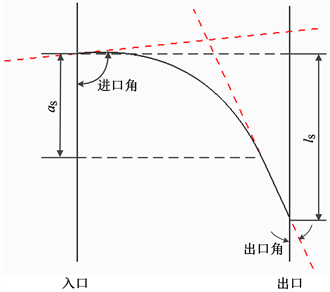
Figure 10. Parametric design diagram of middle arc for blade thickness profile in stator core and shell

图10. 导轮叶片内外环厚度轮廓中弧线参数化设计示意图

不同液力变矩器导轮叶片厚度沿中弧线的变化规律不尽相同，本文选用目标液力变矩器的设计参数对导轮叶片内外环厚度变化规律进行参数化设计，变化规律曲线示意图如图11所示。

(a) 外环(b) 内环

Figure 11. Variation of blade thickness in stator core and shell along middle arc

图11. 导轮叶片内外环厚度沿中弧线变化规律示意图

导轮叶片内外环厚度轮廓二维设计曲线确定后，通过保角变换即可得到导轮叶片内外环厚度轮廓三维几何参数化模型。目标液力变矩器的导轮叶片为直叶片，根据导轮叶片内外环偏转角即可确定导轮叶片，已知导轮叶片数进一步完成导轮叶栅系统的参数化设计。导轮参数化模型设计过程如图12所示。

Figure 12. Parametric design process of stator

图12. 导轮参数化模型设计过程

3.5. 流道模型参数化设计

泵轮、涡轮和导轮参数化设计完成后通过装配即可完成整个液力变矩器的参数化设计，液力变矩器参数化几何模型如图13(a)所示。对液力变矩器进行三维流场仿真计算分析需要建立流道模型，应用同样的方法对流道模型进行参数化设计，完成的全流道模型如图13(b)所示。

(a) 几何模型 (b) 全流道模型

Figure 13. Parametric geometric and whole channel models of the torque converter

图13. 液力变矩器参数化几何模型和全流道模型

液力变矩器为旋转机械，内部传动油流动呈周期变化，为了节省计算时间和计算机资源，在三维仿真计算时往往选取单流道模型作为计算基础模型，液力变矩器单流道参数化模型如图14所示。

Figure 14. Single channel parametric model of the torque converter

图14. 液力变矩器单流道参数化模型

4. 模型仿真验证

4.1. 网格划分

通过目标液力变矩器参数化模型与原始模型几何对比已经初步验证了不同部件参数化模型的正确性，进一步基于三维流场仿真对整个参数化模型进行正确性验证。首先建立计算模型，对流道模型进行网格划分。液力变矩器流道模型有全流道模型和单流道模型，选用已完成参数化的单流道模型完成流道模型的网格划分。网格划分过程中选用非结构化网格和多面体网格技术，非结构化网格方法生成网格过程中人工参与的工作量较小，能够较大的提高网格划分的效率，而多面体网格在促进计算收敛及精度方面都有很好的优势，单流道计算模型如图15所示。液力变矩器三工作轮计算模型网格基础尺寸均为1 mm，泵轮单元网格数为47,952，节点数为234,500；导轮单元网格数为65,210，节点数为237,167；涡轮单元网格数为47,234，节点数为226,840。

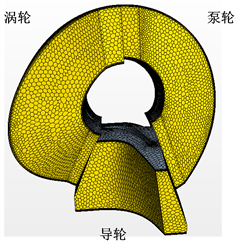
Figure 15. Computational model of single channel

图15. 单流道计算模型

4.2. 仿真计算

采用同样的仿真策略分别对原始单流道模型和参数化单流道模型进行三维流场仿真计算，计算结果如图16所示。从图中可以看出，参数化设计模型的液力性能曲线与原始模型的液力性能曲线几乎完全吻合，进一步说明本文提出的参数化设计方法的正确性，该参数化设计模型可以代替原始模型进行后续的研究。

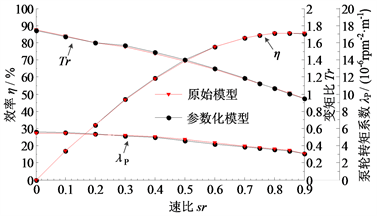
Figure 16. Comparison of hydraulic performance between parametric model and original model

图16. 参数化模型与原始模型液力性能对比

5. 结论

1) 提出了一种液力变矩器正向参数化设计方法，将整个参数化设计过程集成在三维设计软件中，避开了第三方软件的介入，极大地提高了改型设计效率。

2) 完成液力变矩器全流道和单流道模型的参数化设计，为三维流场仿真计算提供了模型基础。

3) 应用同样的三维流场仿真策略分别对液力变矩器原始模型和参数化设计模型进行仿真计算，对比结果说明了参数化设计方法的正确性。