镀铝件结构与镀铝层膜厚的关系研究

Research on the Relationship of the Aluminum Plates and the Thickness of Aluminum Coating

摘要: 本文针对汽车车灯镀铝工艺，研究了镀铝件结构与镀铝层膜厚之间的关系这一问题。首先对长方体、楔形、锥形以及梯形这四种结构的模型，做了膜厚测试实验，然后引入立体角的概念表征几何体的结构特征，通过利用CATIA软件计算出对应的膜厚测试点的立体角，利用数据分析软件MINITAB，提出了膜厚与结构的关系表达式。最后，通过数值算例验证了本文结论的有效性。

Abstract: This paper investigates the relationship between the structure of aluminum plates and the thick-ness of aluminum coating for automobile lamps. Firstly, four models with different structure are adopted to test the film thickness. Then, on the basis of the solid angle method, the structural fea-tures of geometry are described. And then, based on the CTAIA and MINITAB, the expression of film thickness and structure is given. Finally, the numerical simulation example illustrates the ef-fectiveness of the results presented in this paper.

1. 引言

汽车车灯不仅仅是安全件、法规件，也是汽车的一个重要的外观件。在汽车产业飞速发展的这几十年，汽车工业对车灯的要求也越来越严格。车灯的整体设计主要从车灯的结构、光学和材料等方面综合考虑，常规情况下，车灯注塑成型以后，使用镀铝工艺提高表面反射率。真空蒸发镀铝是常用的镀铝手段，最早于1933年被提出 [1]。之后在七十年代被应用在香烟的内衬包装等方面，主要是镀铝纸的研制等工艺应用 [2]。随着汽车行业猛速发展，镀铝工艺在车灯上的应用越来越频繁 [3]。车灯的反射镜、饰圈等镀铝零件为了做到配光和美观的双重要求通常曲面结构设计的较为复杂，但是复杂的曲面结构设计会影响镀铝层的均匀性。因此，研究镀铝件的结构与镀层膜厚的关系对车灯的设计有着重要的应用价值。

本文针对四种不同结构的镀铝零件，证明膜层厚度与立体角存在关系，并基于MINITAB软件，给出了任意结构的镀铝零件，膜层厚度的设计方案。并通过对EBO A SH后组合灯2壳体的膜层厚度计算，验证本文结果的有效性。

2. 镀铝膜层厚度测试

镀铝膜层的厚度直接影响镀铝膜质量，不同结构的零件，膜层厚度均匀性难以保证。为了验证镀铝膜层厚度与镀铝件结构的关系，本文选择验证的镀铝件模型有四种，见图1：

Figure 1. Four models of aluminum plates

图1. 四种镀铝件模型

试验中，使用的镀铝设备及相关技术参数见图2。

2.1. 测厚仪

铝层测试试验中，选用超薄蒸发金属膜层测厚仪(见下图)测试镀件膜层厚度。该试验中，设置的技术参数见下表1：

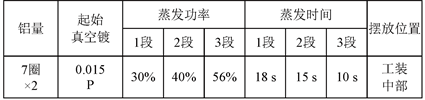
Figure 2. Parameters of aluminizing equipment

图2. 镀铝设备参数

Table 1. Parameters of thickness gauge

表1. 测厚仪参数

2.2. 测试方法

放置于工装上的待镀铝零件模型，先对其模型样板进行编号。以正对镀铝机的开口方向为观察方向，依次给模型底面，模型上面，模型下面，模型左面，模型右面编号：序号1，序号2，序号3，序号4以及序号5。

再将编号完成的模型拆开，在镀铝样板上划10 mm × 10 mm的正方形，测试位置在正方形中间，按箭头方向进行测试，每个正方形取一个膜厚值，直到测试不出数值为止，见图3。

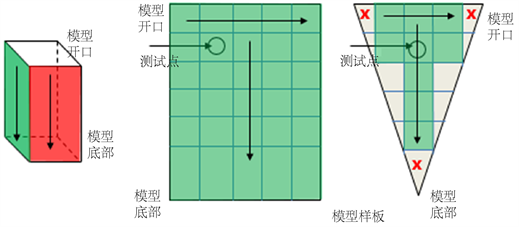
Figure 3. Reading the thickness of aluminum coating

图3. 读取镀铝层厚度

3. 立体角的计算

立体角是对应于平面几何中的平面角的概念在三维空间的类推，用以描述一个物体对特定点的三维空间的角度。通过引入立体角的概念，刻画复杂结构的镀铝件在三维空间中的几何特征。

应用catia相关软件测量出四面体模型0-ABC (见图4)的相关平面角∠AOB，∠AOC，∠BOC。

Figure 4. Tetrahedral model O-ABC

图4. 四面体模型O-ABC

根据测得的平面角按照下列公式计算立体角：

$\Omega =4\arctan \sqrt{\tan \left(\frac{s}{2}\right)\tan \left(\frac{s-\alpha }{2}\right)\tan \left(\frac{s-\beta }{2}\right)\tan \left(\frac{s-\gamma }{2}\right)}$ (1)

其中， $s=\alpha +\beta +\gamma$， $\alpha$ 表示∠BOC的度数， $\beta$ 表示∠AOC的度数， $\gamma$ 表示∠BOC的度数，这里立体角Ω是观察点O面向开口平面ABC的角度，值得注意的是这里的0点的观察面是一个三角形，对于观察面是四边形的五面体模型的立体角的计算方法，可通过分割五面体为两个四面体，计算两个四面体的立体角来获取五面体的立体角。

对于五面体模型O-ABCD (见图5)，计算观察点面向开口平面ABCD的立体角方法如下：

Figure 5. Pentahedral model O-ABCD

图5. 五面体模型O-ABCD

连接BD (AC亦可)，先根据公式(1)计算四面体O-ABD的立体角 ${\Omega }_1$，再根据公式(1)计算四面体O-BCD的立体角 ${\Omega }_2$，则五面体O-ABCD的立体角：

$\Omega ={\Omega }_1+{\Omega }_2$

4. 实验结果及分析

在模型中用“x”标识出膜厚测试位置，使用测厚仪测试出标识位置的膜层厚度，再利用CATIA软件测量相关平面角，计算出每个标识位置观察开口平面的立体角(见图6)。

Figure 6. Solid angle

图6. 立体角

4.1. 确定膜厚与立体角的实验数据

1、长方形模型试验数据如下表2。

Table 2. Rectagular model test data

表2. 长方形模型试验数据

2、楔形模型试验数据如下表3。

Table 3. Wedge model test data

表3. 楔形模型试验数据

3、锥形模型试验数据如下表4

Table 4. Cone model test data

表4. 锥形模型试验数据

4、梯形模型试验数据如下表5

Table 5. Trapezoidal model test data

表5. 梯形模型试验数据

用立体角表征模型结构，通过MINITAB软件分析试验数据，判断模型厚度与其立体角之间是否存在必然联系。

显然，对于长方形模型，楔形模型，锥形模型以及梯形模型，其膜厚与立体角存在一定的线性关系。

结论1：铝层膜厚与模型可接受镀铝的立体角Ω成正比关系：

膜厚 = K × 立体角a

结论2：不同侧面及不同结构的区别表现在系数K、a的差异上。

4.2. 确定系数K、α

考虑蒸发源与镀铝面的相对位置对膜厚均匀性也存在影响 [4]，引入相对蒸发源角度的概念(如下图7)，这里是指从电极上的蒸发源出发，作垂直于电极的垂线，与镀铝面相交的角度θ。

运用数据分析软件等技术手段，分析蒸发源角度的不同对于膜厚和立体角的关系 $d=f\left(\Omega \right)$ 的影响，结果如下图8：

显然得到结论：相对蒸发源角度θ越大，膜厚越厚。

为确定表达式(2)中待定系数K和Ω，以便给出膜厚与立体角的关系式，在试验过程中考虑蒸发源角度的影响。

Figure 7. Angle of evaporation

图7. 蒸发源角度

Figure 8. The curve of solid angle

图8. 立体角曲线

为了减少误差，实验时保持相关实验条件的一致性，选用相同的镀铝机以及相同的镀铝技术参数，这里铝量选用14圈(7圈 × 2)，结果如下表6。

Table 6. Test data considering angles of evaporation

表6. 考虑蒸发源角度的试验数据

通过MINITAB对上述试验数据进行分析，易得出系数K与cosθ的关系式：

$K=66.63-29.38\cos \theta +3.47{\cos }^2\theta -18.28{\cos }^3\theta$ (3)

系数α与cosθ的关系式：

$\alpha =32.69-24.37\cos \theta +97.83{\cos }^2\theta -91.26{\cos }^3\theta$ (4)

注1 实际工作中，确定了蒸发源与镀铝面的相对位置，即确定了θ角，利用(3)和(4)，可计算出K和α，再带入公式(2)中，得到膜厚与立体角的关系。

注2 公式(1)是对不同的结构的零件模型化：首先通过CATIA软件测出每个面的平面角，然后带入到公式(1)计算立体角；公式(2)是对不同的结构的零件设计符合均匀性要求的膜层厚度。

5. 实例分析

以EBO A SH后组合灯2壳体(右边)为例，验证白色区域点A1、A2的铝层设计的膜厚是否符合要求，如下图9。

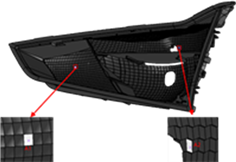
Figure 9. The housing of EBO A SH

图9. EBO A SH后组合灯2壳体

首先用我司现有的测厚仪对EBO A SH 后组合灯2壳体的白色区域点A1、A2的铝层膜厚进行实际测量，获得A1点的铝层膜厚为14.7 mm，获得A2点的铝层膜厚为10.43 mm。现在使用本文计算膜厚的方法，判断实际膜厚是否是合理的设计。

先将零件开口现状线段化，把零件边界线条中所有弧线段，取中点，分别与弧线段两端相连。再将多边形使用线段分割成三角形，如下图10所示：

Figure 10. Polygon segmentation

图10. 多边形分割

将多边形使用线段分割成三角形，如上图中蓝色线段所围成的图形所示。每个三角形与A1点构成多面体，以A1点为顶点，每个多面体的立体角为 ${\Omega }_1$ 、 ${\Omega }_2$ 、 ${\Omega }_3$ 、 ${\Omega }_4$，如下图11。

Figure 11. Calculate solid angle

图11. 计算立体角

对于 ${\Omega }_1$ 的计算，将模型导入CATIA中，可测得α，β，γ角，将α、β，γ代入公式(1)，可计算出立体角 ${\Omega }_1$ 的度数，如下图12：

Figure 12. Degree of ${\Omega }_1$

图12. ${\Omega }_1$ 的度数

同理可分别计算出 ${\Omega }_2$ 、 ${\Omega }_3$ 、 ${\Omega }_4$ 的大小，从而得到A1点对于的立体角： $\Omega ={\Omega }_1+{\Omega }_2+{\Omega }_3+{\Omega }_4=1.18$。类似的步骤可计算出A2点对应的立体角 $\Omega =1.07$。

计算膜厚，需要先测量蒸发源角度θ，见图13：

Figure 13. Measure the degree of θ

图13. 测量蒸发源角度θ

过A点沿拔模方向作一条直线c1，沿A点所在的平面作与零件开口所在平面平行的直线c2。易测得c1、c2间的夹角θ为5.571，带入到K，α表达式中：

$K=66.63-29.38\cos \left(5.571\right)+3.47{\cos }^2\left(5.571\right)-18.28{\cos }^3\left(5.571\right)$

$\alpha =32.69-24.37\cos \left(5.571\right)+97.83{\cos }^2\left(5.571\right)-91.26{\cos }^3\left(5.571\right)$

于是有 $K=38.452$， $\alpha =30.717$，将K值和α值带入膜厚的计算公式(2)中，得到具体膜厚与结构的表达式：

$膜厚=38.452\times \Omega -30.717$ (5)

将A1点计算出来的立体角 $\Omega =1.18$ 代入(5)式得：

$\text{A}1点铝层膜厚=38.452\times 1.18-30.717\approx 14.656$

将A2点计算出来的立体角 $\Omega =1.07$ 代入(5)式得：

$\text{A}2点铝层膜厚=38.452\times 1.07-30.717\approx 10.427$

与目前实际的膜厚(A1点实际铝层膜厚14.7 mm，A2实际铝层膜厚10.43 mm)对比，基本符合设计要求，效果较佳。

6. 结论

本文考虑了汽车车灯在镀铝工艺方面，零件结构的复杂性对镀铝层膜厚均匀性的影响，研究了镀铝件结构与镀层膜厚的关系。通过引入立体角的概念，刻画不同的立体几何模型，对四种不同结构的模型，论证了铝层厚度与零件结构的关系是呈线性的。本文给出了开口平面为多边形的几何体，镀层厚度的设计方法。最后数值仿真说明了本文结论的有效性。

参考文献