1. 引言
滑坡是地质灾害的主要类型之一,为减少滑坡地质灾害给人民生命财产和国民经济建设带来的威胁,对滑坡稳定性进行预测分析十分必要。目前,滑坡稳定性分析常使用有极限平衡法和数值分析法 [1] [2]。其中极限平衡法主要有Fellenius法、Bishop法、Janbu法、Spencer法、Morgenstern-Price法、Sarma法和不平衡推力传递法。常用的数值分析法主要有离散元法、有限元法和有限差分法等。刚体极限平衡条分法力学模型简单,已经被广泛地应用于工程实践中,并积累了丰富的实践经验,在计算中,只需要少量的岩土力学参数,计算结果可以直接作为工程设计应用的稳定性指标 [3]。陈羽等 [4] 运用不平衡推力传递系数法和瑞典条分法确定某隧道洞口滑坡安全系数,对滑坡稳定性进行了评价。饶平平等 [5] 将拟动力法和简化毕肖普法结合,以用来研究坡顶抗滑桩加固土质边坡在地震力作用下的动态稳定性。王世梅 [6] 以涉水边坡为研究对象,运用有限元法,探讨了不同库水位升降速率对于滑坡渗流场和稳定性的影响,张永昌等 [7] 应用有限元强度折减法,对库水位在不同速率变动情况下树坪古滑坡的复活机理开展了研究。在对边坡稳定性进行评价时,闰云明 [8] 考虑弹性模量和泊松比的影响,采用改进的有限元强度折减法进行评价。
但针对滑坡体稳定性分别采用极限平衡法以及强度折减法等方法系统研究还并不多见。为此,本文以某滑坡体为例,在分析其地质条件以及滑坡特征基础上,首先使用理正软件运用简化Janbu法求得滑坡体的滑动安全系数,然后采用FLAC3D软件建立该滑坡体的模型,并运用强度折减法计算出已建立模型的滑坡体的安全系数,最后对两种方法的计算结果进行分析,此研究成果可为工程实践提供指导。
2. 工程地质条件
2.1. 地形地貌
勘查区位于低丘坡脚地带,地形呈东北高西南低的圈椅形,其北部、东部及西部均有微分水岭,第一斜坡带与坡脚相对高差在60米左右,山坡20˚~30˚之间,斜坡体上植被发育。勘查区地貌属大别山中低山区,地形起伏变化较大,最高点位于勘查区北2 km的鹰嘴岩,标高528 m,最低点50 m (长河边),地形相对高差478 m。微地貌为低山山坡及冲沟。勘查区所在山坡上陡下缓,勘查区以北地形坡度多在25˚以上,勘查区内地形坡度在25˚左右,屋后切坡80˚,岩性由太古界刘畈组片麻岩地层组成,山坡植被茂密,成因类型为侵蚀剥蚀。山坡冲沟发育,宽度变化大。
2.2. 滑坡物质组成
根据区域地质资料和勘查资料,将勘查区工程地质体划分为岩体和土体两大类。
1) 较坚硬~坚硬变质岩岩组:
岩性为太古界刘畈组二长片麻岩、浅粒岩。鳞片状、粒状变晶结构,片麻状构造,新鲜岩石饱和抗压强度在80~100 MPa,软化系数小于0.68。浅部岩石风化强烈,全–强风化带厚度变化大,一般2~5 m,滑坡体上钻孔中揭露的全–强风化带厚度1.0~8.0 m,断层破碎带强风化带厚度 > 10 m,风化后的岩石松软,呈砂土、砂砾状、镐锄易挖。
2) 土体
全新统残坡积层,主要为砂质粘性土,局部为碎石土。
褐黄色,可塑,主要成分粉质粘土,含少量碎石角砾,厚度0~3.10 m。局部碎石含量大于70%,为褐黄色含碎石粉质粘土。承载力特征值fak = 120 KPa。
据取样测试,如表1所示,其物理力学性质指标如下:

Table 1. Sampling test physical and mechanical indicators
表1. 取样测试物理力学指标
3. 滑坡稳定性对比分析
3.1. 极限平衡法计算安全系数
极限平衡方法,是将有滑动趋势范围内的边坡土体沿某一滑动面切成若干竖条或斜条,在分析条块受力的基础上建立整个滑动土体的力或力矩平衡方程,并以此为基础确定边坡的稳定安全系数。在极限平衡方法理论体系的形成过程中,出现过一系列简化的方法,常见的有瑞典法、Bishop法、Janbu法、Sarma法等。这些方法均假设土体沿着一个潜在的滑动面发生刚性滑动或转动,滑动土体是理想的刚塑性体,完全不考虑土的应力–应变关系,并认为沿滑动面上各点的强度发挥程度及抗剪强度折减安全系数相同,其安全系数的表述与滑坡体所在区域的变形特点和滑坡体外区域的地质情况、受力条件等完全不发生关系。各方法不同的地方仅在于为消除超静定性而对条间力或滑动面上相互作用力所做的假设以及推求安全系数所用的方法各不相同而已。由于各种极限平衡方法具有模型简单、公式简捷、便于理解等优点,因此在一些仅需简单分析的工程中得到了较为广泛的应用 [9]。
简化Janbu法是针对实际工程中碰到的非圆弧滑动面的问题而提出的一种极限平衡方法,其假设有:① 滑动面上的切向力Ti即是滑动面上土所发挥的抗剪强度;② 土条两侧法向力E的作用点位置为已知,且一般假定作用于土条地面以1/3高度处。如图1所示为Janbu法受力示意图:

Figure 1. Schematic diagram of Janbu general rule of force
图1. Janbu普遍条分法受力示意图
1) 计算剖面的确定
根据滑坡的实际情况及应急勘查工作的剖面布置情况,取主勘探剖面线作为滑坡稳定性计算的剖面。
2) 计算参数的确定
根据取样室内试验及反演计算并参考地区经验数据综合确定各岩土体取值,如表2所示。

Table 2. Value of each rock and soil body
表2. 各岩土体取值
3) 稳定性分析计算结果
根据该滑坡体的岩土体物理参数,在理正6.5软件中建立斜坡模型,并通过软件采用简化Janbu法对边坡进行安全系数计算分析。在计算过程中,只考虑斜坡体自重,不考虑地震影响,模型的计算简图和计算结果图如图2和图3所示。

Figure 3. Janbu calculation result graph
图3. Janbu计算结果图
由图3可知,该滑坡体的安全系数为0.846,处于不稳定状态。
3.2. FLAC3D强度折减法验算安全系数
与极限平衡法相比,强度折减系数法不需要任何假定,便可自动求得任意形状的临界滑移面及其对应的最小安全系数,同时它还可以真实反映坡体失稳及塑性区的开展过程 [10]。
3.2.1. 强度折减法的基本原理
强度折减法通常适用于安全系数的计算,它是通过逐步减小材料的强度使边坡达到极限平衡状态来实现的 [11]。对于Mohr-Coulomb破坏准则来说,安全系数F根据公式(1)和(2)来定义 [12]。
(1)
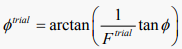 (2)
(2)
式中:
为折减后的黏聚力;
为折减后的内摩擦角;
为折减系数。
3.2.2. 边坡失稳判断依据
有限元强度折减法的原理简单,但难以判断边坡是否达到临界破坏状态。在对边坡进行稳定性分析时,判断边坡失稳破坏的标准有:位移突变准则、塑性区的贯通准则、收敛性准则、广义剪应变准则或广义塑性应变准则、动力学判据 [13]。
1) 位移突变准则。利用计算得到的域内某一部位的位移与折减系数之间关系的变化特征确定失稳状态,当折减系数增大到某一特定值时,某一部位的位移突然增大,则认为边坡发生失稳 [14]。
2) 塑性区的贯通准则。土体处于塑性状态后,其位移无限增大。当整个边坡中塑性区连贯时,认为边坡已经产生滑动破坏 [15]。
3) 收敛性准则。通过有限元数值计算是否收敛来判断边坡是否稳定。若计算收敛,则认为边坡稳定;若计算到某一数值时,计算结果刚好不收敛,则认为边坡破坏,此时的折减系数即为安全系数 [16]。
4) 广义剪应变准则或广义塑性应变准则。该准则认为某一幅值的等值线从坡底贯通到坡顶时,意味着边坡达到极限状态 [17]。
5) 动力学判据。运用动力学的思想来分析强度折减过程中边坡的特征,以加速度是否为零作为边坡是否稳定的判据 [18]。
3.2.3. 模型建立及参数的选取
在建立滑坡几何模型时,滑坡地表形态及内部岩层分布特性等均是严格遵照地质勘测相关图集资料;坡体形态及相关建筑物的空间分布形态的关键点直接从相关设计图中读取,然后再进行相应的模型构建,模型主要分为三部分:滑坡体、滑坡带以及滑床三组,如图4所示。
3.2.4. 数值计算结果及分析
通过建立的滑坡模型图,运用强度折减法后计算得到了该滑坡体的位移矢量图,如图5,以及滑坡体剪切应变增量图,如图6。

Figure 5. Sliding body displacement vector
图5. 滑体位移矢量图
由图5可知,坡体后缘位移较小,但坡体前缘存在着较大的位移量,而且越接近坡脚位移量就越大,原因可能为滑床表面受到滑坡体滑动的牵引,造成前缘产生了一定的下滑量。由图6可知,滑床及滑坡体后缘保持稳定,未发生变形破坏。滑坡体前缘的滑带处剪应变增量较大,剪应变集中带已经贯通,剪切带已经形成,滑动带已明显贯通。
通过计算得出该滑坡体安全系数为0.908,该滑坡体具有一定的危险性。与理正岩土计算结果相比略大,原因可能为此模型简化了一些较小的斜坡面。依据《滑坡防治工程勘查规范(GBT32864-2016)》对其稳定性进行评价,与Janbu法计算分析得出的结论是一致的:该滑坡体具有一定的危险性,属于不稳定滑坡,需要对其采取措施,以防止滑坡灾害的发生。
4. 结论
采用极限平衡法中简化Janbu法,求出滑坡体安全系数为0.846,然后再对滑坡体稳定性进行分析;再采用强度折减法,求出其安全系数为0.908,然后再分析滑坡体的稳定性。依据《滑坡防治工程勘查规范(GBT32864-2016)》对滑坡体稳定性进行评价,结果表明:与简化Janbu法得出的安全系数相比,采用强度折减法得出的安全系数的数值较高,安全系数存在差异的原因可能是由于两种方法都受到人为因素和计算模型建立简略的影响,但依据规范,最终得出的结论一致,该滑坡体处于不稳定状态。