1. 绪论
幂级数是函数项级数的一种特殊情形,也是数学分析中非常重要的内容,不论在数学方面还是其他学科中都有广泛的应用。幂级数在收敛区间绝对收敛,并且具有逐项积分、逐项求导等性质。巧妙利用幂级数的展开式以及性质把一些较为复杂的问题转化为简单形式,在解题时往往思路清晰,条理清楚。幂级数和函数在不定积分、导数、数列极限、不等式等相关数学分支中应用广泛,因此研究幂级数收敛域、和函数是非常重要的。本文可分为以下四个部分:1) 绪论:主要介绍了为何选取此课题。2) 预备知识:分别介绍了幂级数,幂级数收敛,幂级数和函数的基本理论知识。3) 主要结论:对幂级数收敛,幂级数和函数的理论知识进行深层次挖掘。对于幂级数收敛域的问题,分为具体型与抽象型两种;在求和函数的问题中,总结归纳和函数的求解思路,利用四则运算,逐项求导,逐项积分求取和函数。4) 结论:主要对本文内容进行总结概括,以及在学习幂级数的心得体会。
2. 预备知识
2.1. 幂级数的概念
1) 函数项级数:设函数列
定义在区间I上,称
为定义在区间I上的函数项级数,记为
,当x取确定的
时,
成为常数项级数
。
2) 幂级数:若
的一般项
是n次幂级数,则称
为幂级数,它是一种函数项级数,其一般形式为
,其标准形式为
,其中
为幂级数的系数。
3) 收敛点与发散点:若
,有
收敛,则称点
为幂级数
的收敛点;若给定
,
发散,则称点
为幂级数
的发散点。
4) 收敛半径:对任意给定的幂级数,必存在唯一的r (r满足
),使得幂级数在
绝对收敛,在
发散,r为收敛半径。
5) 收敛域:函数项级数
的所有收敛点的集合称为它的收敛域。
6) 和函数:在收敛域上,记
,并称
为
的和函数。
2.2. 幂级数的收敛
1) 阿贝尔第一定理:当幂级数
在点
处收敛时,对于满足
的一切x,幂级数绝对收敛;当幂级数
在点
处发散时,对于满足
的一切x,幂级数发散 [1]。
2) 收敛半径r求法:若幂级数
的相邻两项系数之比满足条件
则幂级数的收敛半径
(
时理解为
时理解为
)。
证明:用达朗贝尔判别法,
,
,则当
时级数绝对收敛,则当
时级数发散。若
,则级数对任意当x绝对收敛。当
时,级数在
外发散,证毕 [1]。
3) 收敛区间与收敛域的求法:a) 求收敛半径r;b) 开区间
为幂级数
的收敛区间;单独考察幂级数在
处的敛散性就可以确定其收敛域为
或
或
或
。
2.3. 幂级数的和函数
1) 运算法则
若幂级数
与
的收敛半径分别为
和
则有:
a)
,
,k为常数;
b)
,
。
2) 和函数的性质
a) 幂级数
的和函数
在其收敛区间I上连续,且如果幂级数在收敛区间的端点
(或
)处收敛,则和函数
在
或
上连续 [2]。
b) 幂级数
的和函数
在其收敛域I上可积,且有逐项积分公式
,逐项积分后所得到的幂级数与原级数有相同的收敛半径,但收敛域可能扩大。
c) 幂级数
的和函数
在收敛区间
内可导,有逐项求导公式
,逐项求导后所得到的幂级数与原级数有相同的收敛半径,但收敛域可能缩小。
3. 主要结论
3.1. 幂级数的收敛域
为了具体说明考研数学中对于幂级数收敛域的考察情况,本文总结了关于收敛域的两种出题角度,第一种给出的研究对象是具体的,第二种给出的研究对象是抽象的。
3.1.1. 收敛域的具体型问题
1) 对于
a) 求收敛半径,若
,则幂级数
的收敛半径 [3]:
(3.1)
b) 开区间
为幂级数
的收敛区间;单独考察端点处的敛散性,确定收敛域。
例1 求幂级数
的收敛域。
解令
,则
,在
时,幂级数
发散,当
时,幂级数
是一个交错级数,由莱布尼茨判别法可知级数条件收敛,故收敛域为
。
2) 通过换元法将幂级数
改为标准幂级数
[3]。
例2 求级数
的收敛域。
解令
,得级数
其收敛半径
(3.2)
当
时,级数成为
,这是交错级数,设
,由于
,达朗贝尔判别法失效,但是,因为
,即数列
严格单调递增,而
,所以当
时,
一般项不趋于0,级数发散。当
时,级数显然也发散。故级数
的收敛域为
,从而原级数的收敛域为
。
3) 对于缺项幂级数
a) 加绝对值,即写成
,
b) 用正项级数的达朗贝尔(或者柯西)判别法。
(或
)<1,求出收敛区间
。
c) 单独讨论收敛区间两个端点的敛散性,从而确定收敛域。
例3求幂级数
的收敛域。
解
,由于
,故当
时,
收敛;当
时,
,根据莱布尼茨判别法知此级数收敛。故幂级数
收敛域为
。
3.1.2. 收敛域的抽象型问题
考研对于求解收敛域的抽象问题大概有2种 [2]。
1) 根据阿贝尔第一定理,已知
在点
的敛散性,则该幂级数的收敛半径可以分为3种。
a) 如果幂级数在
处收敛,则收敛半径
,
b) 如果幂级数在
处发散,则收敛半径
,
c) 如果幂级数在
处条件收敛,则收敛半径
。
2) 已知
的敛散性信息,求
的敛散性
a)
与
的转化一般通过平移收敛区间、提出或者乘以因式
;
b)
与
的转化一般通过对级数逐项求导、逐项积分得到;
c) 以上对幂级数的变形(平移收敛区间、提出或者乘以因式
、对级数逐项求导、逐项积分)都不改变收敛半径,但幂级数收敛域可能变化 [4]。
例 4 证明
在点
处条件收敛,则幂级数
在点
处绝对收敛。
解由
在点
处条件收敛,根据阿贝尔第一定理
,且收敛区间为
;将
转化为
,即把级数的中心点−1转移到1,故收敛区间平移到
,得到
收敛半径不变;对
逐项求导,得
,再逐项乘以
得
,收敛半径不变,收敛区间不变。故
的收敛区间为
,
在收敛区间内部,故该点处级数绝对收敛,得证。
3.2. 求和函数
求解幂级数和函数时需要先求出收敛半径,进而求得收敛域,然后再求幂级数收敛域上的和函数。通常在求和函数的过程中我们依赖四则运算法则,恒等变形以及一些基本级数的和函数形式。
3.2.1. 和函数的运算
1) 恒等变形
a) 通项、下标一起变,其中l为整数,可正可负可为0,如
;
b) 只变下标,不变通项,如
;
c) 只变通项,不变下标
。
2) 一些基本级数的和函数
a)
;
b)
;
c)
;
d)
;
e)
;
f)
。
3.2.2. 幂级数求和函数
1) 直接套公式(利用已知的基本级数的和函数)
例5 求幂级数
的和函数。
解因为
,
,所以
。故
。
2) 先导后积或先积后导求和函数(一定在收敛区间求)
a) 当
在分母上时,先导后积
注:在题目中验证
是否等于
,事实上由于
故
;又由于当a为中心点时,
都收敛,故下限a通常取中心点。
例 6求级数
的和函数。
解设
,逐项求导,得
,
,然后两边积分,得
,又因为
,故和函数
,
(3.3)
b) 当
在分子上时,先积后导
例 7求级数
的和函数。
解
,设
,则原级数
。对
两边积分,得
,
。再两边求导,得
(3.4)
所以
,
。
3) 运用四则运算法则
例 8求幂级数 的和函数
的和函数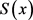 。
。
解先利用幂级数的运算法则,如加减法:得到幂级数 然后利用已有的几个初等函数的幂级数展示求和,得:
然后利用已有的几个初等函数的幂级数展示求和,得:
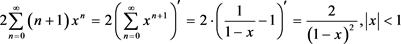 (3.5)
(3.5)
 (3.6)
(3.6)
故原级数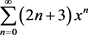 等于
等于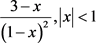 。
。
3.2.3. 和函数的应用
1) 计算积分 [5]
例 9计算不定积分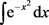 。
。
解根据公式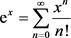 ,则
,则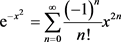 ,从而
,从而
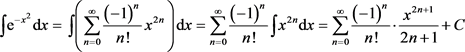 (3.6)
(3.6)
2) 计算导数
例 10设 由方程组
由方程组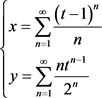 所确定,求
所确定,求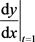 。
。
解 ,分别对
,分别对 求导,
求导,
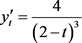 ,
,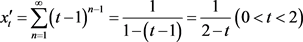 (3.7)
(3.7)
则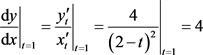 。
。
注: 易于求和函数,故求和后再求导;
易于求和函数,故求和后再求导;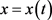 不易于求和函数,故求导后再求和。
不易于求和函数,故求导后再求和。
3) 求数列极限
例 11求极限 。
。
解由于 为正项级数,设
为正项级数,设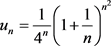 ,由
,由
 (3.8)
(3.8)
知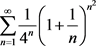 收敛,因此
收敛,因此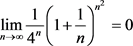
4) 证明不等式
例 12证明不等式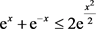 ,
,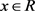 。
。
证明因为 ,
,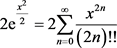 ,而
,而 故原不等式成立。
故原不等式成立。
注: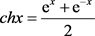 是双曲余弦函数,它的图像在数学中称为悬链线。
是双曲余弦函数,它的图像在数学中称为悬链线。
4. 结论
本文主要讨论了幂级数收敛与和函数在数学分析以及考研数学中的解题方法。
论文首先给出了幂级数收敛以及和函数的相关理论知识。然后,对幂级数收敛与和函数在考研数学中的应用进行了总结归纳。其中,在求幂级数收敛域的问题中,由于求收敛域和收敛半径题目类型多样,为更好更快地解决问题,需要分“具体型”和“抽象型”两种类型求解,在上述过程中我们通过例题总结出一般的解题规律。在求和函数的问题中,本文对不同情况下和函数的求解思路进行总结,利用四则运算,逐项求导,逐项积分求取和函数,在计算过程中灵活变形,具体问题具体分析,使得问题得到很好的解决;紧接着本文描述了幂级数和函数在不定积分,导数,数列极限,不等式等相关数学分支中的应用。
为了更好学习幂级数这一节内容,我系统总结了几种求收敛域、和函数的方法。通过总结收敛域求法有两种类型,具体型和抽象型。其中具体型主要是根据达朗贝尔判别法得到收敛半径,然后根据数项级数的收敛性判别方法判断端点处的收敛性,求得收敛域;抽象型根据阿贝尔第一定理,以及对原级数平移,求导,积分(不改变收敛半径)得到所要求级数的收敛域。和函数主要学到了如何求和函数值以及利用幂级数和函数求解其他数学问题,如求极限、求导、求不等式以及求积分等等。利用逐项积分,逐项求导,四则运算法则拆分等方法求取和函数的值时一定要注意和函数成立的条件是在收敛域内,这一点尤为重要。