1. 引言
链传动是常用的传动方式之一,通过链轮与链条的啮合传递动力,具有负载能力大、无弹性滑动、传动效率高和平均传动比准确等优点 [1]。Saito等、Noguch等和王慧等 [2] [3] [4] 分析了滚子链的失效形式,当链轮与链条啮合时,其摩擦形式为滑动摩擦,此时滚子与套筒易发生疲劳破坏。不同型号的链条尺寸不同,随着销轴、套筒直径的增大,两者形成的销轴–套筒有限长线接触副的接触区也会变大,对接触区内的润滑状态会产生很大影响。
Liu [5] 等通过理论分析研究了轴承滚子等效曲率半径R对滚子副润滑状态的影响。Zhang [6] 等采用数值分析的方法,研究了链条套筒和销轴的等效曲率半径R对接触区内的油膜厚度、压力、温升和摩擦系数的影响。刘晓玲和杜肖 [7] 通过光干涉实验研究滚子副润滑状态的转变,当载荷减小或者卷吸速度增加,滚子副润滑状态逐渐由弹流润滑转变为流体动力润滑。钟伟杰等、吴继强等和华同曙等 [8] [9] [10] 从实验和理论研究了滚子的边缘效应,为滚子轮廓优化设计提供了依据。
关于滚子副润滑情况的文献,大多是针对滚动轴承的研究 [7] [8] [9] [10],运动形式也以滚动居多。基于链传动的滑动条件下滚子副润滑情况的研究,尚不多见。本研究使用光干涉测量方法,使用滚子–盘有限长线接触副,模拟链传动中销轴与套筒或滚子的接触,运动形式为纯滑。通过改变滚子的尺寸、载荷和滑动速度等参数,研究滚子尺寸对润滑油膜厚度及润滑状态的影响。
2. 实验设置
2.1. 实验装置
本实验采用光干涉法测量油膜形状及厚度,在实验室自主研发的光弹流试验台上进行。采用双色光干涉强度调制技术 [11],光干涉图像对比度高,膜厚分辨率为1 nm,可高效准确的测量4 μm范围内的润滑油膜厚度。实验装置示意图如图1所示,实验台由载荷加载系统、运动控制系统和图像采集系统等组成。
加载装置由手摇螺杆、载物平台和压力传感器组成。运动控制系统主要由工控机、伺服电机、伺服放大器和减速器组成。图像采集系统主要由光源、显微镜、CCD相机、图像采集卡、计算机等五部分组成。本实验采用的是红绿双色RG激光光源(红光波长λ = 635 nm,绿光波长λ = 532 nm)。CCD相机负责采集经过显微镜放大的光干涉图像,采集到的信号为模拟信号,每秒钟可采集光干涉图像120张。图像采集卡负责AD转换及缓存图像。计算机通过软件控制光干涉图像的采集和存储。
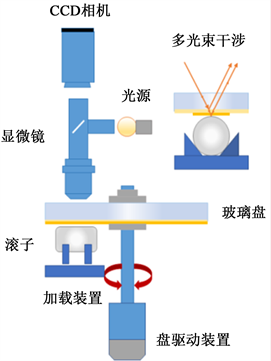
Figure 1. The schematic diagram of testing
图1. 试验台示意图
2.2. 实验条件和材料
实验过程中控制环境温度为24℃ ± 0.5℃,湿度为60% ± 5%。玻璃盘做恒速旋转运动,滚子固定不动,运动状态为纯滑。供油条件为充分供油。
玻璃盘为K9玻璃盘,弹性模量为81 GPa,泊松比为0.208。玻璃盘上镀有公称厚度15 nm的析光Cr膜和公称厚度为120 nm的SiO2垫层,镀层的表面粗糙度Ra = 4 nm。滚子材料为GCr15,弹性模量为208 GPa,泊松比为0.3。为得到更好的光干涉图像,滚子表面做抛光处理。实验所用滚子长度为24 mm,滚子直径分别为12 mm、18 mm和24 mm。试验用润滑油为CK润滑油,40℃时动力粘度为89.34 mPa∙s,100℃时动力粘度为12.44 mPa∙s,密度为668 kg/m3。
3. 数学模型及数值方法
为了验证本文的实验结果,我们使用弹流润滑理论,建立了一个有限长线接触弹流润滑模型,如图2所示。图中,a为滚子,b为玻璃盘,r为滚子的半径,l0为滚子的母线长度,ysk为滚子圆角区域的长度,rend为修形圆角半径。
计算过程中使用的方程如下:
Reynolds方程 [12] 为
(1)
油膜厚度方程 [12] 为
(2)
其中hend的表达式为
(3)
润滑油膜的能量方程 [12] 为
(4)
两固体能量方程(即热传导方程) [12] 为
(5)
润滑油的粘温粘压关系 [12] 为
(6)
润滑油的密压密温关系 [12] 为
(7)
载荷平衡方程 [12] 为
(8)
Reynolds方程的边界条件为
(9)
油膜上游温度的边界条件为
(10)
固体的能量方程的边界条件 [12] 为
(11)
油膜压力采用多重网格法 [12] 计算,弹性变形项用多重网格积分法 [12] 求解。本文全部计算均在无量纲后进行,使用4层网格,在最稠密的网格层上,X方向上的节点数为128,Y方向上的节点数为10。温度计算采用逐列扫描法 [12]。收敛精度方面,压力的相对误差小于10−3,温度的相对误差小于10−4,载荷的相对误差小于10−4 。计算中使用与实验中相同的载荷和卷吸速度以及润滑油黏度参数,计算后使用Origin软件绘制膜厚图。
4. 结果与讨论
在钢制滚子与K9玻璃盘组成的有限长线接触运动副中,通过改变玻璃盘的转速,获得不同的滑动速度(0.02 m/s、0.1 m/s、0.2 m/s、0.3 m/s和0.4 m/s)。最大赫兹接触压力设置为50 MPa和100 MPa两种。
4.1. 滚子尺寸对接触区内润滑油膜厚度的影响
图3给出了在最大赫兹接触压力分别为50 MPa和100 MPa条件下,随滑动速度的增加,3种滚子的中部与玻璃盘之间所形成的最小膜厚变化情况,最小膜厚均随着滑动速度的增加而增加。2种载荷条件下,最小膜厚都随着滚子直径的增加而增加。当其它参数相同的条件下,载荷越轻,最小膜厚越厚。
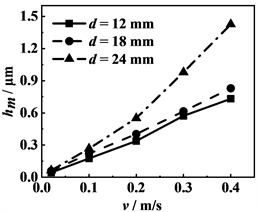 (a) PH = 50 MPa
(a) PH = 50 MPa 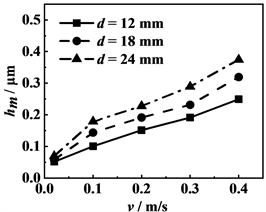 (b) PH = 100 MPa
(b) PH = 100 MPa
Figure 3. The polyline diagram of the minimum film thickness in the middle region of the roller under different sliding speeds
图3. 不同滑动速度条件下滚子中部区域最低膜厚曲线图
图4给出了PH = 100 MPa,v = 0.3 m/s条件下3种滚子直径中部的中截面膜厚曲线对比图和光干涉图像,入口在接触区右侧,速度方向如箭头所示。从膜厚曲线对比图可见,油膜厚度随滚子直径的增加而增厚。光干涉图中可见在滚子轴向,因为滚子的圆柱度不够,图像出现不均匀现象。事实上,作者已尽力打磨了滚子,可以想象在实际销轴–套筒形成的有限长线接触中,由于制造加工误差的存在,销轴的圆柱度也一定存在更严重的问题,对接触和承载造成一定的影响。
图5给出了与图4对应的理论分析结果,即在PH = 100 MPa,v = 0.3 m/s条件下3种滚子直径的中截面膜厚曲线对比图和膜厚等值线图,入口在左侧。理论分析结果的趋势与实验结果一致,油膜厚度随滚子直径的增大而增加。滚子直径增大,中部膜厚增大。作者认为滚子直径增大,加剧了端部的应力集中现象,端部压力值增大,中心压力减小,从而导致接触区中心膜厚增加。由于实验条件限制,本文并没有得到滚子端部区域的实验结果。与实验结果不同的是,滚子中截面最低膜厚出现在接触区中心,且膜厚低于实验膜厚。在PH = 100 MPa的轻载荷条件下,接触区温升很小,可以忽略。故本文没有给出油膜中温升曲线图。
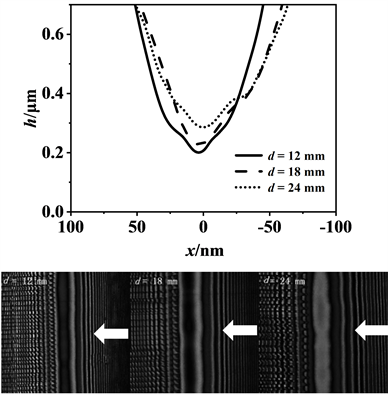
Figure 4. Film thickness curve and optical interferometric image of different radius roller under middle region (PH = 100 MPa, v = 0.3 m/s)
图4. 不同直径滚子中部径向膜厚曲线图和光干涉图(PH = 100 MPa, v = 0.3 m/s)
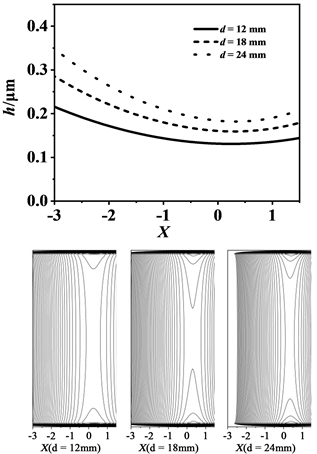
Figure 5. Radial film thickness curves and film thickness contour diagram of different radius rollers (PH = 100 MPa, v = 0.3 m/s)
图5. 不同直径滚子中部径向膜厚曲线和膜厚等值线图(PH = 100 MPa, v = 0.3 m/s)
4.2. 滑动速度对接触区内润滑油膜厚度的影响
图6给出了滚子直径为12 mm,最大赫兹应力为100 MPa条件下,随玻璃盘滑动速度的增加,接触区中部油膜光干涉图和中截面曲线图的变化。入口在接触区右侧,速度方向如箭头所示。由光干涉图的变化可见,在滑动速度较低的条件下,接触区较宽,对应的油膜厚度只有0.1 μm左右。随着滑动速度的增加,形状逐渐变为楔形,油膜厚度逐步增加。
5. 结论
1) 实验结果表明,接触区中截面油膜厚度随滚子直径的增加而增加。
2) 理论分析结果的趋势与实验结果一致,油膜厚度也随滚子直径的增加而增加。有些不同的是计算所得膜厚略低于实验测得膜厚。
3) 在滑动速度较低时,接触区较宽,随滑动速度增加,油膜形状逐渐变为楔形,油膜厚度逐步增加。
基金项目
国家自然科学基金(51875298);山东省自然基金(ZR2019MEE040)。
NOTES
*通讯作者。