1. 引言
光子晶体是折射率或介电常数周期性变化的人工微结构材料,其概念最早于1987年分别由 S.John和E.Yablonovitch提出 [1] [2],光子禁带和光子局域是光子晶体的基本特性。早些年的研究主要集中在常规光子晶体上,常规光子晶体的带隙位置和带隙宽度不容易按需求设计。随着光子晶体的应用范围日益广泛,对光子晶体的带隙中心位置和带隙宽度有更多的要求,需要能够按照要求调控光子晶体的带隙,近年陆陆续续提出了不同结构的非常规光子晶体 [3] - [8],折射率与空间坐标有关的函数型光子晶体 [9] [10] 就是其中的一类非常规光子晶体。函数型光子晶体利用材料的非光学性质,即折射率与电场的非线性关系:
,通过电场强度改变介质的折射率,进而调控光子晶体的带隙。一维函数型光子晶体得到了比较深入的研究,主要原因是使用转移矩阵方法,对带隙的计算比较方便。二维函数型光子晶体的研究,目前文献都集中在折射率随半径变化的函数关系上 [11] [12],也就是电场强度在介质柱的半径方向上发生变化,进而改变介质柱的折射率在半径方向的分布。但是,在实验中控制每个介质柱中的电场在半径方向发生改变,难度很大。笔者发现,在实际制造光子晶体过程中,更容易实现的是,在二维平面内,让折射率均匀分布的介质柱周期排列,介质柱在指定方向折射率阶梯增加。通过介质柱半径和晶格常数的调节,来人为控制二维光子晶体的带隙位置和带隙宽度。本文通过模拟二维折射率阶梯增加的光子晶体的带隙,结果表明,通过调节二维光子晶体的圆柱半径和晶格常数,可以人为调节光子晶体的带隙位置和带隙宽度。这为光子晶体的设计提供新的思路和理论依据。
2. 折射率阶梯增加的二维光子晶体结构
在光子晶体的模拟计算中,使用较多的方法为:平面波展开方法,有限时域差分方法(FDTD),转移矩阵方法。平面波展开法应用比较广范,可以计算在第一布里渊区间,能带与波矢的关系,但是,该方法对晶体的完整性要求比较高,难以适用于非周期性结构和不规则的边界;转移矩阵方法适用于一维,且具有周期性结构的光子晶体。有限时域差分方法(FDTD)以Maxwell方程为基础,通过离散方法,计算电磁波在光子晶体内的传播,可以适用于非周期性的结构,和不规则的边界,适应面很广。
FDTD方法,是由K.S.Yee在1966年提出的 [13],其基本思想是把数学中的微分用差分代替,用中心差分法表达导数为 [13]:
由于计算机的储存容量的限制,计算的物理区间是有限的,用FDTD方法计算时,被广泛使用的是
完全匹配吸收层 [14] (PML),通过选择边界内的电导率和磁导率的比值:
,使电磁波从介质入射
到边界后,被完全吸收,不被反射。
用FDTD方法推导的2维TE模式和TM模式的电磁波递推表达式 [15],经过计算机的逐步计算,模拟光波在光子晶体中的传播情况,从而得出结果。计算过程中,为了适当控制内存的需求和计算时间,需要恰当的划分计算网格。
介质为圆柱形,半径为r,折射率为n,排列成正方形结构,晶格常数为a,背景材料为空气,折射率为1。相同折射率的圆柱介质排列成2 × 15的基本单元,介质圆柱的折射率在y方向阶梯增加。光波源是波长范围为0.1~5 μm的平面波,计算时的频率抽样点为200,为了不影响光波的传播,包围计算区域的边界是完全匹配层(PML),在平面光波沿y方向通过光子晶体后,测量监测点的透过部分,得出光波的透射系数和透射强度。整个模拟实验使用专门的FDTD软件计算。二维光子晶体的结构图见图1。
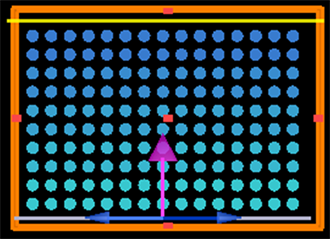
Figure 1. Structure diagram of square photonic crystal of cylindrical medium with increased refractive index stepwise, Every two rows of dielectric cylinders have the same refractive index, which increases in turn along the y direction
图1. 折射率阶梯增加的圆柱介质正方形光子晶体结构图,每两行介质圆柱的折射率相同,折射率沿y方向依次增加
3. 折射率阶梯增加的二维光子晶体对光波的透射率
下面是各个结构的光波透射系数与波长关系图。
图2中所用的光子晶体是10 × 15的结构,圆柱半径 r = 0.2 μm,晶格常数a = 0.6 μm,每2行圆柱介质柱折射率相同,沿y方向折射率阶梯性增加,分别为n = 1.5,2.0,2.5,3.0,3.5。平面波的频率范围是0.1~5 μm,在监测点的频率抽样点为200。由于使用的是平面光波源,光在晶体中传播时,带隙波长范围内的光波不能传播,而且我们计算的是TE波和TM波的总能量,纵轴的总透射能量接近零,说明该波长范围是完全带隙。可以观察到带隙的中心波长为1.1 μm,带隙宽度是0.60~1.50 μm。

Figure 2. r = 0.2 m, a = 0.6 m, transmission coefficient and wavelength relationship
图2. r = 0.2 μm,a = 0.6 μm,透射系数与波长关系图
图3中所用的光子晶体是10 × 15的结构,圆柱半径r = 0.4 μm,晶格常数a = 1.2 μm,每2行圆柱介质柱折射率相同,沿y方向折射率阶梯性增加,分别为n = 1.5,2.0,2.5,3.0,3.5。平面波的频率范围是0.1~5 μm,在监测点的频率抽样点为200。可以观察到带隙的中心波长为2.0 μm,带隙宽度是1.25~2.80 μm。
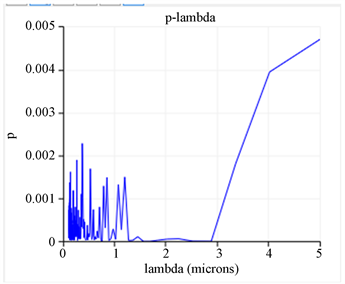
Figure 3. r = 0.4 m, a = 1.2 m, transmitted light energy and wavelength diagram
图3. r = 0.4 μm,a = 1.2 μm,透射光能量与波长关系图
图4中所用的光子晶体是10 × 15的结构,圆柱半径r = 0.4 μm,晶格常数a = 1.6 μm,每2行圆柱介质柱折射率相同,沿y方向折射率阶梯性增加,分别为n = 1.5,2.0,2.5,3.0,3.5。平面波的频率范围是0.1~5μm,在监测点的频率抽样点为200。可以观察到带隙的中心波长为3.0 μm,带隙宽度是2.50~3.40 μm。
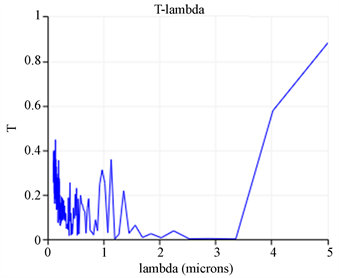
Figure 4. r = 0.4 m, a =1.6 m, transmission coefficient and wavelength relationship
图4. r = 0.4 μm,a = 1.6 μm,透射光透射系数与波长关系图
图5中所用的光子晶体是9 × 9的结构,圆柱半径r = 0.4 μm,晶格常数a = 1.2 μm,每1行圆柱介质柱折射率相同,沿y方向折射率阶梯性增加,分别为n = 1.5,2.0,2.5,构成3行的基本单元,然后重复3次,形成y方向3个周期的结构。入射平面波的频率范围是0.1~5 μm,在监测点的频率抽样点为200。可以观察到带隙的中心波长为1.4 μm,带隙宽度是1.25~1.60 μm。
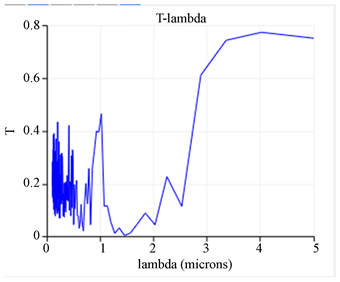
Figure 5. r = 0.4 m, a = 1.2 m, transmission coefficient and wavelength relationship
图5. r = 0.4 μm,a = 1.2 μm,透射光透射系数与波长关系图
图6中所用的光子晶体是10 × 15的结构,圆柱半径 r = 0.4 μm,晶格常数a = 0.8 μm,每2行圆柱介质柱折射率相同,沿y方向折射率阶梯性增加,分别为n = 1.5,2.0,2.5,3.0,3.5。平面波的频率范围是0.1~5 μm,在监测点的频率抽样点为200。可以观察到带隙不明显。
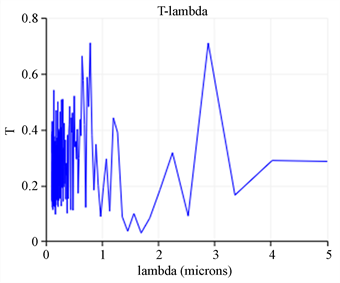
Figure 6. r = 0.4 m, a = 0.8 m, transmission coefficient and wavelength relationship
图6. r = 0.4 μm,a = 0.8 μm,透射光透射系数与波长关系图
为了让数据便于分析,把上述各个光子晶体透射能量(系数)–波长关系中出现的带隙的中心波长和带隙的宽度汇总成表1。

Table 1. Parameters and band gaps of two-dimensional cylindrical photonic crystals with incremental refractive index
表1. 折射率阶梯增加二维圆柱光子晶体的参数和带隙表
图2和图3是同一类型的光子晶体,填充率相同,不同之处是圆柱介质的半径和晶格常数不同,图3的圆柱半径和晶格常数比图2中的要大,带隙的中心波长明显的向长波长方向移动,而且带隙的宽度也变大;图4的填充率比图2和图3的小,晶格常数比图2和图3的大,带隙中心波长向长波长移动明显;图5与图2和图3的填充率相同,但是图5中的折射率在y方向的排列方式是1.5,2.0,2.5,阶梯增加,然后周期性排列,带隙的宽度比图2,图3的变小了;图6中介质圆柱相切,是紧密型光子晶体,带隙不明显。
4. 结论
综上所述,以空气(n = 1.0)为背景,以圆柱形介质构成二维正方形光子晶体结构,每2行的介质折射率相同,沿y方向,折射率阶梯性增加,构成10 × 15的阵列。入射光源是平面波,对通过光子晶体的光波测量透射率。
从图2~图6,以及表1中的数据,得到以下结论:
1) 折射率阶梯增加的紧密型圆柱介质正方形光子晶体,完全带隙不存在,说明当原型介质柱相切时,不能获得完全带隙;
2) 填充率在0.1962到0.3488之间,随着晶格常数增加,带隙的中心波长向长波长方向移动;
3) 在相同的填充率下,折射率阶梯增加,并呈周期性变化时,带隙位置没有变,但是带隙宽度变小。
本文首次提出了这样一种结构:用均匀折射率圆柱介质,构成二维光子晶体,圆柱的折射率在Y方向阶梯性增加。一方面,这样的光子晶体的折射率变化,相对于用电场控制圆柱介质的折射率在半径方向的变化的方法易于实现;另外一方面,可以通过介质柱的折射率在y方向的阶梯变化,通过改变光子晶体的圆柱半径、晶格常数、填充率,可以灵活的调控光子晶体带隙的中心位置和带隙宽度。为人工控制光子晶体的带隙位置和带隙宽度,提供了一个很灵活的手段,为人工设计光子晶体提供了很新的思路。