Rikitake双盘发电机模型的混沌行为分析与数值仿真

Chaotic Behavior Analysis and Numerical Simulation of Rikitake Two-Disk Generator Model

摘要: 通过混沌理论分析和数值仿真方法，对Rikitake双盘发电机模型的混沌行为进行讨论。将Rikitake双盘发电机模型无量纲方程写成三维常系数微分方程组，讨论该系统的耗散性、吸引子的存在性、系统的对称性和不变性。计算系统的平衡点，讨论平衡点的局部稳定性。通过MATLAB编程，从分岔图、最大Lyapunov指数图、吸引子图、时间序列、功率谱等指标分析系统的混沌现象。

Abstract: Through chaos theory analysis and numerical simulation, the chaotic behavior of Rikitake’s two-disk generator model is discussed. The dimensionless equation of Rikitake’s two-disk generator model is written into three-dimensional constant coefficient differential equations, and the dissipation, the existence of attractors, the symmetry and invariance of the system are discussed. The equilibrium point of the system is calculated and the local stability of the equilibrium point is discussed. MATLAB programming was used to analyze the chaotic phenomenon of the system from the bifurcation graph, maximum Lyapunov index graph, attractor graph, time series, power spectrum and other indicators.

1. 引言

随着Lorenz系统的面世，几十年来人们陆续在许多领域发现并分析了混沌现象。混沌是存在于自然界的一种普遍运动形式，是确定系统中产生的不规则运动，具有初值敏感性 [1]。人们在逐渐认识了解混沌的过程中，提出了各种分析方法和判别方法，有助于认识世界发展运行的规律。

地磁理论中最需要说明也是最难说明的关键问题之一是地磁场在长期变化中的极性反转，为此，科学家们提出了运动学发电机反转模型、统计模型、磁流体动力学反转模型和力学模拟模型(圆盘发电机模型) [2]。Rikitake双盘发电机模型是圆盘发电机模型中重要的一种，也是其他模型的重要基础，对其进行研究具有重要意义。

2. 数学模型

双盘发电机模型的无量纲方程 [2] 为：

$\{\begin{array}{l}\frac{\text{d}{x}_1}{\text{d}t}=-\mu x_1+x_2{y}_1\hfill \\ \frac{\text{d}{x}_2}{\text{d}t}=-\mu x_2+x_1{y}_2\hfill \\ \frac{\text{d}{y}_1}{\text{d}t}=\frac{\text{d}{y}_2}{\text{d}t}=1-x_1{x}_2\hfill \end{array}$ (1)

其中 $x_1$ 、 $x_2$ 、 $y_1$ 和 $y_2$ 表示无量纲电流和圆盘的角速度，t是无量纲时间， $\mu >0$ 为参数。

系统(1)可经过化简，化为三维非线性方程组 [3]：

$\{\begin{array}{l}\stackrel{\dot{}}{x}=-\mu x+zy\hfill \\ \stackrel{\dot{}}{y}=-\mu y-ax+xz\hfill \\ \stackrel{\dot{}}{z}=1-xy\hfill \end{array}$ (2)

其中a、 $\mu$ 为系统参数，且有 $\mu >0$ ， $a=2\mu \left(k^2-k^{-2}\right)$ ，k为实常数。

3. 系统耗散性与吸引子的存在性

计算可得，系统(2)的向量场散度为 $\nabla \cdot V=\frac{\partial \stackrel{\dot{}}{x}}{\partial x}+\frac{\partial \stackrel{\dot{}}{y}}{\partial y}+\frac{\partial \stackrel{\dot{}}{z}}{\partial z}=-2\mu <0$ ，所以系统(2)是耗散的，并且以指数形式 $\frac{\text{d}V}{\text{d}t}={\text{e}}^{-2\mu }$ 收敛，收缩为体积元 $V_0{\text{e}}^{-2\mu t}$ ，且当 $t\to \infty$ 时包含系统轨线的每个小体积元以指数率 $-2\mu$ 收缩到0，所有系统的轨线最终会被限制在一个体积为0的极限子集上，且渐近运动将被固定到一个吸引子上，这就说明了吸引子的存在性 [4]。

4. 对称性和不变性

系统(2)具有对称性，即在变换 $\left(X,Y,Z\right)\to \left(-X,-Y,Z\right)$ 下具有不变性，即系统(2)关于Z轴具有对称性，且这种对称性对所有的系统参数均成立 [5]。

5. 平衡点

系统(2)中，x、y和z为表示实际意义的物理量，故x、y和z应为实数，且 $a=2\mu \left(k^2-k^{-2}\right)$ ，由此可令 $\{\begin{array}{l}-\mu x+zy=0\hfill \\ -\mu y-ax+xz=0\hfill \\ 1-xy=0\hfill \end{array}$ ，解方程组 [6] [7] [8] 得 $\{\begin{array}{l}x=\pm k\hfill \\ y=\frac{1}{x}\hfill \\ z=\mu x^2\hfill \end{array}$ 。

故系统(2)有两个平衡点，分别为 $C_1\left(k,\frac{1}{k},\mu k^2\right)$ ， $C_2\left(-k,-\frac{1}{k},\mu k^2\right)$ 。

6. 局部稳定性

由第四节可知，系统(2)具有对称性，故本节只对C₁点进行讨论即可。

系统(2)在C₁点的雅各比矩阵

$J=\left(\begin{array}{ccc}-\mu & z& y\\ -a+z& -\mu & x\\ -y& -x& 0\end{array}\right)=\left(\begin{array}{ccc}-\mu & \mu k^2& \frac{1}{k}\\ \mu k^{-2}& -\mu & k\\ -\frac{1}{k}& -k& 0\end{array}\right)$ (3)

其特征方程为

$\left|\lambda E-J\right|=\left|\begin{array}{ccc}\lambda +\mu & -\mu k^2& -\frac{1}{k}\\ -\mu k^{-2}& \lambda +\mu & -k\\ \frac{1}{k}& k& \lambda \end{array}\right|={\lambda }^3+2\mu {\lambda }^2+\left(k^2+k^{-2}\right)\lambda +2\mu \left(k^2+k^{-2}\right)=0$ (4)

根据劳斯–霍尔维兹判据 [2]，写出劳斯阵列表，表中第一列的元素存在负值，故此时C₁为不稳定的平衡点。

7. 数值仿真

本节对系统(2)的动力学行为进行分析与数值仿真。当固定参数 $\mu =2$ 时，对参数a进行变化，在 $a\in \left[0,50\right]$ 范围内绘制分岔图和最大Lyapunov指数图 [9] [10]，如图1、图2所示。

对比两图，当参数 $\mu =2$ 时，无论参数a如何变化，系统(2)始终是不稳定的，这也与致力于此方面研究的学者们的研究结果一致。为直观展示系统(2)的混沌状态，利用MATLAB软件绘制当 $\mu =2$ ， $a=5$ 时的吸引子图，如图3所示。

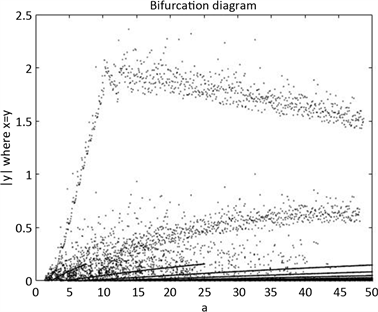
Figure 1. Bifurcation diagram of system (2), when μ = 2, a Î [0,50]

图1. 当μ = 2，a Î [0,50]时系统(2)的分岔图

Figure 2. The maximum Lyapunov index graph of system (2), when μ = 2, a Î [0,50]

图2. 当μ = 2，a Î [0,50]时系统(2)的最大Lyapunov指数图

Figure 3. Attractor diagram when μ = 2, a = 5

图3. 当μ = 2，a = 5时的吸引子图

从图3可以看出，此时两个吸引子均处于不稳定状态，吸引子图呈现出类似洛伦兹系统的蝴蝶形结构，但存在着扭s曲，与洛伦兹吸引子相比较更为复杂。

图4和图5展示了当 $\mu =2$ ， $a=5$ 时的时间序列和功率谱，仿真结果说明此时系统(2)已经进入混沌状态。

Figure 4. Power spectrum of system (2) when μ = 2, a = 5

图4. 当μ = 2，a = 5时系统(2)的功率谱

Figure 5. Time series of system (2) when μ = 2, a = 5

图5. 当μ = 2，a = 5时系统(2)的时间序列

8. 结论

Rikitake双盘发电机模型在经过化简后，可以简化为三维非线性微分方程组。简化后的系统存在两个可调的参数，经过混沌行为理论分析得知，该系统当参数一定时存在混沌现象。从系统的吸引子图中可以发现，轨线从环绕一个吸引子到环绕另一个吸引子的运动轨迹恰如地磁场的极性反转现象，Rikitake双盘发电机模型具有很高的理论研究价值。