一种新型刚柔混合并联机构的动力学研究

Research on the Dynamics of the Novel Rigid and Flexible Mixed Parallel Mechanism

摘要: 随着科技的发展和工业水平的提高，刚柔混合并联机构逐渐成为机构学的研究热点。本文对一种新型刚柔混合欠驱动并联机构进行了研究，基于plücker坐标建立了机构的动力学模型，采用龙格库塔算法对机构的动力学行为进行了数值仿真。研究结果表明，3自由度的刚柔混合并联机构在一个移动副的驱动下具有确定的运动轨迹，机构具有较好的欠驱动特征和容错性。弹性构件的引入有效降低了机构的运动惯性，刚柔混合并联机构可满足机械装备对轻质、高速的需求，在工业中具有良好的应用潜力。

Abstract: With the development of the technology and industry, the rigid and flexible mixed parallel mecha-nism has become a new research hotspot of the field of mechanisms. In this paper, a novel rigid and flexible mixed parallel mechanism is researched. On the basis of plücker coordinates, the dynamic model of the mechanism is developed. Afterwards, the dynamic behaviors are simulated by employing the method of Runge Kutta. The results indicate that the novel rigid and flexible mixed parallel mechanism, of three degrees of freedom, has determinate trajectory driven by one pris-matic joint. It follows that the novel mechanism has better characteristics such as under-driven and fault tolerance. Moreover, the introduced elastic component reduces the mechanism’s motion inertia efficiently. The rigid and flexible mixed parallel mechanisms can meet the rise in demand for low weight and high speed in the fields of machinery equipment and have good potential for applications in the fields of industry.

1. 引言

随着工业探测任务的增加，以串联机构为结构形式的机械臂得到了广泛的应用 [1] [2]。串联机构由刚性连杆和运动副串联组成，其优点是工作空间大、控制灵活、结构简单。串联机构在工业领域的应用提升了机械装备的自动化水平。由于机械臂执行端会累积运动副的误差，致使其运动精度受到了极大影响。在此背景下，并联机构得到了工程师和学者们的广泛关注。与串联机构相比，并联机构具有结构紧凑、刚度大、承载能力强、控制精度高等优点 [3] [4]。

近年来，随着工业复杂性的增加，人们对轻质机构的需求越来越多。国内外的研究者们提出了轻质并联机构。将轻质弹性构件(索或弹簧)替代并联机构中的刚性构件可产生轻质刚柔混合并联机构。弹性构件的引入极大地减轻了整个机构的质量，降低了机构的运动惯性，此类机构在某些需要高速的场合具有良好的应用前景。Marshall [5] 基于3杆9索结构模型首次提出了轻质刚柔混合并联机构，并将这类机构命名为张拉整体并联机构。Arsenault和Clement [6] 提出了3-PUPS张拉整体机构。纪志飞等 [7] 提出了4-SPS刚柔混合并联机构，并探讨了该机构在波浪能收集方面的应用。朱伟等 [8] 对4-SPS张拉整体并联机构的运动学进行了分析。

当刚性并联机构中的刚性构件被索、弹簧等轻质弹性构件替代后，并联机构展现出很好的欠驱动特性。目前，鲜有文献研究此类机构的欠驱动动力学特性。本文以一种新型刚柔混合并联机构为研究对象，将重点研究其欠驱动动力学模型，通过数值算例验证机构的欠驱动动力学行为。论文结果可为轻质刚柔混合并联机构的应用提供理论和数据支持。

2. 机构描述

本文研究的欠驱动刚柔混合并联机构如图1所示，整个机构位于水平平面内，DEF为动平台，底座ABC为静平台，并且DE、EF、DF为刚性连杆。动平台DEF为正三角形，杆DE、DF、EF具有相同的长度l₂。点A、B、C、D、E、F的连接均为平面转动副，构件AD为移动副，BE和FC为弹簧，弹簧刚度分别为K₁和K₂，原长为l₀₁和l₀₂。

建立平面坐标系{A}如图1所示。底座ABC是固定不动的。由于动平台DEF可以在平面内做平移和旋转运动，因此该机构具有3个自由度。

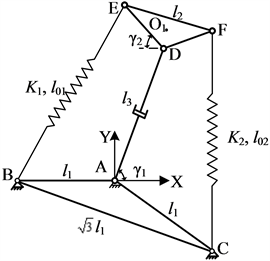
Figure 1. Under-driven rigid and flexible mixed parallel mechanism

图1. 欠驱动刚柔混合并联机构

3. 动力学模型

为了研究机构的欠驱动特性，首先需要建立其动力学模型。由图1可知，静平台ABC的边AB与AC长均为l₁，BC长为 $\sqrt{\text{3}}{l}_1$，动平台DEF的边长为l₂，AD的长度为l₃。弹簧BE、FC的原长分别为l₀₁、l₀₂。取动平台DEF为研究对象，首先确定作用在动平台上的力旋量。线矢量BE、CF、AD的单位方向矢量分别为

$\begin{array}{l}{S}_1=\frac{1}{d_1}\left(l_3{c}_1-l_2{c}_2+l_1\right)i+\frac{1}{d_1}\left(l_3{s}_1+l_2{s}_2\right)j\\ S_2=\frac{1}{d_2}\left(l_3{c}_1+\frac{\sqrt{3}}{2}{l}_2{s}_2-\frac{1}{2}{l}_2{c}_2-\frac{1}{2}{l}_1\right)i+\frac{1}{d_2}\left(l_3{s}_1+\frac{1}{2}{l}_2{s}_1+\frac{\sqrt{3}}{2}{l}_2{c}_2+\frac{\sqrt{3}}{2}{l}_1\right)j\\ S_3=c_{1}i+s_{1}j\end{array}$ (1)

式(1)中d₁和d₂分别表示矢量BE、CF的长度，i和j分别表示坐标系X、Y方向的单位向量。s_i表示的是sinγ_i，c_i表示的是cosγ_i，i=1, 2。用矢量k表示矢量i和j的叉积，则线矢量BE对O₁的线距为

$\begin{array}{c}{S}_{01}=\frac{1}{d_1}{S}_{O_{1}B}\times S_{BE}\\ =\frac{1}{d_1}\left[\frac{1}{2}{l}_2{l}_3\left(c_1{s}_2-c_2{s}_1+\frac{\sqrt{3}}{3}{s}_1{s}_2-\frac{\sqrt{3}}{3}{c}_1{c}_2\right)+\frac{\sqrt{3}}{6}{l}_2^2+l_1{l}_2\left(\frac{1}{2}{s}_2-\frac{\sqrt{3}}{6}{c}_1\right)\right]k\end{array}$ (2)

线矢量CF对O₁的线距为

$\begin{array}{c}{S}_{02}=\frac{1}{d_2}{S}_{O_{1}C}\times S_{CF}\\ =\frac{1}{d_2}[\left(\frac{\sqrt{3}}{3}{c}_1{c}_2-\frac{5}{12}{s}_{1}s{}_2+\frac{1}{2}{s}_1{c}_2\right)l_2{l}_3+\frac{1}{2}\left(\frac{\sqrt{3}}{3}{c}_2-s_2\right)l_1{l}_2-\frac{\sqrt{3}}{6}{l}_2^2]k\end{array}$ (3)

线矢量AD对O₁的线距为

$\begin{array}{c}{S}_{03}=\frac{1}{l_3}{S}_{O_{1}A}\times S_{AD}\\ =\left[\frac{\sqrt{3}}{6}{l}_2\left(s_1{s}_2-c_1{c}_2\right)-\frac{1}{2}{l}_2\left(s_1{c}_2-c_1{s}_2\right)\right]k\end{array}$ (4)

因此作用在平台DEF上的力旋量为

$\begin{array}{c}\cancel{F}=f_1{\cancel{S}}_1+f_2{\cancel{S}}_2+f_3{\cancel{S}}_3\\ =\left(f_1{S}_1+f_2{S}_2+f_3{S}_3\right)+\in \left(f_1{S}_{01}+f_2{S}_{02}+f_3{S}_{03}\right)\end{array}$ (5)

式(5)中f₁、f₂、f₃分别弹簧BE、CF和驱动副AD施加在平台DEF的力， $\in$ 为对偶标识符。动平台DEF的运动可分解为随质心的平动和绕质心的转动，其平动速度为

$v=\frac{\text{d}\left(l_3{c}_1-\frac{1}{2}{l}_2{c}_2+\frac{\sqrt{3}}{6}{l}_2{s}_2\right)}{\text{d}t}i+\frac{\text{d}\left(l_3{s}_1+\frac{1}{2}{l}_2{s}_2+\frac{\sqrt{3}}{6}{l}_2{c}_2\right)}{\text{d}t}j$ (6)

向量O ₁ F 在平面内绕O₁点转动的转动速度为

$\omega =\frac{\text{d}\theta }{\text{d}t}=\frac{d\left(2\pi -\arctan \left(c_2/s_2\right)\right)}{\text{d}t}$ (7)

其中q为向量O ₁ F 的转角，方向由右手定则确定。因为动平台DEF绕质心的转动速度与平台上任一点绕质心的转动速度相等，故动平台DEF绕质心的转动速度也为w。因此动平台质心运动旋量的plücker坐标为

$\left(\begin{array}{c}v\\ \omega \end{array}\right)=\left(\begin{array}{c}\frac{\text{d}\left(l_3{c}_1-\frac{1}{2}{l}_2{c}_2+\frac{\sqrt{3}}{6}{l}_2{s}_2\right)}{\text{d}t}i+\frac{\text{d}\left(l_3{s}_1+\frac{1}{2}{l}_2{s}_2+\frac{\sqrt{3}}{6}{l}_2{c}_2\right)}{\text{d}t}j\\ \frac{d\left(2\pi -\arctan \left(c_2/s_2\right)\right)}{\text{d}t}\end{array}\right)$ (8)

假设动平台DEF每根杆的质量为m，则动平台绕质心的转动惯量为

$I=3\left[\frac{m}{12}{l}_2^2+m{\left(\frac{\sqrt{3}}{6}{l}_2\right)}^2\right]$ (9)

所以动平台运动的动力学方程为

${\displaystyle \underset{i=1}{\overset{3}{\sum }}{f}_i{S}_i}+\in {\displaystyle \underset{i=1}{\overset{3}{\sum }}{f}_j{S}_{0j}}=\left(\begin{array}{cc}3m& 0\\ 0& I\end{array}\right)\frac{\text{d}\left(v+\in \omega \right)}{\text{d}t}$ (10)

给定驱动副AD的输入

$l_3=t+10$ (11)

将式(11)代入式(10)，可得

${\displaystyle \underset{i=1}{\overset{3}{\sum }}{f}_i{S}_i}+\in {\displaystyle \underset{i=1}{\overset{3}{\sum }}{f}_j{S}_{0j}}=\left(\begin{array}{cc}3m& 0\\ 0& I\end{array}\right)\frac{\text{d}\left(v+\in \omega \right)}{\text{d}{l}_3}$ (12)

式(12)即为图1所示的欠驱动刚柔混合并联机构的动力学模型。从式(12)中可以看出，机构的动力学模型是一个二阶的微分方程组，确定初始条件，利用龙格–库塔法便可求得此模型的数值解。

4. 数值算例

4.1. 初始条件

在图1中，欠驱动混合并联机构的参数如下：杆长l₁ = 9.77 m ，l₂ = 4.80 m ，l₃ = 10 m ，弹簧BE的刚度K₁ = 10 N/m，CF的刚度K₂ = 15 N/m，上平台连杆的质量均为m = 4 kg 。

为了对求解方程(12)，必须给定其初始条件。对于动平台DEF来说，在驱动副AD未施加驱动力之前，机构处于静止状态。此时平台DEF所受合力及合力矩为零，有

$\left(f_1{S}_1+f_2{S}_2+f_3{S}_3\right)+\in \left(f_1{S}_{01}+f_2{S}_{02}+f_3{S}_{03}\right)=0$ (13)

为了简化计算，不妨设 $l_{01}=l_{02}=0$，此时求解式(12)可得到γ₁和γ₂的值如表1所示。

Table 1. Values of γ1and γ2

表1. γ₁和γ₂数值

在二维空间里，虚数解无物理意义。因此从表1可以看出，给定驱动副AD的长度，此平面张拉整体并联机器人机构有4个平衡位置。因为机构可以从任何一个静止状态开始运动，所以表1中的任何一组实数解均可作为式(12)的初始条件。本文选取第二组解。在开始运动时，机构的平移速度和转动速度均为零。所以方程(12)的初始条件为

$\begin{array}{l}{\gamma }_1=2.3617,{\gamma }_2=0.1793\\ \frac{\text{d}{\gamma }_1}{\text{d}{\mathcal{l}}_3}=\frac{\text{d}{\gamma }_2}{\text{d}{\mathcal{l}}_3}=0\end{array}$ (14)

4.2. 动力学仿真

考虑初始条件式(14)，利用4阶龙格–库塔算法可求得式(12)的数值解如图2所示。

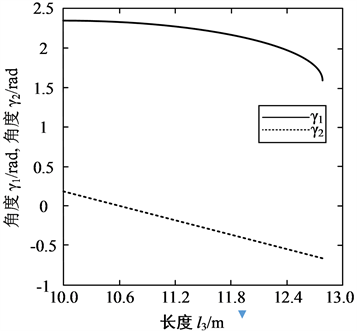
Figure 2. Numerical solutions to the dynamic equations

图2. 动力学方程的数值解

图2表示的是角度γ₁和γ₂随驱动副AD长度l₃的变化规律。根据式(1)可知，在二维平面内，确定γ₁和γ₂及驱动副AD的值便可唯一确定动平台DEF的位置及姿态。因此根据图2的结果便可以得到在驱动副AD的作用下，动平台的运动情况。动平台DEF在移动副AD的作用下，具有确定的运动轨迹。但因为此系统具有3个自由度，因此它是一种欠驱动非线性机构，并且能在移动副AD的驱动下，稳定地运动。如果将驱动副AD看作系统的输入，动平台的质心看作系统的输出，那么对于此3自由度系统，只需给定一个输入便可确定系统的输出，因此张拉整体并联机器人具有欠驱动、容错性等特点。

图3所示的是平面张拉整体并联机构在驱动副AD的作用下运动序列。从图3可以看出，动平台DEF在移动副AD的作用下，具有确定的运动轨迹。但因为此系统具有3个自由度，因此它是一种欠驱动非线性机构，并且能在移动副AD的驱动下，稳定地运动。如果将驱动副AD看作系统的输入，动平台的质心看作系统的输出，那么对于此3自由度系统，只需给定一个输入便可确定系统的输出，因此张拉整体并联机器人具有欠驱动、容错性等特点。

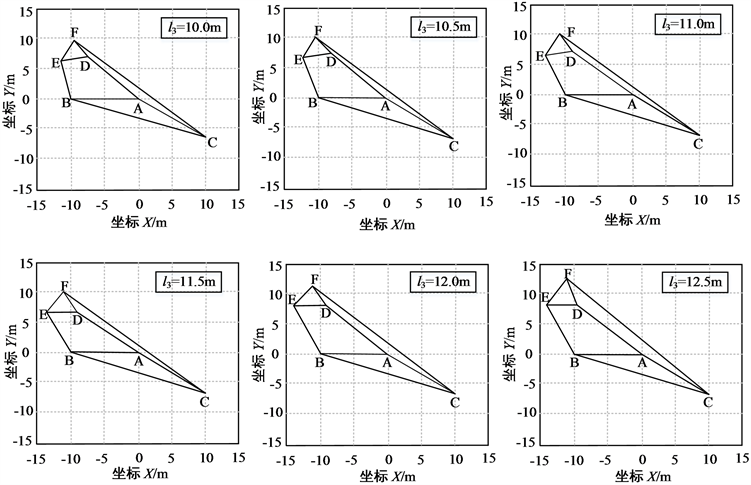
Figure 3. Moving sequence of the mechanism

图3. 机构的运动序列

5. 结论

本文对一种新型的欠驱动刚柔混合并联机构进行了动力学分析，主要结论如下：

1) 将传统并联机构的刚性构件用索或弹簧等弹性构件替代后，机构的运动惯性得到了有效降低，轻质刚柔混合并联机构在一些需要高速的场合具有良好的应用前景；

2) 基于plücker坐标建立的机构动力学模型具有结构形式紧凑、物理意义明确等特点；

3) 本文研究的刚柔混合并联机构具有3个自由度，在一个移动副的驱动下，机构整体具有确定的运动轨迹。因此所研究机构具有良好的欠驱动特性。

基金项目

福建省自然科学基金资助项目(2018J05088)；福建省中青年教师教育科研项目资助(JAT170319)；集美大学博士科研启动基金资助(ZQ2017005)。