1. 引言
复杂形状的构件在航空航天工业中广泛应用于加固结构中。通过弯曲形状加固的机翼由于应力过强或外力冲击易产生损坏,这些损坏对于客机正常航行和乘客安全极有可能造成灾难,如美国航空公司587航班空难,造成严重的财产损失与人员伤亡。及时识别定位,对其进行维护,这对航空正常运行有重大意义。因此,为了保证空中运输安全,需要定期对飞机进行检测,及时排查有安全隐患的部件 [1]。
超声导波传播特性最早在20世纪初被用于实验研究,其研究方法可分为两类——解析法和数值法。弹性波 [2] 是H. Lamb在1917年发现在板中传播的波,与Rayleigh共同推出的Rayleigh-Lamb超越方程对Lamb波在导体中传播的多模态特性与频散特性进行解析分析。Mindlin板理论可近似的描述Lamb波在板结构中的传播过程,该方法可用于研究压电晶片与波导耦合结构。上述解析方法适用于简单结构。目前,边界元法 [3]、有限元法、有限差分法 [4]、半解析有限元法等数值方法都用于对导波的传播研究。其中,有限元法将连续的弹性体划分为若干子单元,通过边界上的节点将其连接,利用变分原理得到弹性体总体运动方程,选择适当方法求解即可得到各离散点的解。Mencik J M和Ichchou M N [5] 通过有限元方法提出了一种复杂波导体结构中超声导波频散曲线的计算方法。
复杂形状的构件结构复杂,缺陷部位可能出现反射折射,给测量造成一定的困难。目前有多种检测缺陷的方法 [6],其中超声波缺陷检测具有指向性强、能量损失小、传播距离远、效率高、成本低等优点,被认为是目前最有效的缺陷检测手段 [7] [8]。本文建立激光作用于90度弯曲相交界面模型,对其激发产生导波的传播特性进行了研究。脊部的温度分布保证了声部在热弹机制的激发。声波除了沿脊部传播,同时向相交界面扩散传播。通过对脊部等间隔取点,观察其波形、B-Scan图,并对其功率谱进行积分研究了导波传播过程中能量的变化。
2. 理论研究
基于热弹性理论,建立激光作用于弯曲界面脊部,激发产生导波的理论模型。考虑到激光作用于弯曲界面的热扩散和导波的传播特性,建立三维模型,其示意图如图1所示。其中,两界面弯曲相交角度为90度,在弯曲界面的脊部传播的声波仅仅存在瑞利波 [9]。
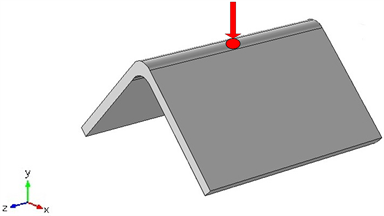
Figure 1. Schematic diagram of laser irradiated on curved intersection interface
图1. 激光辐照弯曲相交界面三维模型示意图
脉冲激光垂直辐照到弯曲界面脊部表面后,其能量被表层迅速吸收。根据能量守恒的原理,材料表面吸收激光能量后,将引起表层温度的升高及表层局部的体积膨胀,从而产生瞬态位移场,热传导方程如式(1)所示。模拟中采用各向同性的铝板材料,材料参数如表1所示,超声波的传播满足Navier-Stokes方程 [10],如方程(2)所示
(1)
(2)
式中,ρ,cv和k分别表示热扩散系数、密度和定容比热容,
表示t时刻的温度分布,
表示热弹耦合系数,其中αT是线性热膨胀系数,λ和μ是Lamé常数。
激光作为热流边界作用于相交界面脊部,非激光辐照区域按绝热条件处理。在此,假设弯曲相交界面脊部表面存在一个随时间变化的外部热源,激光辐照区的边界条件满足
(3)
式中,A(T)是材料表面的吸收率,I0是脉冲激光的峰值功率密度。f(x, z)和g(t)分别是脉冲激光能量的空间和时间分布函数,其表达式为
(4)
(5)
其中,x0和z0表示激光作用的中心位置,RG为脉冲激光作用半径,t0为激光脉冲宽度。由于模型受到支撑与扣件约束,现实情况中边界条件较复杂。本文为了研究方便,排除其他因素的影响,设置x-y平面上的两个界面为低反射边界,其他界面采用自由边界条件。
(6)
式中,n是垂直表面的单位向量,σ是应力张量,I是单位张量。模型初始温度为室温,初始的位移为零。
(7)
(8)
考虑到时空分辨率,时间步长设置为2 ns。在辐照区域划分精细的网格,网格大小设置为5 μm,而远离激光辐照网格最大为100 μm。模型的尺寸为z方向5 mm,厚度为0.24 mm。相交界面曲率半径为4 mm。激光线源的半宽为RG = 0.1 mm,激光脉冲的上升时间是t0 = 10 ns。忽略铝材料参数对温度的依赖性,常温下使用的铝板材料的参数如表1所示。
3. 结果与讨论
采用上文理论建立有限元模型对点源激光在模型表面激发超声导波进行分析,热源位于z = 2.5 mm处,方向沿负y轴方向。脉冲激光以表面热源的形式加载相交界面脊部,其辐射能量I0为1 × 1011 W/m2。图2为模型表面温度场示意图,可以看出温度升高区域主要是热源辐照的中心点附近,温升约为20 K,由此看出声波产生处于热弹机制。激光辐照的边缘区域,温度迅速降低;远离激光辐照区域,温度保持室温不变。

Figure 2. Temperature field at the ridge of laser irradiation
图2. 激光辐照弯曲相交界面温度场
相交弯曲模型的表面应力示意图如图3所示。从图中可以看出点源激光激发的声表面波同时沿弯曲脊方向和侧表面传播。时间t = 0 μs时,模型中无激光作用,无声波传播。T = 0.4 μs时,激光作用区域(脊部)应力最大,红色代表应力值最大;声波除了沿着脊部传播,同时沿侧面扩散传播,且沿脊部传播的导波最强。t = 0.8 μs时,声波沿侧面继续向外扩散传播。根据能守恒定律,沿侧面传播的声波幅度逐渐衰减。脊部传播的导波保持不变。在t = 1.2 μs时,沿脊部传播的声波到达边界,由于边界x-y平面设置的低反射边界条件,因此观察不到声波。沿侧面传播的声波振幅持续减弱。
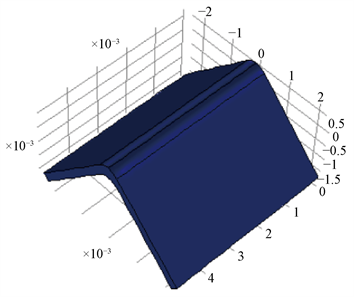 (a) t = 0 μs
(a) t = 0 μs 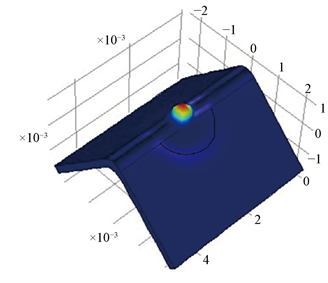 (b) t = 0.4 μs
(b) t = 0.4 μs  (c) t = 0.8 μs
(c) t = 0.8 μs  (d) t = 1.2 μs
(d) t = 1.2 μs
Figure 3. The diagram of guide wave propagation
图3. 相交弯曲模型的表面应力示意图
在模型脊上0至5 mm取点,等间隔为0.05 mm,导出每个点在y方向上的竖直位移,结果如图4所示。其中横坐标为时间,纵坐标为z方向上位置。z方向2.25~2.75 mm处为激光作用区域,位移最大。随时间推移,声波在z = 2.5 mm处向两侧沿z轴的正负方向传播。蓝色部分是激光源照射区域,始终处于最大位移。由于其结构的特殊性,沿脊部传播的声波,能量集中,衰减很小 [9]。弯曲相交界面的相交角度为90度,因此在脊上传播声波只有瑞利波,铝材料中的速度约为3000 m/s,由此估算声波从激光的边缘位置传播到模型边约为0.81 μs,与仿真结果吻合。

Figure 4. The B-scan of the guided waves on model spine
图4. 模型脊上位移情况的B-scan图
在脊部激光加载区域一侧等间隔取5个点,如图5所示绘制波形图。黑色箭头表示采样方向,即导波传播方向。随着采样点远离激光加载区,声波起震时间越晚,但是导波在传播过程中峰值基本无衰减,即沿脊背上传播的声波能量不损失。此特性可用于后期检测导波在相交界面脊部传播是否有损伤。为了更好的研究导波能量变化,对沿脊部传播的导波能量进行分析。
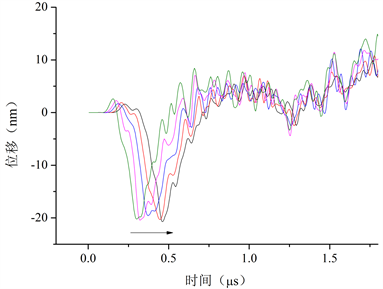
Figure 5. The waveforms at the ridge of curved intersection interface
图5. 弯曲相交界面脊部不同位置处的声波波形
在上述研究的基础上,对扫查得到的位于脊部的波形的功率谱进行积分,得到了声波沿脊部传播过程中的能量变化,如图6所示。横坐标表示z轴位置,纵坐标表示归一化的能量值。该图中可以看出,在z轴2.25 mm~2.75 mm位置能量值最大,该区域为激光加载区,与图4结论吻合。在0 mm~2.25 mm与2.75 mm~5 mm这两个区域,声波能量与激光作用区能量相比非常小,基本不发生变化。为了更好的观察声波能量的变化,对0.2 mm~2.0 mm区间能量进行放大处理。发现其能量值在0.1附件波动变化,波动范围很小,在此认为声波能量基本保持不变,与前文结论一致。

Figure 6. The energy of guided waves on curved intersection interface
图6. 弯曲相交界面声波能量分布
4. 总结
本文研究了激光作用于90度弯曲相交界面导波的传播特性。首先,建立激光作用于90度弯曲相交界面脊部模型。在热源辐照点附近,温升为20 K,保证了声波在热弹机制的激发。导波除了沿脊部传播,同时向相交界面侧面扩散传播。根据能守恒定律,沿侧面传播的声波能量逐渐衰减。其次,通过对脊部等间隔取点,z方向2.25 mm~2.75 mm处为激光作用区域,位移最大。相交界面的相交角度为90度,因此在脊上传播声波只有瑞利波。随着采样点远离激光加载区,声波起震时间越晚,并且在传播过程中峰值基本无衰减。最后,对位于脊部声波波形的功率谱进行积分,激光作用区能量最大,传播区域能量值在0.1附件很小范围波动,在此认为声波能量基本保持不变。
基金项目
国家自然科学基金项目“基于激光超声的楔体缺陷检测与评估方法研究”(11704096)。