一类水波方程的精确解

The Exact Solutions for a Class of Shallow Water Equation

摘要: 本文研究了一类水波方程如浅水波方程及其推广形式、修正的KdV方程等，分别利用试探方程法、双曲正切函数展开法，以及Jacobi椭圆函数展开法构造并求得了他们的精确解。

Abstract: In this paper, a class of water wave equations such as shallow water equation and its extended form, as well as modified KdV equation are studied. The trial equation method, hyperbolic tangent function expansion method, and Jacobi elliptic function expansion method are used respectively to construct and obtain the exact solutions.

1. 引言

经过50多年的不断研究和探索，人们对非线性问题的研究取得了不少深入的成果，寻求非线性发展方程的精确解已经成为偏微分方程研究的一个重要课题。近年来，人们对于非线性发展方程的精确解的研究已有了很大进展，提出了许多行之有效的方法。例如，著名的反散射方法、混合指数法、齐次平衡法、Jacobi椭圆函数展开法、双曲正切函数展开法等等，都是构造一些非线性发展方程解析解的有效方法 [1] - [10]。通过这些方法获得的非线性发展方程的诸多精确解，合理地解释了相关的自然现象，极大地推动了相关学科如物理学、力学、应用数学以及工程技术的发展。

本文考虑浅水波方程：

$u_t-u_{xxt}+3u{u}_x-2u_x{u}_{xx}-u{u}_{xxx}=0$ (1)

及其推广形式：

$u_t-u_{xxt}+\left(p+1\right)u^p{u}_x-p{u}^{p-1}{u}_x{u}_{xx}-u^p{u}_{xxx}=0$ (2)

和修正的KdV方程：

$u_t+\alpha u^2{u}_x+u_{xxx}=0$ (3)

本文利用试探方程法、双曲正切函数展开法及其推广形式，以及Jacobi椭圆正弦函数展开法构造并求得了他们的精确解。

2. 定理的证明

2.1. 浅水波方程(1)的精确解——试探方程法

令

$u\left(x,t\right)=\phi \left(\xi \right)$， $\xi =x-ct$ (4)

将(4)代入(1)得

$-c{\phi }^{\prime }+c{\phi }^{‴}+3\phi {\phi }^{\prime }-2{\phi }^{\prime }{\phi }^{″}-\phi {\phi }^{‴}=0$ (5)

两边积分得

$-2c\phi +2c{\phi }^{″}+3{\phi }^2-2\phi {\phi }^{″}-{{\phi }^{\prime }}^2=2A$ (6)

其中A为积分常数。(6)式两边同时乘以 ${\phi }^{\prime }$ 积分得：

$\left(\phi -c\right){{\phi }^{\prime }}^2={\phi }^3-c{\phi }^2-2A\phi -B$ (7)

其中B为积分常数。根据(7)式，我们不妨假设

${{\phi }^{\prime }}^2=a_0+a_1\phi +a_2{\phi }^2$ (8)

其中 $a_0,a_1,a_2$ 待定的常数，并将其代入到方程(7)中去，整理并求解得：

$\{\begin{array}{l}{a}_2=1\\ a_1=0\\ a_0=-2A\\ c{a}_0=B\end{array}$

又由(8)可得

$2{\phi }^{″}=a_1+2a_2\phi$ (9)

将 $a_1$ 和 $a_2$ 代入到(9)中去，求解可得：

$\phi =c_1{\text{e}}^{\xi }+c_2{\text{e}}^{-\xi }$ (10)

其中 $c_1$， $c_2$ 为任意的常数。

定理1 浅水波方程(1)具有如下精确解：

$u\left(x,t\right)=c_1{\text{e}}^{\left(x-ct\right)}+c_2{\text{e}}^{-\left(x-ct\right)}$ (11)

取 $c_1=0$， $c_2=1$，运用mathematica数学软件可得如图1所示的波形图：

Figure 1. The oscillogram with parameters $c_1=0,c_2=1$

图1. $c_1=0,c_2=1$ 时的波形图

注：类似可得浅水波方程的推广形式(2)具有如下形式

$u\left(x,t\right)=c_1{\text{e}}^{\left(x-ct\right)}+c_2{\text{e}}^{-\left(x-ct\right)}$ (12)

的精确解，其中 $c_1$， $c_2$ 为任意常数。

2.2. 修正的KdV方程的精确解——双曲正切函数展开法

令

$u\left(x,t\right)=\phi \left(\xi \right)$， $\xi =kx-ct$ (13)

在此变换下，我们有

$-c{u}^{\prime }+\alpha u^2{u}^{\prime }+k^2{u}^{‴}=0$ (14)

假设方程(3)具有如下双曲正切函数多项式形式的解

$u\left(\xi \right)={\displaystyle \underset{i=0}{\overset{m}{\sum }}{a}_i}{f}^i$， $f=\tanh \left(\xi \right)$ (15)

其中系数 $a_i\left(i=0,\cdots ,m\right)$ 为待定参数。根据双曲正切函数的性质，我们有：

$f^{\prime }=1-f^2$ (16)

平衡方程(14)中线性最高阶导数项 $k^2{u}^{‴}$ 与最高阶非线性项 $\alpha u^2{u}^{\prime }$ 的幂次，根据齐次平衡原则有 $2m+m+1=m+3$，从而

$m=1$

将上式代入到(15)中，从而方程(3)的拟解的形式为

$u=a_0+a_{1}f$ (17)

将其代入到方程(14)中，整理得：

$-c{a}_1-2k^2{a}_1+\alpha a_0^2{a}_1+2\alpha a_0{a}_1^{2}f+\left(c{a}_1+8k^2{a}_1-\alpha a_0^2{a}_1+\alpha a_1^3\right)f^2$ $-2\alpha a_0{a}_1^2{f}^3+\left(-6k^2{a}_1-\alpha a_1^3\right)f^4=0$

由 $f,f^2,f^3,f^4$ 线性无关，我们有如下代数方程组成立：

$\{\begin{array}{l}-c{a}_1-2k^2{a}_1+\alpha a_0^2{a}_1=0\\ 2\alpha a_0{a}_1^2=0\\ c{a}_1+8k^2{a}_1-\alpha a_0^2{a}_1+\alpha a_1^3=0\\ -6k^2{a}_1-\alpha a_1^3=0\end{array}$ (18)

求解该方程组得：

(1) $a_1=\frac{\sqrt{3c}}{\sqrt{\alpha }}$， $k=\frac{i\sqrt{c}}{\sqrt{2}}$，

(2) $a_1=\frac{\sqrt{3c}}{\sqrt{\alpha }}$， $k=-\frac{i\sqrt{c}}{\sqrt{2}}$，

(3) $a_1=-\frac{\sqrt{3c}}{\sqrt{\alpha }}$， $k=-\frac{i\sqrt{c}}{\sqrt{2}}$，

(4) $a_1=-\frac{\sqrt{3c}}{\sqrt{\alpha }}$， $k=\frac{i\sqrt{c}}{\sqrt{2}}$，

其中 $\left(a_0=0\right)$。

将其代入到方程(3)中，整理可得该方程的精确解如下：

$u\left(x,t\right)=\pm \frac{\sqrt{3c}}{\sqrt{\alpha }}\tanh \left(\xi \right)$. (19)

其中 $\alpha$ 为任意常数，c为波速。

定理2 修正的KdV方程方程(3)具有如下形式：

$u\left(x,t\right)=\pm \frac{\sqrt{3c}}{\sqrt{\alpha }}\tanh \left(kx-ct\right)$ (20)

的精确解。

运用mathematica数学软件作图可得如图2所示的波形图：

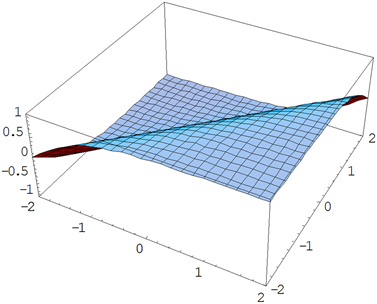
Figure 2. The oscillogram with parameters $\alpha =3c$

图2. $\alpha =3c$ 时的波形图

2.3. 修正的KdV方程的精确解——Jacobi椭圆函数展开法

对于方程(3)，我们假设其行波解为：

$u\left(\xi \right)={\displaystyle \underset{i=0}{\overset{m}{\sum }}{a}_i}{S}^i$ (21)

其中 $S=sn\left(\xi ,r\right)$。这里正整数m和实常数 $a_i\left(i=1,2,\cdots ,m,a_m\ne 0\right)$ 待定。

平衡方程(3)中线性最高阶导数项与非线性项的次数，得 $m+3=3m+1$，即 $m=1$，于是方程(3)的解可设为：

$u=a_0+a_{1}S$ (22)

可验证方程(3)各项的秩全为奇数(秩同类)，从而有：

$S^{\prime }=CD$， $C^{\prime }=-SD$， $D^{\prime }=-r^{2}SC$， $u^{\prime }=a_1{S}^{\prime }$

$u^{″}=-a_{1}S{D}^2-a_1{r}^{2}S{C}^2$， $u^{‴}=CD\left(-a_1-a_1{r}^2+6a_1{r}^2{S}^2\right)$. (23)

其中 $C=cn\left(\xi ,r\right)$， $D=dn\left(\xi ,r\right)$。

将(23)式代入到方程(3)中并整理得：

$CD\left(-c{a}_1-k^2{a}_1-k^2{r}^2{a}_1+\alpha a_0^2{a}_1+2\alpha a_0{a}_1^{2}S+\left(6k^2{r}^2{a}_1+\alpha a_1^3\right)S^2\right)=0$ (24)

由 $1,S,S^2$ 线性无关，我们得到一个非线性的代数方程组如下：

$\{\begin{array}{l}-c{a}_1-k^2{a}_1-k^2{r}^2{a}_1+\alpha a_0^2{a}_1=0\\ 2\alpha a_0{a}_1^2=0\\ 6k^2{r}^2{a}_1+\alpha a_1^3=0\end{array}$ (25)

求解得：

$a_1=-\frac{\sqrt{6}\sqrt{c+\frac{c}{-1-r^2}}}{\sqrt{\alpha }}$， $k=-\frac{\sqrt{c}}{\sqrt{-1-r^2}}$，或 $a_1=-\frac{\sqrt{6}\sqrt{c+\frac{c}{-1-r^2}}}{\sqrt{\alpha }}$， $k=\frac{\sqrt{c}}{\sqrt{-1-r^2}}$

或 $a_1=\frac{\sqrt{6}\sqrt{c+\frac{c}{-1-r^2}}}{\sqrt{\alpha }}$， $k=-\frac{\sqrt{c}}{\sqrt{-1-r^2}}$，或 $a_1=\frac{\sqrt{6}\sqrt{c+\frac{c}{-1-r^2}}}{\sqrt{\alpha }}$， $k=\frac{\sqrt{c}}{\sqrt{-1-r^2}}$

其中 $a_0=0$。

将上式代入到方程(3)中，可得椭圆正弦周期波解：

$u\left(x,t\right)=\pm \frac{\sqrt{6}\sqrt{c+\frac{c}{-1-r^2}}}{\sqrt{\alpha }}sn\left(\xi ,r\right)$. (26)

在(26)中令 $r\to 1$，可以得到方程(3)的孤立波解：

$u\left(x,t\right)=\pm \frac{\sqrt{6c}}{\sqrt{2\alpha }}sn\left(\xi ,1\right)$. (27)

其中 $\alpha$ 为任意常数，c为波速。

定理3修正的KdV方程方程(3)具有如下形式的椭圆正弦周期波解：

$u\left(x,t\right)=\pm \frac{\sqrt{6}\sqrt{c+\frac{c}{-1-r^2}}}{\sqrt{\alpha }}sn\left(\left(x\text{,}t\right),r\right)$. (28)

令 $r\to 1$，方程(3)的孤立波解为：

$u\left(x,t\right)=\pm \frac{\sqrt{6c}}{\sqrt{2\alpha }}sn\left(\left(x\text{,}t\right),1\right)$. (29)

其中 $\alpha$ 为任意常数，c为波速。

运用mathematica数学软件作图可得如图3所示的波形图：

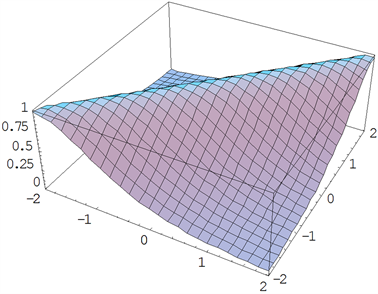
Figure 3. The oscillogram with parameters $\alpha =3c$

图3. $\alpha =3c$ 时的波形图

致谢

在此对本文提出修改意见的专家表示感谢！对本文的资助项目表示感谢！

基金项目

本文得到中国河南省科技攻关项目(项目号：172102210271)和中国河南理工大学博士基金项目(项目号：B2018-50)的资助。