1. 引言
1.1. 研究背景
2014年公布的IPCC第5次报告指出,全球降水将会呈现“干者愈干,湿者愈湿”的趋势,而全球变暖也是近百年来最主要的气候特征,这使得世界范围内很多地区的各种气象要素都发生了很大的变化,直接导致全球降水分布发生改变,同时在全球变暖背景下研究降水量时空分布,可以在某种程度上反映全球气候变化与迁移的情况 [1]。降水量是极为重要的气象要素可以用来描述某一地区的气候特征。卫星遥感获得的降水数据,是目前进行区域降水时空分析的重要数据来源,因为卫星数据具有分辨率高、分布连续等优点 [2] [3]。降水时空分布是气象、气候、水文、生态以及经济、农业和其他相关学科研究的基础和必要支撑,而降水时空分布的变化不止对地表河流径流量有直接影响,同时对研究水资源也有很大的影响,其可以为洪涝灾害的防治预测提供参考 [4] [5] [6] [7] [8]。此外降水分布关乎农业发展和粮食安全,所以在全球变暖的背景下研究多尺度降水分布特征对全球气候变化以及水资源的研究至关重要。
目前采集降水观测信息的手段主要有以下几种:地面雨量计、地基雷达和卫星遥感探测信息。一方面,由地面雨量计和地基雷达观测采集到的降水资料的准确度较高,也是目前较为成熟的手段,但其空间分布不均匀,数据类型为离散型数据,所以目前被用于进行局部地区的降水观测,加之气象台站分布的密度较低,所以想要获得大范围的或者说全球的比较准确的降水信息时有一定难度的,而且就算是在给定的局部小区域内,想要获得任何一处的降水信息也是不可能的。
另一方面,卫星遥感的优点是在全球或者给定的大区域内进行连续而非间断式的观测,获取得到时间分辨率很高的观测数据卫星遥感,因此可以弥补上述两种观测手段的不足。
1.2. 研究现状
四川省位于中国的西南地区,地形复杂,海拔差异巨大,有丘陵、高原、冰川、草原等地形地貌,由于独特的地理特征,其气候变化与全球以及中国大部分地区呈现相反的趋势 [9] [10] [11] [12]。至上个世纪80年代以来,国内外很多学者都对四川省降水变化进行了很多研究,如陈海山等研究中国近50年不同区域极端降水事件变化特征的季节性差异,分析得出西南地区极端降水事件发生频次较高,年极端降水事件从长期来看有减少趋势 [13]。罗玉等研究了1961~2015年四川省156个气象台站的汛期极端降水指数时空变化特征,发现55年间汛期的极端降水指数在大部分地区呈现增加趋势且有明显周期变化 [14]。邵远坤等分析了四川盆地的降水特征 [15]。王真等利用1971~2018年四川省35个气象站的逐日降水资料,对四川省极端降水指数进行研究发现:(1) 极端降水指数随时间变化不显著,但是随经度、海拔高度有着明显的变化,其中只有降水强度是随时间呈现明显增大趋势,并且其突变发生在上个世纪的八九十年代。(2) 川西极端降水事件多发,四川中部地区逐渐变得干旱,四川东部地区发生洪涝可能性增加 [16]。张顺谦等(2011)利用1961~2009年四川省143个气象站的逐日降水资料,发现近50年来极端降水日数是在减少,但极端降水量却是有些微增加,极端降水指数都有着5~8年的震荡周期,且大部分站点的指数是没有突变的 [17]。
对于大渡河流域的研究,程珂等研究了大渡河流域年径流量和降水量之间的关系 [18]。吴付华等通过研究大渡河周围洪水、暴雨的成因,分析统计大渡河流域暴雨、洪水的时间以及空间分布,总结该流域暴雨、洪水的特征 [19]。刘佳等通过对大渡河流域极端降水指数进行研究,发现大渡河流域的极端降水指数为波动增加的稳定趋势,多年平均值有着统一的分布特征,即由西北向东南方向逐渐增多 [20]。孙文慧等根据1960~2010年逐日降水资料,研究了大渡河上游汛期降水的时空分布,发现大渡河上游汛期持续、开始和结束的时间特征都不明显,并且分别对应着不同的周期 [21]。肖扬等用1961~2010年大渡河气象站点数据资料进行分析,得出:(1) 峨眉山是降水日数和降水量的高值区,但逐渐在减少,小金–丹巴是低值区。(2) 整个大渡河降水日数有4~8年的短周期 [22]。
前人分别研究了大渡河年径流量和降水量的关系、暴雨成因,极端降水指数分布特征,而对于大渡河流域降水的时空变化,目前进展为研究了上游汛期降水的时空分布特征、利用气象站资料研究整个流域降水的时空分布。与前人不同,本文是利用欧洲数值预报中心的ERA5再分析资料,对大渡河降水的时空变化特征进行研究。
1.3. 研究意义
青藏高原东南部到川西这一地带是大渡河的地理位置所在,河流横跨5个纬度、4个经度,位于99˚42'~103˚48'E,28˚15'~33˚33'N,是长江的二级支流,也是岷江的最大支流。整个流域有高山、有峡谷,存在多种地貌,地势、海拔差异巨大,因而沿流域一带的气候完全不同。长期以来,由于其特殊的地理位置和复杂的气候,导致泥石流、滑坡等自然灾害在流域沿岸频发,这些给国民经济、人民的生命财产等都造成了巨大的损失,而这些灾害一般都是由于降水过多所导致的。
目前对于大渡河降水时空分布的研究是不够全面的,还未有学者采用欧洲数值预报中心的数据对于大渡河降水时空分布进行更加系统的分析研究。本文恰希望通过研究,能够对大渡河流域降水空间分布特征、时间分布特征有更加深入的了解,揭示其气候变化的机理,可以为强降水预报预测提供技术支持,解决该地中长期气候变化预测。
2. 资料和方法
2.1. 研究区域概况
青藏高原东南部到川西这一地带是大渡河的地理位置所在。其上源为麻尔柯河、阿柯河(在久治县)经阿坝县于马尔康县境接纳梭磨河、绰斯甲河(杜柯河、多柯河,后称大金川),向南流经金川县、丹巴县,于丹巴县城东接纳小金川,再经泸定县、石棉县转向东流,经汉源县、峨边县,于乐山市城南注入岷江。流域总面积是7.77万平方公里,大渡河有比较多的支流,两条支流面积在1万平方公里以上,28条支流面积在1千平方公里以上,河网的密度较大。
大渡河流域上游是高原山地气候,雨水较少,年降水量在500到750毫米之间,夏季凉,冬季冷。其他地带是季风气候,冬季暖、夏季热,气候湿润、降水多,年降水量可以达到1000毫米,石棉右岸地区的降水量在1200到1500毫米之间,下游的某些地区甚至可以达到1400到1900毫米左右。暴雨发生在中下游地区的5月到9月,而其中7月、8月降水是最多的。大渡河水系是呈羽毛状延伸的,地表径流多来自于降水,融雪也提供了一部分。
2.2. 资料概况
由于大渡河流域的复杂地形,导致在该区域内的气象观测站点分布不均,从而在流域内的降水并不能完全通过常规意义上的原始站点观测到,因此需要精确率更高的一套数据集来展示大渡河流域的降水状况。目前国际上使用较多的格点数据包括ERA5和NCEP2再分析数据集,其中ERA5数据由ECMWF面向全球用户公开的再分析数据,是迄今为止最强大的全球气候监测数据集。
本文选择使用的数据是ERA5,也是最新的再分析资料。是由欧盟资助、欧洲中期数值预报中心(ECMWF)运营的气候服务中心开发,时间跨度是从1950年开始到如今,实时更新大约会有三个月左右的滞后。与其前身ERA-Interim相比,ERA5的性能有比较大的提升:(1) 0.125˚高时空分辨率:以水平空间分辨率31千米、高空每层0.1 hPa,共计137层(80千米)的空间分辨率,采集气象要素的小时数据(前身ERA-Interim空间分辨率为60层,每层0.1 hPa;时间分辨率为6小时)。(2) 新功能:第一次采用新型的集合型再分析产品来估计大气的不稳定度,该产品由10个成员构成,时间分辨率3小时,空间分辨率62千米,可以给在预报模式和实际观测当中所存在的各种误差提供一个较为合理的解释,也可以为不同时空的气象数据、大气参数的分析提供更加详细的资料和信息。(3) 更多的数据同化:将大量的历史卫星观测数据应用在更新型的模式和系统中,以便于估计与实际更为接近的大气状况,当然,这些全部的数据都会向所有的用户开发,供其下载和使用。(4) 更多的变量:提供了更多进行天气、气候、海洋分析等所需要的参数和变量,如今已经有多达240种(ERA-Interim只有100种),例如,海浪耦合的表征变量波高、波向。
综上,使用ERA5降水数据进行分析,无论是分辨率还是数据精确性方面都将得到极大提高,更能真实的反应出大渡河流域的降水特征,对该地区的水利、电力等方面的应用提供更好的参考。
2.3. 研究方法
2.3.1. 功率谱分析
功率谱是功率谱密度函数的简称,是单位频带内的信号功率,它表示了信号功率随着频率的变化情况,即信号功率在频域的分布状况 [23]。功率谱分析方法是分析时间序列常用的方法,它通过快速傅里叶变换研究频率与自相关函数的傅氏变换之间的关系,根据功率谱图的特点可以直观地揭示出序列的周期性。表达式为:
(1)
时间段内的功率信号。
为
的傅里叶变换。
2.3.2. 滤波
滤波是将信号波段中特定波段滤除的操作,是抑制和防止干扰的一项重要措施。是根据观察某一随机过程的结果,对另一与之有关的随机过程进行估计的概率理论与方法。滤波主要分为经典滤波和现代滤波两种。经典滤波是指任何一个满足一定条件的信号,都可以把它拆分成很多正弦波。现代滤波主要分为低通滤波、高通滤波、带通滤波。
在我们对一些气象要素进行分析的时候,经常需要剔除一些占比很大的、众所周知的主要周期,以此来突出其他周期的成分,因为他们的存在压制了其他的周期的表现。本文中我们采用了低通、带通滤波,即让过滤以后的成分只含有低频、固定频率的振动分量。
2.3.3. 经验正交函数(EOF分析)
EOF分析法是一种用于识别气候模式数据并突出其相似性和差异性的普遍方法。它是一种标准的统计方法,经常用于气象研究中,将原始的相关变量减少到小部分新的不相关的变量值中,这些变量可以解释大部分的方差,这种方法在气候数值模拟中有着广泛的应用 [24]。
2.3.4. Mann-Kendall检验法
气候的突变是相对稳定的不连续跳跃,即是指气候从一种状态跳跃性的向另一种状态转变的现象。世界气象组织(WMO)倡议,使用Mann-Kendall test法来评估气候学和水文学的趋势,这是时间序列的分析方法之一,这种检验被称为Kendall’tau统计,是一种非参数检验,即:不要求样本遵从一定的分布,不受到异常值的干扰,适用于非正态分布的数据 [25]。本文主要使用Mann-Kendall突变检验方法,通过对所需要的正反序列进行特定标准化处理以后,得到两条曲线在置信区间的交点,从而确定出突变点。
2.3.5. 小波分析法
傅里叶变换对随时间稳定变化的波动(信号)的处理,是非常有效的,目前应用仍旧广泛。但是对于波动不稳定信号处理结果是不太理想的。而小波分析是处理不稳定信号的重要工具,通过对时间(空间)和频率进行局部变换,利用伸缩、平移等运算进行多尺度的细化分析,以从不稳定的信号中提取出来有用的信息 [26]。
小波分析这种时间序列分析方法,目前在各个领域的应用都很广泛,尤其在对气象要素进行时间分析时。本文利用小波分析方法,对年降水量进行处理,得到年降水量随时间变化的各种尺度,分析序列中所包含的周期特征 [22]。
3. 研究结果
3.1. 大渡河流域降水的空间特征分析
3.1.1. 降水量月平均、季平均、年平均空间分布特征
降水平均值可以表征某地降水量的多少,降水方差可以表征某地降水均匀程度,本文通过对大渡河流域降水量的均值、方差进行月、季、年尺度上的分析,来研究其整个流域降水的空间分布特征。
图1是大渡河流域1979~2018年月平均降水量。从图中可以得出,大渡河流域月平均降水量数值大致位于100~700 mm之间,其中1月、2月、3月、11月、12月的降水较少,基本都在200 mm以下;5月、6月、7月、8月、9月降水多,基本都在400 mm以上,其中尤以6月、7月、8月降水最多,整个流域都在450 mm以上;而4月、10月降水量在200~300 mm之间。对于整个大渡河流域而言,上游月降水量最少,下游次之,中游雅安地区(石棉到汉源一带)最多,其月降水量在7月、8月达到最大,有将近700 mm,即使是在10月、4月这样降水少的季节,也有将近400 mm,而整个流域降水最少的地方是在北纬31˚,东经102˚ (丹巴)处,即使在8月、9月,其月降水量也仅有250 mm左右。
图2是大渡河流域1979~2018年季平均降水量,图2(a)、图2(b)、图2(c)、图2(d)分别是第一、二、三、四季度。从图中可以得出,大渡河流域季平均降水量数值大致位于600~1600 mm之间,其中第四季度的平均降水最少,大约只有600 mm;第三季度降水次少,基本在600~1000 mm之间,第一季度降水较多,大致在800~1200 mm之间,而第二季度的平均降水量是最多的,在1400~1800 mm之间,这与实际情况基本一致。第二季度正处于汛期,降水量恰是一年之中最多的。整个大渡河流域降水的空间分布特征与月平均降水量表征的情况一致,也是上游降水量最少,下游次之,中游雅安地区(石棉到汉源一带)最多,其降水量在第二季度达到最大,有1800 mm,即使是在第三季度,也有将近1000 mm;而整个流域降水最少的地方是在北纬31˚,东经102˚ (丹巴)处,即使在第二季度,其平均降水量也仅有1000 mm左右。
图3是大渡河流域1979~2018年年平均降水量。从图中可以得出,大渡河流域年平均降水量数值大致在2000~4500 mm之间。整个大渡河流域降水的空间分布特征与月平均降水量、季平均降水量表征的情况一致,也是上游降水量最少,下游次之,中游雅安地区(石棉到汉源一带)最多。中游年平均降水量中心值有4500 mm,从中心向外逐渐减少,形成了一个降水中心,最外侧为大渡河流域边界,年平均降水量为3000 mm。在大渡河流域下游,降水量数值都为3000 mm。整个流域降水最少的地方是在北纬31˚,东经102˚ (丹巴)处,其年平均降水量仅有2000 mm左右。
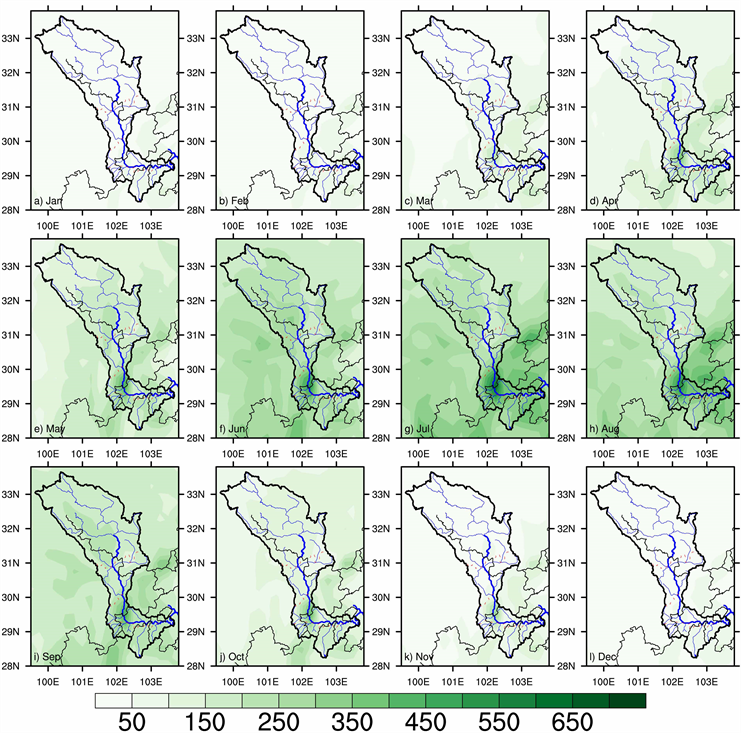
Figure 1. Monthly average precipitation of Dadu River Basin (inside the thick black solid line in the figure) from 1979 to 2018
图1. 大渡河流域(图中粗黑色实线内部) 1979~2018年月平均降水量
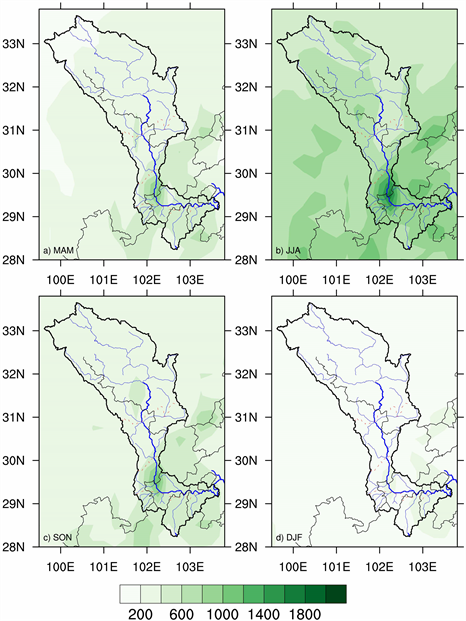
Figure 2. Seasonal average precipitation in Dadu River Basin from 1979 to 2018
图2. 大渡河流域1979~2018年季平均降水量
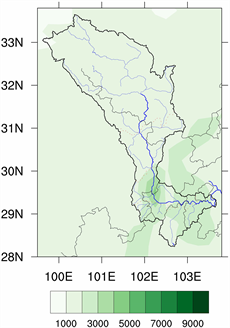
Figure 3. Annual average precipitation of Dadu River Basin from 1979 to 2018
图3. 大渡河流域1979~2018年年平均降水量
3.1.2. 降水量月方差、季方差、年方差空间分布特征
图4是大渡河流域降水量1979~2018年月平均方差。从图中可以得出,10月、11月、12月三个月的月平均方差数值是最小的,在0.5以下,而且这三个月整个大渡河流域的月平均方差不存在空间变化,结合图1中月平均降水量的数值,我们可以得到:10月、11月、12月这三个月降水少而且均匀,整个流域降水量数值差异不大。1月、2月、3月、4月、5月、9月整体特征表现与10月、11月、12月一致,唯一的区别是方差值稍大一些,大概有0.5左右。6月在大渡河下游为一个方差大值小区域,数值达到了1,结合图1中6月此地降水数值为400 mm,说明:此地区6月份降水量适中,但降水不均匀集中。7月、8月方差大值区域相同,在北纬103˚~104˚,东经30˚~31˚ (石棉–雅安)这个小区域内,7月中心数值为2,8月为2.5,结合图1,此地也是降水量的小中心,说明:在7、8月份此地降水量大但降水不均匀集中。
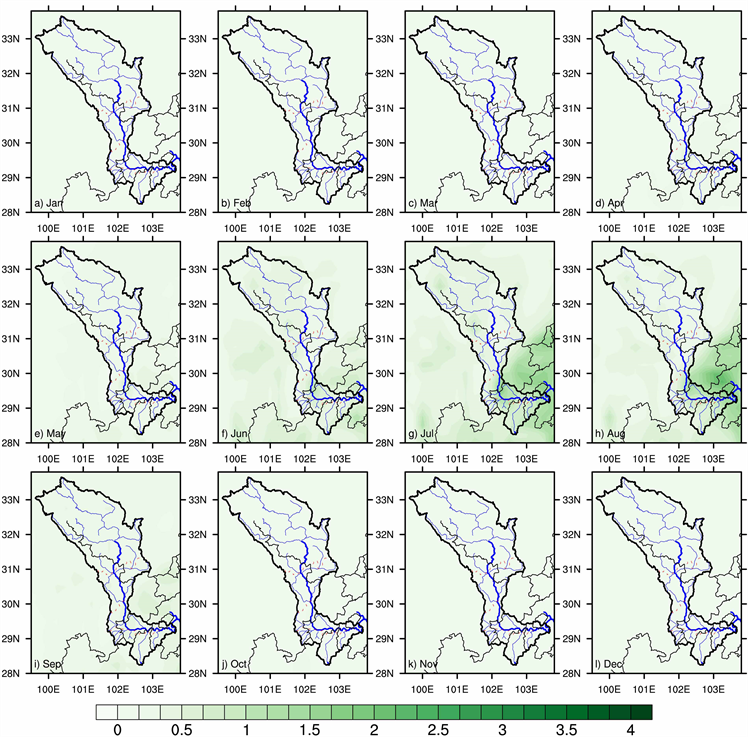
Figure 4. Monthly mean variance of precipitation in Dadu River Basin from 1979 to 2018
图4. 大渡河流域降水量1979~2018年月平均方差
图5是大渡河流域降水量1979~2018年季平均方差。从图中可以得出,第一季度和第四季度的季平均方差数值是最小的,在0.5以下,而且两个季度整个大渡河流域的月平均方差不存在空间变化,结合图2中季平均降水量的数值,我们可以得到:第一季度和第四季度降水少而且均匀,整个大渡河流域降水量数值差异不大。第三季度有一个方差大值的带状区域和一个大值中心,该带状区域从北纬31˚,东经103.5˚向下到大渡河流域中游拐角处,中心数值为而1.25,而大值中心与该带状区域相连,在拐角处上方,中心数值为1。结合图2中第三季度降水数值,说明:此地降水较少而且不均匀集中。第二季度的季平均方差是最大的,在整个大渡河流域中游(雅安)有一片方差大值区域,其中有两个大值中心和一个小值中心,两个大值中心数值超过1.5,而小值中心数值为0.75。同时石棉一带仍旧有一中心数值为1的方差区域,而下游下方有一中心数值与上方两个大值中心不相上下的方差大值区域。这些大值、小值区域基本上都呈现菱形、三角形而非圆形。

Figure 5. Seasonal mean variance of precipitation in Dadu River Basin from 1979 to 2018
图5. 大渡河流域降水量1979~2018年季平均方差
图6是大渡河流域降水量1979~2018年年平均方差。从图中可以得出,在整个大渡河流域中游(雅安)有一片方差大值区域,中心数值为0.75。同时拐角处仍旧有一中心数值为0.75的方差区域,而下游下方有一中心数值为0.625方差大值区域。这些大值、小值区域基本上都呈现菱形、三角形而非圆形。结合图3年平均降水量数值,我们发现:大渡河上游年平均降水数值小,方差小,即上游降水少而降水均匀集中;中游雅安地区(石棉到汉源一带),年平均降水数值大,方差大,即中游降水多而不均匀集中;下游年平均降水数值适中,方差小,即下游降水适中而且降水均匀集中。
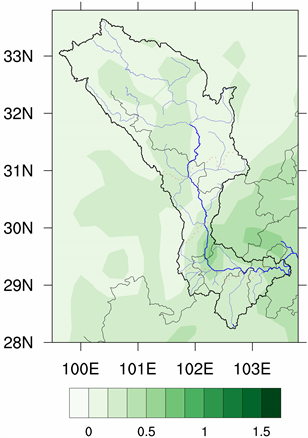
Figure 6. Annual mean variance of precipitation in Dadu River Basin from 1979 to 2018
图6. 大渡河流域降水量1979~2018年年平均方差
3.1.3. 降水量月降水变率、季降水变率、年降水变率空间分布特征
降水平均值可以表征某地降水量的多少,降水方差可以表征某地降水均匀程度,降水变率是表征降水量变动程度的物理量。本文中采用方差除以平均值,来表征降水变量,分析多年来大渡河流域降水量的变化特征。
图7是大渡河流域1979~2018年平均月降水变率。从图中可以得出,在整个大渡河流域,多年月平均降水变率,在各个月份差距并不大,但是在大渡河流域中游的石棉到雅安这一带地区,月平均降水变率都要高于其他地区,尤其7~8月,该地区数值在0.0012以上,特别的,在8月这个地区有一个中心数值为0.002的高值中心和一个中心数值为0.0014的次高值中心。10月、11月、12月、1月、2月的降水变率很小,只有0.0002,结合图1中,月平均降水量数值,我们可以得出与图4中较为一致的结论,即1月、2月、10~11月降水量少但降水较为均匀、变动小。3月、4月的月平均降水变率的数值为0.01,上游、下游数值都高于中游地区,这说明在3月、4月整个大渡河降水量少而且降水不均匀集中。5月、9月整体上,大渡河流域月降水变率为0.006,5月在大渡河下游末端有一降水变率的高值中心,达到了0.01,而9月在雅安也存在一个中心值为0.0014的高值中心。6月的中心值为0.0018的高值中心是在大渡河流域末端南部甘洛县一带。
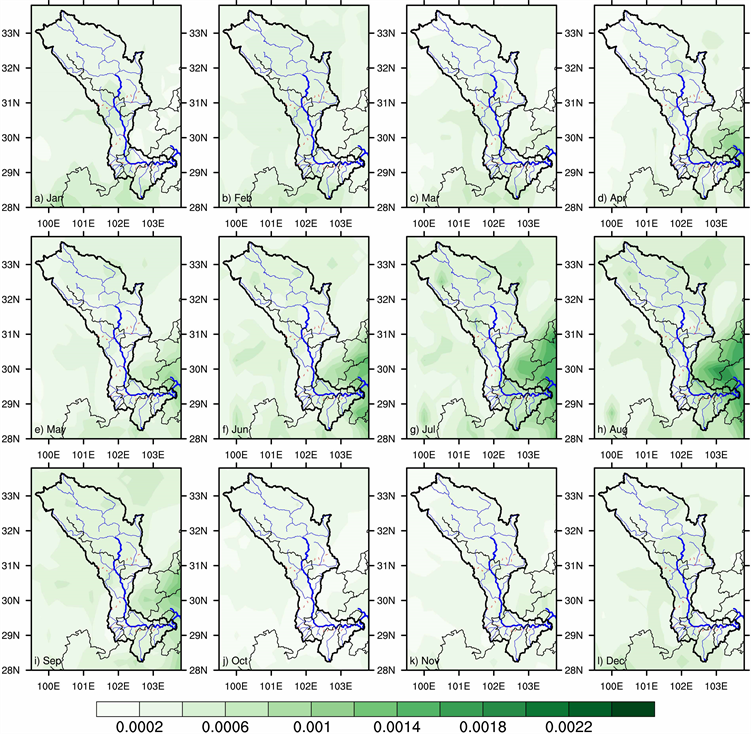
Figure 7. Monthly average precipitation variability of Dadu River Basin from 1979 to 2018
图7. 大渡河流域1979~2018年月平均降水变率
图8是大渡河流域1979~2018年季平均降水变率。从图中可以得出,在整个大渡河流域,多年季平均降水变率,在各个季度的特征不同。在第一季度,整个大渡河流域降水变率数值均匀且较小,为0.0005。结合图2中第一季度的降水量小,可以得出第一季度大渡河流域降水量少、降水均匀、降水变动程度小。这与图5中季平均方差的结论是一致的。第四季度整体降水变率数值在0.0005以上,同时在大渡河上游、中游分别有两个高值中心,上游为0.0006,中游可达到0.0007。这说明:第四季度大渡河流域各个地区降水集中程度是有差异的,这与图5中结论有所不同。第二季度在雅安地区、大渡河流域下游南部的甘洛县一带有中心值为0.0009的高值中心,并且在雅安地区这个高值中心的范围较大,说明此地降水很大且不均匀集中、降水变动程度大。同样地,第三季度在雅安地区也有一范围较大的高值中心,中心数值甚至达到了0.001以上,结合图2中该地降水数据,不难得出:该地降水较大且不均匀集中。
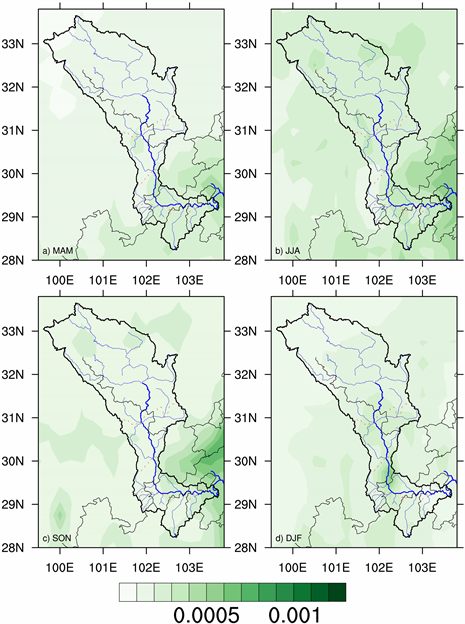
Figure 8. Seasonal average precipitation variability in Dadu River Basin from 1979 to 2018
图8. 大渡河流域1979~2018年季平均降水变率
图9是大渡河流域1979~2018年年平均降水变率。从图中可以得出,在整个大渡河流域年降水变率的差异并不大,上游中游稍大一些,在中游石棉到雅安地区有一片年降水变率大值区域,中心数值达到为0.0004,在下游南部也有一中心数值0.00024的次极值中心,这两个大值区域呈现菱形、三角形而非圆形。结合图3、图6,我们发现:大渡河上游年平均降水数值小,年平均降水变率小,年方差小,即上游降水少而降水均匀集中、变动程度小;中游雅安地区(石棉到汉源一带),年平均降水数值大,年平均降水变率大,年平均方差大,即下游降水多而不均匀集中、变动程度大;中游年平均降水数值适中,方差小,年平均降水率小,即中游降水适中而且降水均匀集中。
3.2. 大渡河流域降水的时间特征分析
3.2.1. 29.5˚N,102.25˚E处日降水变化
选取大渡河流域降水最多的地点,即29.5˚N,102.25˚E,石棉处,研究其一天之内降水量的变化,分析一天之内哪些时刻降水量更多一点。
图10是29.5˚N,102.25˚E处小时降水量的变化。从图中可以看出,小时降水量的数值在0.66~0.93 mm之间,从0点至5点,小时降水量一直在减少,5点达到一天中小时降水最小值0.66 mm,从5点至19点,小时降水整体上呈现增加趋势,分别在8点、16点、19点达到三个极大值点0.85 mm、0.86 mm、0.93 mm,且极大值对应数值也是递增的趋势。相应地,在10点和18点有两个极小值分别是0.77 mm和0.81 mm;从19点往后,小时降水量又呈现减少趋势。特别地,5点到6点、9点到10点,这两个小时内降水稳定,降水量几乎不变;而6点到7点,18点到19点,这两个小时内,降水都存在一个峭壁式的增加,从极小值直接增长至极大值。
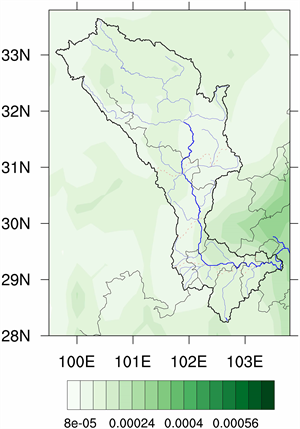
Figure 9. Annual average precipitation variability of Dadu River Basin from 1979 to 2018
图9. 大渡河流域1979~2018年年平均降水变率
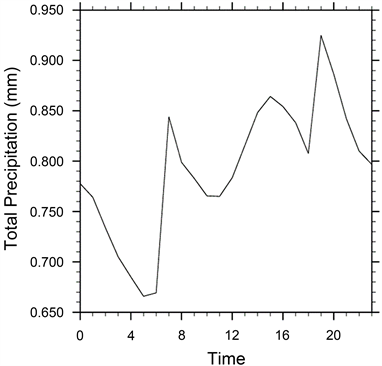
Figure 10. Variation of hourly precipitation at 29.5˚N, 102.25˚E
图10. 29.5˚N,102.25˚E处小时降水量的变化
3.2.2. 降水长期变化趋势
通过对月降水量进行区域平均后线性拟合,求得时间序列,得到大渡河流域降水长期变化趋势。
图11是对大渡河流域区域平均以后的月降水量数据进行线性拟合所得到的,经过了置信水平0.05的检验。从图中可以看出,大渡河流域降水量整体而言,呈现下降趋势,由回归系数可以得出,大渡河流域降水减少幅度为−0.087/a。
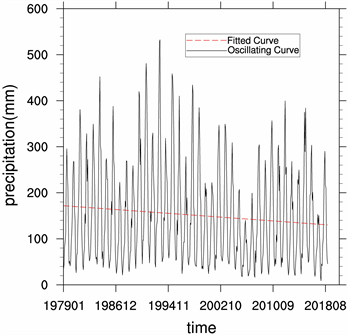
Figure 11. Linear fitting of monthly precipitation from 1979 to 2018
图11. 1979~2018年月降水量的线性拟合
3.2.3. 降水的主要变化周期和演变规律
对月尺度的降水量进行功率谱分析,以此获得波动的主周期。如由月尺度降水量功率谱图(图12)可知,在置信区间内,频率0.021时所对应的方差最大且远大于其他功率对应的方差,因此月尺度降水量的波动具有明显的主频率即0.021,对应的周期为47.6个月。

Figure 12. Power spectrum of monthly precipitation
图12. 月尺度降水量的功率谱
根据图12中功率谱获得的主周期47.6个月,对月降水量距平数据进行48个月的低通滤波(图13),发现:低通滤波后,其振动周期没有明显的规律性,振幅也不大,不超过0.5,但是整体上呈现下降趋势。特别地,1987年12月、2006年12月位于波谷,代表该月为降水低值月,其中2006年12月的振幅达到了最大值0.5。

Figure 13. Low pass filtering with a monthly scale of 48 months
图13. 月尺度为48个月的低通滤波
根据功率谱获得的主周期来对月尺度降水量距平序列进行47~48个月的带通滤波(图14),整个波动的振幅较小,距平值不超过1.2 × 10−10。其中,1980年1月、1984年1月,1987年1月为波谷,对应极小值是降水量的低值月,1983年8月、1985年8月、1989年8月为波峰,对应极大值是降水量的高值月。
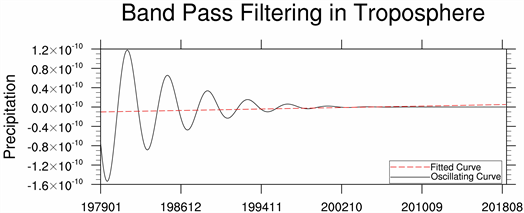
Figure 14. Band pass filtering of 47 - 48 months monthly precipitation
图14. 月降水量47~48个月的带通滤波
对 ~2018年年降水量数值进行小波分析(图15)以后,并未发现有存在明显的周期变化。
3.2.4. 气候突变年份
为了研究 ~2018年,大渡河流域降水量是否稳定,或是否发生突变,本文使用Mann-Kendall检验法和滑动t检验法对大渡河流域月降水量进行非线性检验,结果如下:
月降水量的突变特征为:(图16)整体而言,月降水量呈现减少的趋势。
20世纪以前,UF曲线基本在0刻度线以上,整体月降水量趋势是增加的,但是增加的程度是有差异的,而其中1986~1990年却是在0刻度线以下,即呈现减少的趋势。20世纪以后,UF曲线完全在0刻度线以下,说明20世纪以来,大渡河流域月降水量一直在减少,且随着时间推移,减少的程度是越来越剧烈。UF曲线和UB曲线在0.05的水平置信区间只有一个交点,通过滑动t检验,可以确定突变发生在2002年。
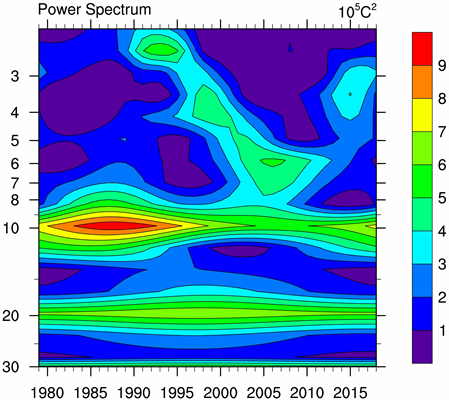
Figure 15. Wavelet analysis of annual precipitation from 1979 to 2018
图15. 1979~2018年年降水量的小波分析
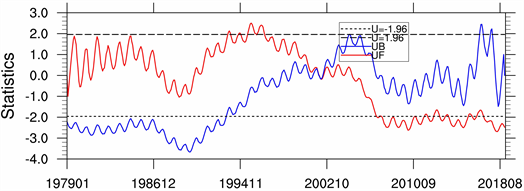
Figure 16. M-K mutation test from 1979 to 2018
图16. 1979~2018年的M-K突变检验
4. 结论与展望
4.1. 主要结论
经过对大渡河流域降水量的研究,我们得出以下几个结论:
(1) 月平均降水量7、8月最多,12月最少;季平均降水量第二季度最多,第四季度最少;年平均降水量最少的为2000 mm,最多的地带可以达到4500 mm。
(2) 上游降水最少,但降水均匀集中;下游降水适中,在第二第三季度降水变动较大;中游雅安地区(石棉到汉源一带)一直是降水最多的地带。
(3) 石棉一带小时降水量:从5点到19点,降水量整体呈现增加趋势,19点是一天之内降水最多的时刻,为0.93 mm,5点是一天之内降水最少的时刻,仅0.66 mm。从19点到次日5点,降水量是一直在减少。
(4) 主周期47.6个月,低通滤波发现降水量的整体趋势是在减少,波动的振幅较小且不规律,波动周期也呈现不规律特征;带通滤波发现虽整体趋势是有很小程度的增加,整个波动的振幅很小,且随时间逐渐减小,2002年以后波动基本消失。
(5) M-K检验发现大渡河流域降水突变发生在2002年,此前降水基本上都是呈现增加趋势,但增加幅度不稳定,此后降水一直在减少,而且减少的幅度在增大。
4.2. 存在的问题与展望
本文的研究还有许多不足之处,主要有如下问题:
首先,由于时间有限,针对于大渡河流域的时空分布特征的研究做的还不够深入,只从均值、方差、降水变率研究其空间分布特征,时间分布特征只研究了其周期变化,今后需要做更多更深入的分析。
其次,再分析数据虽然分辨率高,但是降水反演精度较低,对于研究结果有一定影响,往后应该结合精度较高的站点数据,进一步完善本文。
最后,由于受气候变化和人类活动的双重影响,大渡河流域降水序列在某种意义上易发生变化,其统计特性随着时间的推移也会发生变化,未来仍有深入研究的必要。
致谢
本文是在我大学期间的科研导师——蔡宏珂老师的指导下完成的,在此我真诚感谢他对我的指导和帮助。