广义Fornberg-Whitham方程的某些非线性波解

Some Nonlinear Wave Solutions for the Generalized Fornberg-Whitham Equation

摘要: 本文利用微分方程定性理论和动力系统分支方法寻找广义Fornberg-Whitham方程的非线性波解，当次数n = 2时，我们获得了四个非线性波解；当次数n = 3时，我们获得了一个非线性波解。

Abstract: In this paper, the qualitative theory of differential equations and the bifurcation method of dynamical systems are used to find nonlinear wave solutions of the generalized Fornberg-Whitham equation. When n = 2, we obtained four nonlinear wave solutions. When n = 3, we obtained one nonlinear wave solution.

1. 引言

本文利用微分方程定性理论和动力系统的分支方法 [1] [2] [3] [4] 研究n阶并带有参数b的广义Fornberg-Whitham (F-W)方程

$u_t-u_{xxt}+b{u}_x+u^n{u}_x=3u_x{u}_{xx}+u{u}_{xxx}.$ (1)

方程(1)是F-W方程 [5] [6] 的广义形式，F-W方程具有如下形式

$u_t-u_{xxt}+u_x+u{u}_x=3u_x{u}_{xx}+u{u}_{xxx}.$ (2)

Fornberg和Whitham给出了方程(2)的一个尖孤立波解 $u\left(x,t\right)=A{\text{e}}^{-\frac{1}{2}\left|x-\frac{4}{3}t\right|}$，其中A为任意常数 [7]。由于F-W方程不具有像Camassa-Holm (C-H)方程 [8]

$u_t-u_{xxt}+3u{u}_x=\text{2}{u}_x{u}_{xx}+u{u}_{xxx}$ (3)

这样完全可积和双Hamilton结构 [8] 等良好性质，一直并未引起广泛研究。直到近年来，F-W方程重新引起了大家的关注。

当b = 1，n = 2时，He和Meng等人给出了方程(1)的尖孤立波解 [9]，Liang给出了精确的行波解 [10]。此外，Yang和Fan将F-W方程推广成二元F-W方程

$\{\begin{array}{l}{u}_t=u_{xxt}-u_x-u{u}_x+3u_x{u}_{xx}+u{u}_{xxx}+{\rho }_x\\ {\rho }_x=-{\left(\rho u\right)}_x\end{array}$ (4)

并得到方程的光滑周期波、光滑孤立波和扭波等波解 [11]。Bi和Jiang研究了带线性色散项的F-W方程

$u_t-u_{xxt}+u_x+u{u}_x=3u_x{u}_{xx}+u{u}_{xxx}-u_{xxx}$ (5)

证明了光滑和非光滑行波解的存在性，并给出了显示孤立波解 [12]。

本文主要研究当n = 2, 3时，方程(1)的某些非线性波解。

2. 主要结果

当n = 2时，令

$c_0=4\left(2+\sqrt{4-b}\right)$ (6)

$c_1=\frac{1}{2}\left(1+\sqrt{1-4b}\right)$ (7)

$c_2=\frac{1}{2}\left(1-\sqrt{1-4b}\right)$ (8)

$k=\frac{\sqrt{15}}{12}\sqrt{16c-c^2-16b}$ (9)

$w_1=\sqrt{\frac{5}{4}c+2k}+\sqrt{3k}$ (10)

$w_2=\sqrt{\frac{5}{4}c+2k}-\sqrt{3k}$ (11)

$u_1\left(x,t\right)=3k{\tanh }^{-\text{2}}\left(\sqrt{\frac{k}{10}}\left(x-ct\right)\right)-\frac{1}{4}c-2k$ (12)

$u_2\left(x,t\right)=3k{\left(\frac{w_1{\text{e}}^{\sqrt{\frac{2k}{5}}\left|x-ct\right|}+w_2}{w_1{\text{e}}^{\sqrt{\frac{2k}{5}}\left|x-ct\right|}-w_2}\right)}^2-\frac{1}{4}c-2k$ (13)

$u_3\left(x,t\right)=3k{\tanh }^{\text{2}}\left(\sqrt{\frac{k}{10}}\left(x-ct\right)\right)-\frac{1}{4}c-2k$ (14)

$u_4\left(x,t\right)=\frac{1}{{\left(\frac{1}{\sqrt{30}}\left|x-c_{0}t\right|+\frac{2}{\sqrt{5c_0}}\right)}^2}-\frac{1}{4}{c}_0$ (15)

1) 当 $b\le 0$，且 $0<c<c_0,c\ne c_1$ 时， $u_1\left(x,t\right)$， $u_2\left(x,t\right)$， $u_3\left(x,t\right)$， $u_4\left(x,t\right)$ 是方程(1)的解；

2) 当 $0<b<\frac{1}{4}$，且 $b<c<c_0,c\ne c_1,c\ne c_2$ 时， $u_1\left(x,t\right)$， $u_2\left(x,t\right)$， $u_3\left(x,t\right)$， $u_4\left(x,t\right)$ 是方程(1)的解；

3) 当 $b=\frac{1}{4}$，且 $b<c<c_0,c\ne c_1$ 时， $u_1\left(x,t\right)$， $u_2\left(x,t\right)$， $u_3\left(x,t\right)$， $u_4\left(x,t\right)$ 是方程(1)的解；

4) 当 $\frac{1}{4}<b$，且 $b<c<c_0$ 时， $u_1\left(x,t\right)$， $u_2\left(x,t\right)$， $u_3\left(x,t\right)$， $u_4\left(x,t\right)$ 是方程(1)的解。

当n = 3时，令

$\delta =\sinh \left(\alpha +arsinh\left(\beta \right)\right)$ (16)

$\alpha =\frac{\left|x-ct\right|}{\sqrt{12}}\sqrt{f+e\gamma +{\gamma }^2}$ (17)

$\beta =\frac{2\left(f+\gamma c\right)+e\left(c+\gamma \right)}{\left(c-\gamma \right)\sqrt{4f-e^2}}$ (18)

$f=\frac{12c\rho +\frac{6}{15}{\gamma }^2{c}^2+c^2{\gamma }^3}{c\left(\gamma c+{\gamma }^2\right)}$ (19)

$\gamma =-\frac{c}{5}-\frac{9}{5}{l}^{\frac{1}{3}}{c}^2+\frac{1}{30}{\left(\frac{1}{l}\right)}^{\frac{1}{3}}$ (20)

$p=-54000b+54000c-1512c^3$ (21)

$q=\sqrt{62985\text{6}{c}^6+p^2}$ (22)

$e=\frac{4}{5}c+2\gamma$ (23)

$l=\frac{2}{p+q}$ (24)

$\begin{array}{l}\rho =\frac{1}{40}(-12bc+12c^2-\frac{63}{125}{c}^4-\frac{q}{13500}c+\frac{2916}{125}l{c}^7-\frac{243}{125}{l}^{\frac{2}{3}}{c}^6+36b{l}^{\frac{1}{3}}{c}^3\\ +\frac{126}{125}{l}^{\frac{1}{3}}{c}^5+\frac{2}{3}\left(c-b\right)l^{\frac{1}{3}}-\frac{7}{375}{\left(\frac{1}{l}\right)}^{\frac{1}{3}}{c}^3-\frac{1}{1500}{\left(\frac{1}{l}\right)}^{\frac{2}{3}}{c}^2)\end{array}$ (25)

$u_5\left(x,t\right)=\frac{\gamma \delta \sqrt{4f-e^2}+2f+e\gamma }{\delta \sqrt{4f-e^2}-2\gamma -e}$ (26)

$c_3^1$， $c_3^{\text{2}}$ 由方程(27)决定

$\frac{\text{3}}{\text{4}}{\left(c-b\right)}^{\frac{\text{4}}{\text{3}}}=-\frac{1}{\text{4}}{c}^{\text{4}}+c^2-bc$ (27)

1) 当 $b\le 0$，且 $0<c<+\infty ,c\ne c_{\text{3}}^{\text{2}}$ 时， $u_5\left(x,t\right)$ 是方程(1)的解；

2) 当 $0<b<\frac{\text{2}}{\text{3}\sqrt{\text{3}}}$，且 $\text{0}<c<+\infty ,c\ne c_{\text{3}}^{\text{1}},c\ne c_{\text{3}}^{\text{2}}$ 时， $u_5\left(x,t\right)$ 是方程(1)的解；

3) 当 $b=\frac{\text{2}}{\text{3}\sqrt{\text{3}}}$，且 $\text{0}<c<+\infty ,c\ne c_{\text{3}}^{\text{1}}$ 时， $u_5\left(x,t\right)$ 是方程(1)的解；

4) 当 $\frac{\text{2}}{\text{3}\sqrt{\text{3}}}<b$，且 $\text{0}<c<+\infty$ 时， $u_5\left(x,t\right)$ 是方程(1)的解。

此外，我们已通过如下的Mathematica程序验证了由式子(12)，(13)，(14)，(15)，(26)分别给出的解 $u_1\left(x,t\right)$， $u_2\left(x,t\right)$， $u_3\left(x,t\right)$， $u_4\left(x,t\right)$， $u_5\left(x,t\right)$ 的正确性

$\begin{array}{l}D\left[u,t\right]-D\left[u,x,x,t\right]+bD\left[u,x\right]+u^{n}D\left[u,x\right]\\ -3D\left[u,x\right]D\left[u,x,x\right]-uD\left[u,x,x,x\right].\end{array}$

具体推导如下。

3. 行波系统及首次积分

首先，对方程(1)做行波变换

$u\left(x,t\right)=\phi \left(\xi \right),\xi =x-ct$ (28)

其中 $c>0$ 为常波速。

得到常微分方程

$3{\phi }^{\prime }{\phi }^{″}+\phi {\phi }^{‴}+c{\phi }^{\prime }-c{\phi }^{‴}-b{\phi }^{\prime }-{\phi }^n{\phi }^{\prime }=0$ (29)

再将方程(29)进行积分一次，得到

$\left(c-b\right)\phi +{\left[{\phi }^{\prime }\right]}^2+\left(\phi -c\right){\phi }^{″}-\frac{1}{n+1}{\phi }^{n+1}=g$ (30)

其中，g为积分常数。

令

$\frac{\text{d}\phi }{\text{d}\xi }=y$ (31)

将(31)带入方程(30)，得到平面系统

$\{\begin{array}{l}\frac{\text{d}\phi }{\text{d}\xi }=y\\ \frac{\text{d}y}{\text{d}\xi }=\frac{g+\left(b-c\right)\phi +\frac{1}{n+1}{\phi }^{n+1}-y^2}{\phi -c}\end{array}$ (32)

令

$\frac{\text{d}\xi }{\phi -c}=\text{d}\tau$ (33)

将系统(32)转换为

$\{\begin{array}{l}\frac{\text{d}\phi }{\text{d}\tau }=\left(\phi -c\right)y\\ \frac{\text{d}y}{\text{d}\tau }=g+\left(b-c\right)\phi +\frac{1}{n+1}{\phi }^{n+1}-y^2\end{array}$ (34)

由于系统(32)和系统(34)有相同的首次积分(35)

${\left(\phi -c\right)}^2{y}^2-\left(\frac{2}{\left(n+3\right)\left(n+1\right)}{\phi }^{n+3}-\frac{2c}{\left(n+2\right)\left(n+1\right)}{\phi }^{n+2}+\frac{2}{3}\left(b-c\right){\phi }^3+\left(g+c\left(c-b\right)\right){\phi }^2-2gc\phi \right)=h$ (35)

所以两个系统除了奇直线 $\phi =c$ 之外有相同的拓扑相图。因此我们可以通过研究系统(34)的相图达到研究系统(32)的相图的目的。

令

$\begin{array}{c}{H}_n\left(\phi ,y\right)={\left(\phi -c\right)}^2{y}^2-(\frac{2}{\left(n+3\right)\left(n+1\right)}{\phi }^{n+3}-\frac{2c}{\left(n+2\right)\left(n+1\right)}{\phi }^{n+2}\\ +\frac{2}{3}\left(b-c\right){\phi }^3+\left(g+c\left(c-b\right)\right){\phi }^2-2gc\phi )\end{array}$ (36)

则有

$h=H_n\left(\phi ,y\right)$ (37)

4. 分支曲线

令

$f\left(\phi \right)=g+\left(b-c\right)\phi +\frac{1}{n+1}{\phi }^{n+1}$ (38)

$f_0\left(\phi \right)=\left(b-c\right)\phi +\frac{1}{n+1}{\phi }^{n+1}$ (39)

则

$f\left(\phi \right)=g+f_0\left(\phi \right)$ (40)

系统(34)变为

$\{\begin{array}{l}\frac{\text{d}\phi }{\text{d}\tau }=\left(\phi -c\right)y\\ \frac{\text{d}y}{\text{d}\tau }=f\left(\phi \right)-y^2\end{array}$ (41)

显然，系统(41)的奇点都在 $\phi$ 轴或直线 $\phi =c$ 上。由(40)可得

${f^{\prime }}_0\left(\phi \right)=\left(b-c\right)+{\phi }^n$ (42)

当 $n=2m+1$ 时， ${f^{\prime }}_0\left(\phi \right)$ 有一个零点

${\phi }_n^0={\left(c-b\right)}^{\frac{1}{n}}$ (43)

为 $f\left(\phi \right)$ 的极小值点。

当 $n=2m$ 时， ${f^{\prime }}_0\left(\phi \right)$ 有两个零点 $\pm {\phi }_n^0$，其中 $-{\phi }_n^0$ 为 $f\left(\phi \right)$ 的极大值点， ${\phi }_n^0$ 为 $f\left(\phi \right)$ 的极小值点。

令

$g_n^a\left(c\right)=-f_0\left({\phi }_n^0\right)=\frac{n}{n+1}{\left(c-b\right)}^{\frac{n+1}{n}}$ (44)

$g_n^b\left(c\right)=-f_0\left(c\right)=\left(c-b\right)c-\frac{1}{n+1}{c}^{n+1}$ (45)

再定义 $g=g_n^d\left(c\right)$ 分支曲线，满足在这条分支曲线上有三个鞍点相连。曲线表达式可由下面方程组解出

$\{\begin{array}{l}{H}_n\left(\phi ,0\right)=H_n\left(c,\sqrt{f\left(c\right)}\right)\\ f\left(\phi \right)=0\end{array}$ (46)

接下来研究在c-g平面上，系统(41)的分支相图。

5. 当n = 2时的分支相图

$c_3=2\left(1+\sqrt{1-b}\right)$ (47)

$c_4=2\left(1-\sqrt{1-b}\right)$ (48)

$g_2^a\left(c\right)=\frac{2}{3}{\left(c-b\right)}^{\frac{3}{2}}$ (49)

$g_2^b\left(c\right)=-\frac{1}{3}{c}^3+c^2-cb$ (50)

$\begin{array}{l}{g}_2^d\left(c\right)=-\frac{1}{6}bc+\frac{1}{6}{c}^2-\frac{1}{48}{c}^3\\ +\frac{\sqrt{15}}{432}\sqrt{16c-16b-c^2}\left(16c-16b-c^2\right)\end{array}$ (51)

$c_0$ 由式子(6)给出， $c_1$ 由式子(7)给出， $c_2$ 由式子(8)给出。具体情况如下：

1) 当 $b<0$ 时， $g_{\text{2}}^a\left(c\right)$， $g_{\text{2}}^b\left(c\right)$， $g_{\text{2}}^d\left(c\right)$ 三支曲线交于 $c_1$， $-g_{\text{2}}^a\left(c\right)$ 与 $g_{\text{2}}^b\left(c\right)$ 交于 $c_3$， $-g_{\text{2}}^a\left(c\right)$ 与 $g_{\text{2}}^d\left(c\right)$ 交于 $c_0$。

2) 当 $b=0$ 时， $g_{\text{2}}^a\left(c\right)$， $g_{\text{2}}^b\left(c\right)$， $g_{\text{2}}^d\left(c\right)$ 三支曲线交于 $c_{\text{1}}$， $-g_{\text{2}}^a\left(c\right)$ 与 $g_{\text{2}}^b\left(c\right)$ 交于 $c_3$， $-g_{\text{2}}^a\left(c\right)$ 与 $g_{\text{2}}^d\left(c\right)$ 交于 $c_0$。

3) 当 $0<b<\frac{1}{4}$ 时， $g_{\text{2}}^a\left(c\right)$， $g_{\text{2}}^b\left(c\right)$， $g_{\text{2}}^d\left(c\right)$ 三支曲线交于 $c_{\text{1}}$， $c_{\text{2}}$， $-g_{\text{2}}^a\left(c\right)$ 与 $g_{\text{2}}^b\left(c\right)$ 交于 $c_3$， $-g_{\text{2}}^a\left(c\right)$ 与 $g_{\text{2}}^d\left(c\right)$ 交于 $c_0$。

4) 当 $b=\frac{\text{1}}{\text{4}}$ 时， $g_{\text{2}}^a\left(c\right)$， $g_{\text{2}}^b\left(c\right)$， $g_{\text{2}}^d\left(c\right)$ 三支曲线交于 $c_{\text{1}}$， $-g_{\text{2}}^a\left(c\right)$ 与 $g_{\text{2}}^b\left(c\right)$ 交于 $c_3$， $c_{\text{4}}$， $-g_{\text{2}}^a\left(c\right)$ 与 $g_{\text{2}}^d\left(c\right)$ 交于 $c_0$。

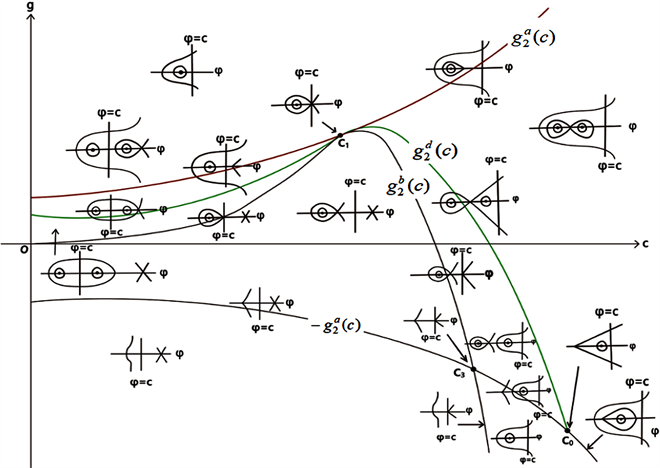
Figure 1. Bifurcation phase portrait of system (41) when $n=\text{2}$, $b<0$

图1. 当 $n=\text{2}$， $b<0$ 时，系统(41)的分支相图

Figure 2. Bifurcation phase portrait of system (41) when $n=2$, $b=0$

图2. 当 $n=2$， $b=0$ 时，系统(41)的分支相图

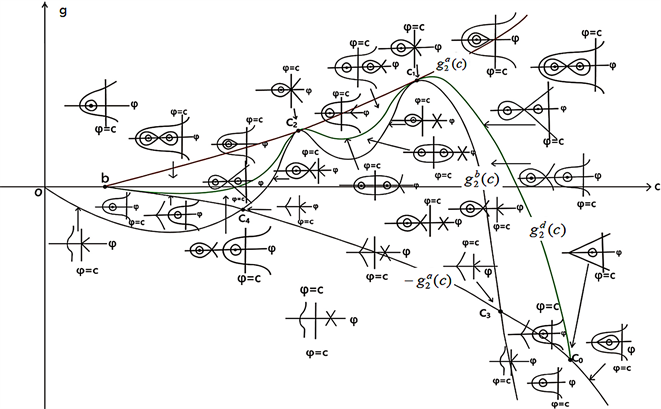
Figure 3. Bifurcation phase portrait of system (41) when $n=2$, $0<b<\frac{1}{4}$

图3. 当 $n=2$， $0<b<\frac{1}{4}$ 时，系统(41)的分支相图

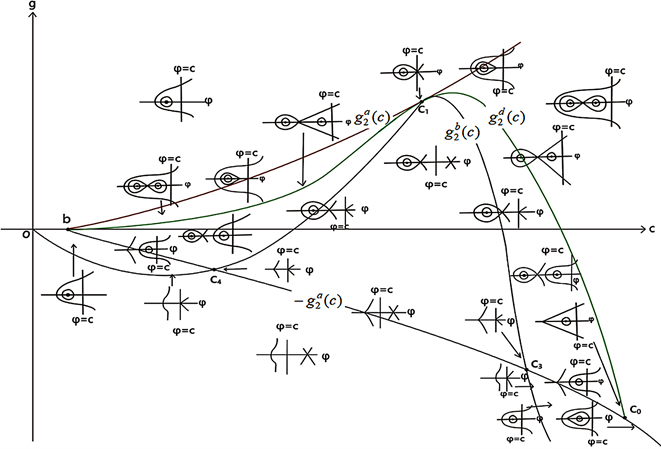
Figure 4. Bifurcation phase portrait of system (41) when $n=2$, $b=\frac{\text{1}}{\text{4}}$

图4. 当 $n=2$， $b=\frac{\text{1}}{\text{4}}$ 时，系统(41)的分支相图

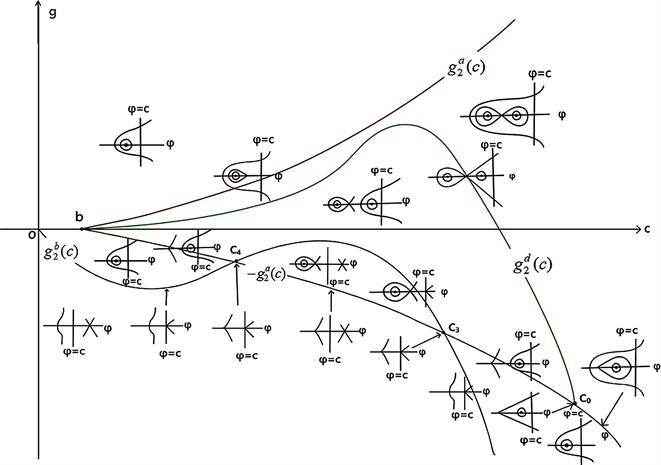
Figure 5. Bifurcation phase portrait of system (41) when $n=2$, $\frac{\text{1}}{\text{4}}<b<\text{1}$

图5. 当 $n=2$， $\frac{\text{1}}{\text{4}}<b<\text{1}$ 时，系统(41)的分支相图

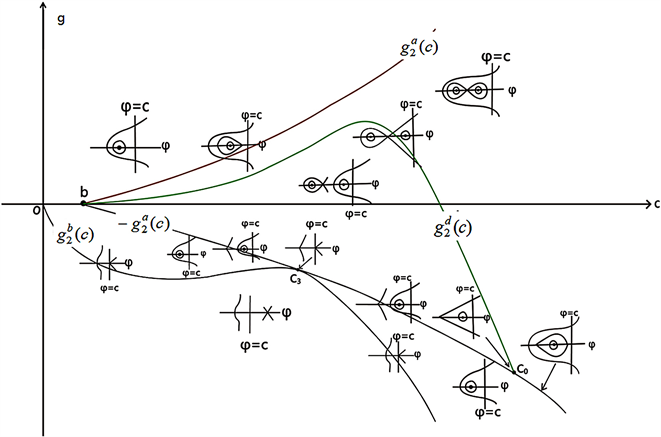
Figure 6. Bifurcation phase portrait of system (41) when $n=2$, $b=\text{1}$

图6. 当 $n=2$， $b=\text{1}$ 时，系统(41)的分支相图

5) 当 $\frac{\text{1}}{\text{4}}<b<\text{1}$ 时， $g_{\text{2}}^a\left(c\right)$， $g_{\text{2}}^b\left(c\right)$， $g_{\text{2}}^d\left(c\right)$ 无交点， $-g_{\text{2}}^a\left(c\right)$ 与 $g_{\text{2}}^b\left(c\right)$ 交于 $c_3$， $c_{\text{4}}$， $-g_{\text{2}}^a\left(c\right)$ 与 $g_{\text{2}}^d\left(c\right)$ 交于 $c_0$。

6) 当 $b=\text{1}$ 时， $g_{\text{2}}^a\left(c\right)$， $g_{\text{2}}^b\left(c\right)$， $g_{\text{2}}^d\left(c\right)$ 无交点， $-g_{\text{2}}^a\left(c\right)$ 与 $g_{\text{2}}^b\left(c\right)$ 交于 $c_3$， $-g_{\text{2}}^a\left(c\right)$ 与 $g_{\text{2}}^d\left(c\right)$ 交于 $c_0$。

7) 当 $b>\text{1}$ 时， $g_{\text{2}}^a\left(c\right)$， $g_{\text{2}}^b\left(c\right)$， $g_{\text{2}}^d\left(c\right)$ 无交点， $-g_{\text{2}}^a\left(c\right)$ 与 $g_{\text{2}}^b\left(c\right)$ 无交点， $-g_{\text{2}}^a\left(c\right)$ 与 $g_{\text{2}}^d\left(c\right)$ 交于 $c_0$。

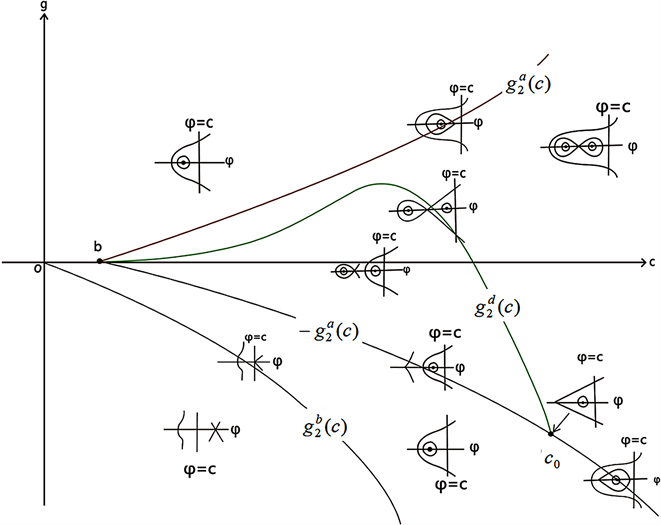
Figure 7. Bifurcation phase portrait of system (41) when $n=2$, $b>\text{1}$

图7. 当 $n=2$， $b>\text{1}$ 时，系统(41)的分支相图

6. 当n = 3时的分支相图

$g_{\text{3}}^a\left(c\right)=\frac{\text{3}}{\text{4}}{\left(c-b\right)}^{\frac{\text{4}}{\text{3}}}$ (52)

$g_{\text{3}}^b\left(c\right)=-\frac{1}{\text{4}}{c}^{\text{4}}+c^2-cb$ (53)

$\begin{array}{l}{g}_3^d\left(c\right)=\frac{1}{40}(-12bc+12c^2-\frac{63}{125}{c}^4-\frac{q}{13500}c+\frac{2916}{125}l{c}^7-\frac{243}{125}{l}^{\frac{2}{3}}{c}^6+36b{l}^{\frac{1}{3}}{c}^3\\ +\frac{126}{125}{l}^{\frac{1}{3}}{c}^5+\frac{2}{3}\left(c-b\right)l^{\frac{1}{3}}-\frac{7}{375}{\left(\frac{1}{l}\right)}^{\frac{1}{3}}{c}^3-\frac{1}{1500}{\left(\frac{1}{l}\right)}^{\frac{2}{3}}{c}^2)\end{array}$ (54)

其中p，q，l分别由式子(21)，(22)，(24)给出，图中点 $c_{\text{3}}^{\text{1}}$， $c_{\text{3}}^{\text{2}}$ 为 $g_{\text{3}}^a\left(c\right)$， $g_{\text{3}}^b\left(c\right)$ 和 $g_{\text{3}}^d\left(c\right)$ 三支曲线的交点，由方程(27)决定。具体情况如下：

1) 当 $b<0$ 时， $g_{\text{3}}^a\left(c\right)$， $g_{\text{3}}^b\left(c\right)$ 和 $g_{\text{3}}^d\left(c\right)$ 交于 $c_{\text{3}}^{\text{2}}$。

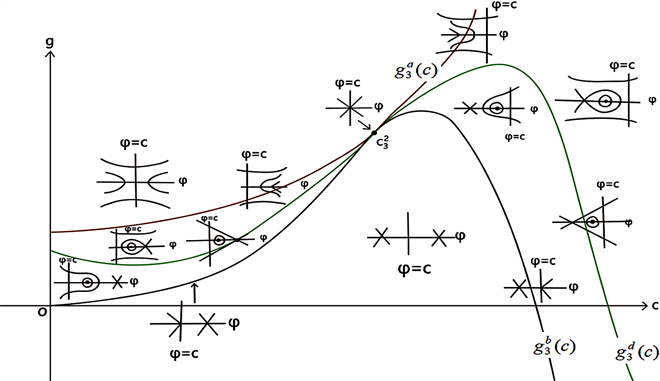
Figure 8. Bifurcation phase portrait of system (41) when $n=3$, $b<0$

图8. 当 $n=3$， $b<0$ 时，系统(41)的分支相图

2) 当 $b=0$ 时， $g_{\text{3}}^a\left(c\right)$， $g_{\text{3}}^b\left(c\right)$ 和 $g_{\text{3}}^d\left(c\right)$ 交于 $c_{\text{3}}^{\text{2}}$。

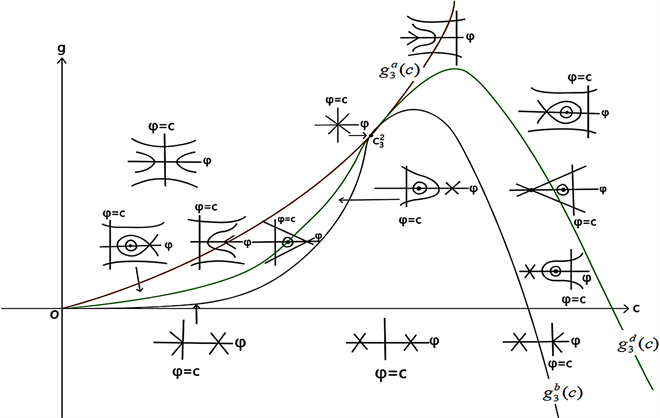
Figure 9. Bifurcation phase portrait of system (41) when $n=3$, $b=0$

图9. 当 $n=3$， $b=0$ 时，系统(41)的分支相图

3) 当 $0<b<\frac{\text{2}}{\text{3}\sqrt{\text{3}}}$ 时， $g_{\text{3}}^a\left(c\right)$， $g_{\text{3}}^b\left(c\right)$ 和 $g_{\text{3}}^d\left(c\right)$ 交于 $c_{\text{3}}^{\text{1}}$， $c_{\text{3}}^{\text{2}}$。

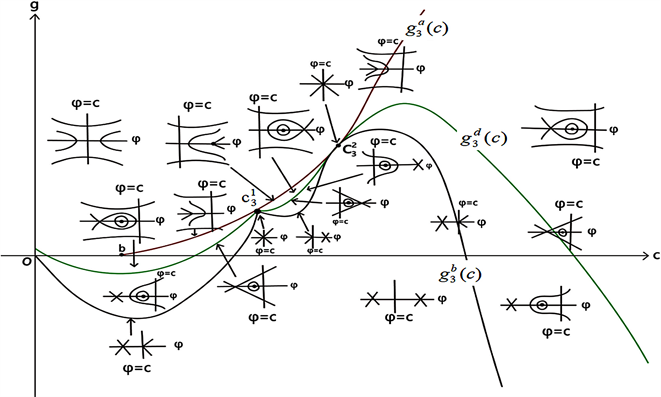
Figure 10. Bifurcation phase portrait of system (41) when $n=3$, $0<b<\frac{\text{2}}{\text{3}\sqrt{\text{3}}}$

图10. 当 $n=3$， $0<b<\frac{\text{2}}{\text{3}\sqrt{\text{3}}}$ 时，系统(41)的分支相图

4) 当 $b=\frac{\text{2}}{\text{3}\sqrt{\text{3}}}$ 时， $g_{\text{3}}^a\left(c\right)$， $g_{\text{3}}^b\left(c\right)$ 和 $g_{\text{3}}^d\left(c\right)$ 交于 $c_{\text{3}}^{\text{1}}$。

Figure 11. Bifurcation phase portrait of system (41) when $n=3$, $b=\frac{\text{2}}{\text{3}\sqrt{\text{3}}}$

图11. 当 $n=3$， $b=\frac{\text{2}}{\text{3}\sqrt{\text{3}}}$ 时，系统(41)的分支相图

5) 当 $b>\frac{\text{2}}{\text{3}\sqrt{\text{3}}}$ 时， $g_{\text{3}}^a\left(c\right)$， $g_{\text{3}}^b\left(c\right)$ 和 $g_{\text{3}}^d\left(c\right)$ 无交点。

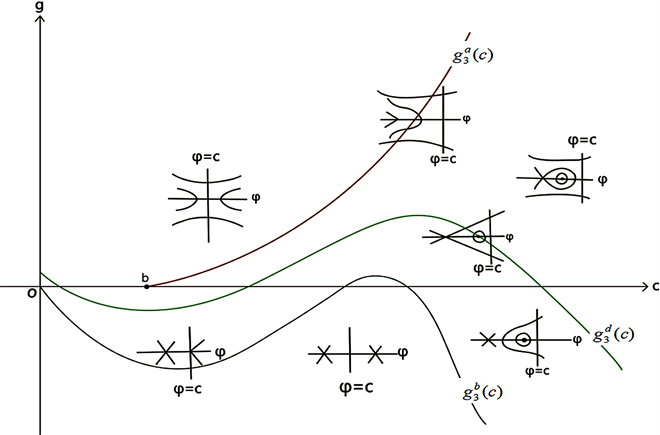
Figure 12. Bifurcation phase portrait of system (41) when $n=3$， $b>\frac{\text{2}}{\text{3}\sqrt{\text{3}}}$

图12. 当 $n=3$， $b>\frac{\text{2}}{\text{3}\sqrt{\text{3}}}$ 时，系统(41)的分支相图

7. 解的具体推导

1) 当 $n=2$， $g=g_2^d\left(c\right)$ 时，系统(41)的分支相图(见图1~7)，三个鞍点相连的相图中奇直线 $\phi =c$ 右侧的轨道有如下表达式

$y^2=\frac{\text{2}}{\text{15}}{\left(\phi -k+\frac{1}{4}c\right)}^2\left(\phi +2k+\frac{1}{4}c\right),c<\phi <+\infty ,且\text{0}<c<c_0,c\ne c_1,c_2$ (55)

其中 $c_{\text{0}}$， $c_1$， $c_{\text{2}}$，k分别由式子(6)，(7)，(8)，(9)给出。

将(31)带入(55)并沿着该轨道积分，得到

${\displaystyle {\int }_{\phi }^{+\infty }\frac{\text{d}s}{\left(s-k+\frac{1}{4}c\right)\sqrt{s+2k+\frac{1}{4}c}}}=\sqrt{\frac{\text{2}}{1\text{5}}}\left|\xi \right|$ (56)

求解方程(56)得到非线性波解 $u_1\left(x,t\right)$ 由式子(12)给出。

2) 当 $n=2$， $g=g_2^d\left(c\right)$ 时，系统(41)的分支相图(见图1~7)中连接三个鞍点的轨道有如下表达式

$y^2=\frac{\text{2}}{\text{15}}{\left(\phi -k+\frac{1}{4}c\right)}^2\left(\phi +2k+\frac{1}{4}c\right),-\frac{1}{4}c+k<\phi <c,且\text{0}<c<c_0,c\ne c_1,c_2$ (57)

其中 $c_{\text{0}}$， $c_1$， $c_{\text{2}}$，k分别由式子(6)，(7)，(8)，(9)给出。

将(31)带入(57)并沿着该轨道积分，得到

${\displaystyle {\int }_{\phi }^c\frac{\text{d}s}{\left(s-k+\frac{1}{4}c\right)\sqrt{s+2k+\frac{1}{4}c}}}=\sqrt{\frac{\text{2}}{1\text{5}}}\left|\xi \right|$ (58)

求解方程(58)得到非线性波解 $u_{\text{2}}\left(x,t\right)$ 由式子(13)给出。

3) 当 $n=2$ 时， $g=g_2^d\left(c\right)$，系统(41)的分支相图(见图1~7)中三个鞍点左侧的同宿轨有如下表达式

$y^2=\frac{\text{2}}{\text{15}}{\left(\phi -k+\frac{1}{4}c\right)}^2\left(\phi +2k+\frac{1}{4}c\right),-\frac{1}{4}c-\text{2}k<\phi <-\frac{1}{4}c+k,且\text{0}<c<c_0,c\ne c_1,c_2$ (59)

其中 $c_{\text{0}}$， $c_1$， $c_{\text{2}}$，k分别由式子(6)，(7)，(8)，(9)给出。

将(31)带入(59)并沿着该轨道积分，得到

${\displaystyle {\int }_{\phi }^{-\text{2}k-\frac{1}{4}c}\frac{\text{d}s}{\left(s-k+\frac{1}{4}c\right)\sqrt{s+2k+\frac{1}{4}c}}}=\sqrt{\frac{\text{2}}{1\text{5}}}\left|\xi \right|$ (60)

求解方程(60)得到非线性波解 $u_{\text{3}}\left(x,t\right)$ 由式子(14)给出。

4) 当 $n=2$， $g=g_2^d\left(c_{\text{0}}\right)$ 时，系统(41)的分支相图(见图1~7)中连接三个奇点的轨道有如下表达式

$y^2=\frac{\text{2}}{\text{15}}{\left(\phi +\frac{\text{1}}{\text{4}}c\right)}^{\text{3}},-\frac{\text{1}}{\text{4}}c<\phi <c,c=c_0$ (61)

其中 $c_{\text{0}}$ 由式子(6)给出。

将(31)带入(61)并沿着该轨道积分，得到

${\displaystyle {\int }_{\phi }^c\frac{\text{d}s}{{\left(s+\frac{1}{4}c\right)}^{\frac{3}{2}}}}=\sqrt{\frac{2}{15}}\left|\xi \right|$ (62)

求解方程(62)得到非线性波解 $u_{\text{4}}\left(x,t\right)$ 由式子(15)给出。

5) 当 $n=3$， $g=g_{\text{3}}^d\left(c\right)$ 时，系统(41)的分支相图(见图8~12)中连接三个鞍点的轨道有如下表达式

$y^2=\frac{\text{1}}{\text{12}}{\left(\phi -\gamma \right)}^2\left({\phi }^{\text{2}}+e\phi +f\right),\gamma <\phi <c,且\text{0}<c<+\infty ,c\ne c_3^1,c_3^2$ (63)

其中f， $\gamma$，e分别由式子(19)，(20)，(23)给出， $c_{\text{3}}^{\text{1}}$， $c_{\text{3}}^{\text{2}}$ 由方程(27)决定。

将(31)带入(63)并沿着该轨道积分，得到

${\displaystyle {\int }_{\phi }^c\frac{\text{d}s}{\left(s-\gamma \right)\sqrt{s^2+es+f}}}=\sqrt{\frac{\text{1}}{1\text{2}}}\left|\xi \right|$ (64)

求解方程(64)得到非线性波解 $u_{\text{5}}\left(x,t\right)$ 由式子(26)给出。

基金项目

广东省基础与应用基础研究基金资助(项目编号：2019B151502062)。