1. 引言
研究表明,笛卡尔空间的轨迹规划较为直观,便于任务决策层的任务分解规划,其拟合优化后虽解决了关节变量不平滑与加速度突变等问题,但是优化后所得轨迹存在较大的作业误差,且其速度与加速度变化幅度较大,影响作业的稳定性与可靠性,规划结果不理想,因此在关节空间中进行轨迹规划研究成为了主流研究趋势。对机械臂在关节空间中进行轨迹规划前,需要对其型值点事先完成逆运动学求解,其目的是将机械臂的位姿矩阵转换成其对应的关节角矩阵。逆运动学的求解具有计算量较大、计算复杂、存在多解性的特点,其求解方法目前主要包括几何法、解析法、数值法与人工智能法 [1] (启发式迭代法、神经网络学习法),几何法是最早出现的求解方法,通过利用平面间的几何关系,建立末端执行件位置参数与关节角之间的对应方程,完成求解计算 [2] [3]。解析法是目前应用最广泛的逆运动学求解方法,使用解析法对逆运动学求解前,需要事先对工业机器人的关节结构进行分析,该方法的前期准备工作量较大、需要对指定工业机器人进行单独求解,不具备泛用性,但求解速度最快,多用于在线计算场合 [4] [5] [6]。数值解法包括雅可比迭代法、牛顿迭代法和混合逆运动学求解法,数值法也是当下逆运动学研究的一个热点,具有求解速度快、精度高的优点,但其仍然存在求解单一的问题,即无法对所求解是否为最优逆解提出证明 [7] [8]。人工智能方法包含神经网络学习法与启发式迭代法两种类别 [9] [10] [11]。基于神经网络学习法的逆运动学研究,通过搭建神经网络平台,设定学习率,调节隐藏层神经元的层数及数量,设计合理的激励函数并输入大量学习案例,最终使该神经网络得到适当的权值与阈值,完成逆运动学求解工作。神经网络求解逆运动学的特点为求解速度极快,但求解成功率极不稳定,误差较大。针对神经网络求解逆运动学的研究主要集中于两个方面:一方面是采用不同类型的神经网络对逆运动学进行求解,以降低误差、提高求解成功率;另一方面是采用迭代法对神经网络的权值和阈值进行优化,以获得误差更低的神经网络模型。启发式迭代法通过采用不同的启发式算法,利用计算机的计算能力对逆运动学进行迭代求解,启发式迭代法求解逆运动学具有普适性广,求解速度中等,求解成功率稳定的特点,但其过大的计算量使其不适用于在线计算,只能采取离线计算的形式将求得的解通信传输给控制器,因此采用启发式迭代法进行求解时,工业机器人的运动具有明显的延迟性,并且对位姿矩阵数较多的求解中,该算法的计算效率较低,不如其他方法。
本文设计了一种带有灾变迁徙技术的小生境遗传算法用于逆运动学的求解计算,该算法在不考虑逆运动学多解性的情况下具有精度高、求解成功率稳定的特点,一定程度上克服了传统遗传算法的早熟与陷入局部最优解现象,对逆运动学求解具有实际工程意义。
2. 机械臂逆运动学求解问题
本文以PUMA560型机械臂为例展开研究,其标准D-H坐标参数如表1所示,其中,θi为关节角,αi-1为连杆扭转角,ai-1为连杆长度,di为连杆偏移距离。

Table 1. PUMA560 D-H parameter list
表1. PUMA560 D-H参数表
由机器人正运动学可知,标准D-H坐标系下,坐标系i-1到坐标系i间的位姿变换矩阵如式1所示:
(1)
依次连乘变换矩阵,便可以计算出机器人末端执行件与机器人基坐标系的变换关系,如式2所示:
(2)
位姿矩阵
是由表示执行件姿态信息的矩阵
及表达位置信息的矩阵
组成,如式3所示:
(3)
通过逆运动学反求出的关节角所对应的机械臂执行件位姿应最大程度接近给定目标位姿,因此优化的目标函数应当使所求位姿矩阵与目标位姿矩阵间的误差最小为目标,由于本次优化的目标函数是由关于机械臂位姿的12个参数累加而成,这会造成算法在收敛过程中容易被受到欺骗,造成本应同步逐渐收敛的12个值被其部分值得高速收敛所欺骗,造成了目标函数值病态减小的现象,因此在保证目标函数收敛性的同时,对目标函数包含的12个值的误差进行考察,若误差大于给定误差阈值则对该个体的适应度进行惩罚处理,避免优化陷入病态收敛。经仿真验证,对位置与姿态误差施加权重系数对避免优化陷入局部最优解也有积极的作用,因此调整后的目标函数为:
(4)
式中,k为位置与姿态间的权重系数,
为机械臂反求位姿矩阵中的值,
为机械臂给定目标位姿矩阵中的值,r为惩罚因子,其值由位姿矩阵的最大偏差确定,个体i的位姿矩阵最大偏差如式5所示:
(5)
若
,则惩罚因子
;若
,则惩罚因子
。为保证工业机器人运动过程中的安全性与可达性,还需对其关节位移的最大行程角度进行约束,即:
(6)
3. 逆运动学求解算法的设计
由于逆运动学当中关节角与位姿矩阵参数的映射关系复杂度较高,经仿真验证,传统小生境算法在求解逆运动学问题时效果有限。经研究发现,通过将遗传算法与不同的优化技术进行结合,可以对优化过程中出现的早熟现象及欺骗现象进行一定程度的避免,因此本文尝试将小生境遗传算法与种群迁徙技术与灾变境技术相结合,旨在于解决优化后期种群生境数过小的问题。将小生境技术、灾变技术、种群迁徙技术与遗传算法进行结合时,基于个体的编码方式不同,其距离计算的方法也不同,由于本文个体的生成方式为二进制编码生成,因此本文以不同个体间的海明距离作为依据对算法进行设计,算法主要实现步骤如下:
1) 生成种群:确定优化参数的个数及其上下界,本次编码基于二进制进行。对于6R型工业机器人而言,经解码后的一组个体数值信息可表示为:
(7)
2) 计算目标函数值:对种群编码进行解码处理,将解码后的数值利用式1计算其位姿并得到如式2形式的矩阵,计算个体位姿矩阵与期望位姿矩阵的误差和,得到目标函数值。
3) 种群生境划分:本次种群的个体基因基于二进制编码构成,其代码均由0、1两个数字表示,因此在对种群个体进行小生境划分前,需要先计算其不同个体间的海明距离,个体i与个体j之间的海明距离计算公式如式8所示:
(8)
式中,n为单个个体的基因占位数,
表示个体i经解码后解染色体上第k位的值(0或1),完成海明距离计算后,便可以将个体间间海明距离小于生境阈值的个体划分为同一生境。
4) 计算适应度:遗传算法的自身评定依赖于适应度值,根据个体的目标函数值可以计算出个体具有的适应度,个体i的适应度可由式9计算:
(9)
为避免早熟现象,小生境遗传算法需要对同生境中较劣个体的适应度进行惩罚,对于海明距离越小的两个个体,其适应度惩罚值应越大,故本次惩罚函数以同生境下不同个体间的海明距离为依据进行设计,对同一个小生境t的下的个体其惩罚函数如式10所示:
(10)
式中,
为该生境除适应度最高个体以外其余个体i的适应度,
分别为小生境中t中,所有个体与适应度最高(最优)个体的海明距离中的最大值、最小值和个体i与最优个体间的海明距离差值,α为最小惩罚系数,
为经过惩罚处理之后得到的新的适应度值。
5) 选择:本文采用轮盘赌的方式对个体进行选择操作。
6) 交叉:本文以生境为依据对其采用两种不同的交叉策略,生境内采用Partial-Mapped Crossover (PMX),生境外采用Multi-Point Crossover (MPX)。
7) 变异:由于逆运动学求解问题的复杂性,本文在传统变异的基础上,加入灾变技术与种族迁徙技术。
8) 淘汰:将生成的子代种群与父代种群结合,根据个体的目标函数值重新计算个体适应度、划分生境并对个体适应度施加惩罚函数,以适应度为依据采用精英淘汰制保留与父代种群个体数相同的个体,其余个体进行淘汰。
9) 终止条件:当迭代次数达到最大迭代次数、误差达到给定预期精度时或最优解一定次数不再更新时,终止迭代程序,将种群中的最优个体作为近似最优解输出,否则重复执行(5)~(8)。
4. 实验验证
基于MATLAB软件强大的计算能力,本次仿真在MATLAB软件环境下进行。为验证该算法搜索性能,本次仿真将PUMA560型机械臂所有关节的运动范围都设为最大值,即每个关节角的运动范围都为
,进一步扩大搜索空间,加大搜索难度。本次遗传算法的参数设置为:种群数150,迭代次数300,交叉系数0.08,变异系数0.01,生境划分值10,当种群最优解迭代20次无变化时,将下一次迭代的变异系数调整为0.1,对个体进行灾变处理,当种群生境数小于5、迭代次数大于总迭代次数的三分之一且最优解经过10次迭代无变化时,启动种群迁徙机制,强制增大种群搜索范围。为了验证该算法的性能,本文采用普通小生境算法对逆运动学进行的求解,并作为对照组将收敛速度与精度与该算法进行对比。本次逆运动学求解给定目标关节角为:
,PUMA560型机械臂在该组关节角下对应的末端执行件位姿矩阵为:
采用本文设计的算法利用MATLAB软件对其进行逆运动学求解计算,优化求解得到的一组关节角值为:
与该组关节角对应的执行件位姿矩阵为:
该算法与传统小生境遗传算法的目标函数迭代曲线如图1所示,可以发现采用普通小生境遗传算法进行优化,优化在进行到45次左右时整个种群出现早熟现象,陷入局部最优解,而改进小生境遗传算法则并未出现该问题,可以完成逆运动学问题的顺利求解。
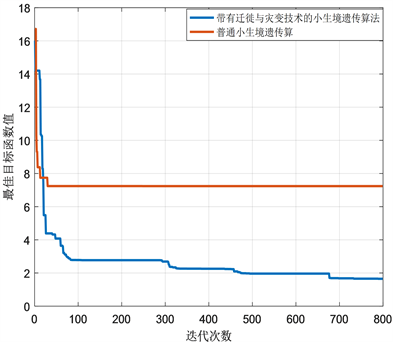
Figure 1. Optimal objective function iteration curve
图1. 最优目标函数迭代曲线
为了验证逆运动学求解结果的精确性,通过正运动学计算给定关节角、改进小生境算法最优关节角与传统小生境算法最优关节角的位置及RPY角,进一步验证算法的求解精度,如表2所示,图2与图3分别为期望关节角与优化求得关节角所对应的P560型机械臂的臂型与位姿:

Table 2. PUMA560 end-effectors position and RPY angle
表2. PUMA560关节角位置及RPY角
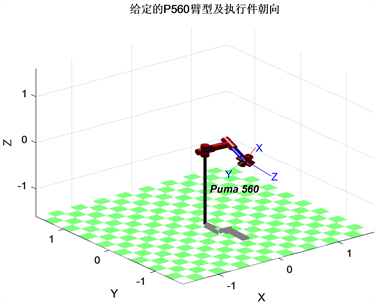
Figure 2. Desired arm shape and end-effector pose of PUMA560
图2. P560期望臂型及末端执行件位姿
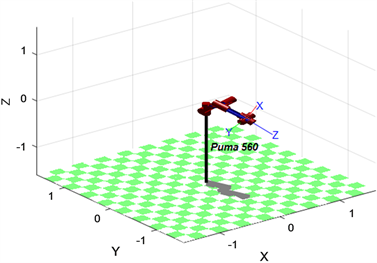
Figure 3. Optimal arm shape and end-effector pose of PUMA560
图3. P560优化臂型及末端执行件位姿
由表2可知,改进小生境算法求得的最优关节角精度较高,其位置误差均在5毫米内,RPY角度误差均在0.4˚以内,具有较高的求解精度,相比于传统小生境算法的求解,改进小生境算法明显具有更优的求解性能。
5. 结论
机械臂逆运动学在对机械臂的使用具有极大的意义,但关节角与位姿矩阵间的映射关系复杂度较高,求解过程具有一定难度。本文将小生境遗传算法与灾变技术、种群迁徙技术相结合,将经优化求解得到的关节角与给定关节角所对应的位姿矩阵进行比对,发现两组关节角所对应末端执行件的位置与姿态误差较小,证明该算法在优化过程中能够一定程度的克服求解过程中出现的早熟与欺骗现象,对避免优化陷入局部最优解起到了积极的作用,从而使得逆运动学的求解精度得到提高。利用计算机的计算性能采用算法进行逆运动学求解,极大降低了其求解难度,拓展了求解适应性,为逆运动学求解提供了便利。
基金项目
四川省科技计划项目(2019YFG0341)。