1. 引言
剪切模量是在材料弹性限度内剪切应力与剪切应变的比值,它是度量材料的力学性能重要指标 [1] 之一。钢丝的扭转角度、扭摆摆长和剪切模量之间的关系是普通物理中的重要力学关系。钢丝的剪切模量会随着扭摆摆长(或扭转角度)变化而变化,当摆长(或扭转角度)小于(或大于)某一长度(或某一角度),其测量值接近于某一定值即为此种钢丝的剪切模量理论值 [2]。本文通过测定不同长度的钢丝下悬挂的圆环、不同扭转角度的振动周期,计算对应角度的剪切模量 [3],利用origin软件绘出钢丝剪切模量和扭转角度及摆长之间关系的一簇曲线分析研究钢丝的扭转角度与摆长对实验结果的影响 [4] [5] [6]。本实验改进传统的实验装置,在扭摆的上部固定一个刻度盘,刻度盘上有0˚~720˚的刻度,以便更好的把握扭转角度,同时总结出扭转角大于300˚时测出的数据更接近于理论值。
2. 实验原理
实验扭摆结构如图1所示,刚性圆环横向放置在抓手上的方式如图2所示。如果将刻度旋钮围绕中心轴旋转一定角度
时,迅速将其再扭回原点,抓手就会受到钢丝弹性扭转力矩M的作用而作周期性振动,这就构成一个扭摆。
假设现有一个具有弹性的长方体体积元,如图1。(1) 剪切力 设弹性固体的一个长方形体积元,顶(底)面积为A,它的顶面固定,在它底面上作用着一个与顶面平行而且均匀分布的切力F (即剪切力),在力F作用下,两个侧面将转过一定角度
为剪切角。在
较小情况下,作用在单位面积上的切力F/A与剪切角
成正比。(1)式中,
(1)
G为剪切模量,表示材料抵抗剪切应变能力的常数,单位是N/m2,G值越大,说明该金属材料受到外力时的剪切角越小。(2) 扭转力矩 如图2所示,体积圆周所受的扭转力矩dM为
,应力存在而产生的总力偶距M为
,设圆柱体底部绕轴的转动角为
,而
,弧长
,
,故有
,圆柱体内的弹性力矩为
与外加力偶距M平衡时,
,可推出
,令
,
则有:
(2)
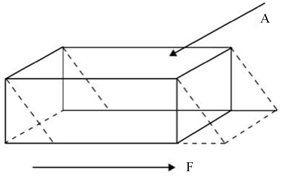
Figure 1. The schematic diagram of elastic solid
图1. 弹性固体切变示意图

Figure 2. The figure that the experimental
shear principle formula is deduced
图2. 实验原理公式推导用图
(2)式中:D为所测钢丝的扭转系数,用
表示钢丝在扭转振动中的角位移,抓手及圆环整个实验设
备对中心轴的转动惯量为
,根据转动定律有
,它的振动周期应是:
得出:
,测量出圆环水平放置在抓手上的扭转周期T1和爪上无负载时的周期T0,根据转动
惯量定理,剪切模量的测量公式可写为:
(3)
3. 实验方法
3.1. 实验准备
如图3所示,本实验通过自制角度盘测量钢丝的扭转角度,角度刻盘制作过程如下:在硬纸板上画半径大小不相等的两个同心圆;将圆心角等分成均匀的12份,每个角30度做出标记;将两个同心圆分别裁剪下来,取圆环部分,制作成本实验所需的角度刻盘。实验前对仪器进行调试、预热,并测量圆环的厚度、内外直径,钢丝的直径、长度和不同扭转角度的周期、扭摆空载周期等相关参量。

Figure 3. The appearance of the figure of the self-made angle plate
图3. 自制角度盘外观图
3.2. 实验过程
(1) 圆环质量(m/g):测得质量平均值m = 551.41 g;(2) 圆环内径(d1/cm):测得内直径平均值
;(3) 圆环外径(d2/cm):测得外直径平均值
;(4) 圆环厚度(dr/cm):测得厚度平均值
;(5) 钢丝直径(2R/mm):测得钢丝的直径平均值为0.400 mm;(6) 钢丝不同长度下,扭转周期和剪切模量,以钢丝扭转长度L = 40.0 cm时为例,实验时,逐渐增大扭转角度,增大梯度为30˚。记录抓手空载和横载时扭转10个周期所需时间,计算出扭转周期的平均值,记入表格中,再利用公式计算出钢丝的剪切模量。将钢丝的扭转角度和所计算的剪切模量数据输入origin软件,得到二者关系曲线如图4所示,图4中横轴
为钢丝的扭转角度,纵轴G为剪切模量。
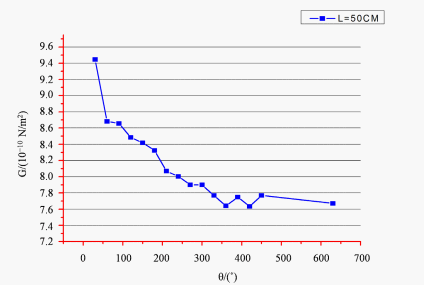
Figure 4. The figure of relationship between torsion angle and shear modulus when the torsion length is 50.0 cm
图4. 扭摆长度为50.0 cm时,扭转角度与剪切模量关系图
从图4可看出,随着角度从30˚逐渐变为360˚过程中(变化梯度为30˚),钢丝的剪切模量从大到小逐渐变化,最后趋于稳定的现象。用同样方法测量钢丝扭转长度L = 40.0 cm、60.0 cm、70.0 cm、80.0 cm时,扭转角度对应的周期及剪切模量,通过绘图软件分析其变化趋势。
4. 实验结论
把不同扭转角度对应的切变模量趋势图绘制在同一坐标系中如图5 (横轴
为钢丝的扭转角度,纵轴G为剪切模量):
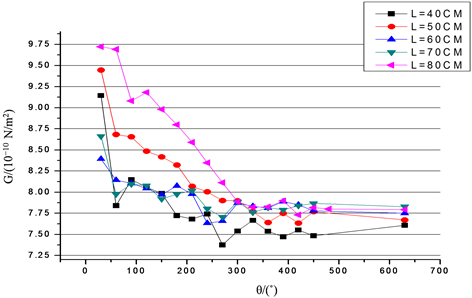
Figure 5. The figure of relationship between torsion angle and shear modulus of fine steel wire under different torsion length
图5. 不同扭摆长度下细钢丝的扭转角度和切变模量之间关系图
由图5看出:随着钢丝扭转角度逐渐加大,所测得的剪切模量小角度时以较快的速度变小,当钢丝的扭转角逐渐增大并大于300度时,剪切模量的测量值在7.8 × 10−10 N∙m−2上下波动,且随着钢丝的扭摆长度从小到大变化,剪切模量的变化范围逐渐变小;当扭摆长大于60.0 cm,小于70.0 cm时,小角度波动也不是很大,从0~360度范围内基本在理论值附近波动。随着摆长增加,扭转角度必须增大,才能更接近理论值7.8 × 10−10 N∙m−2;摆长在60.0 cm~70.0 cm时测得的剪切模量比较接近理论值7.8 × 10−10 N∙m−2。
本实验结果表明,钢丝扭摆长度和扭转角度对实验结果有较大的影响,钢丝的扭转角度需大于300˚、扭摆长度需大于60.0 cm且小于80.0 cm,才能得到较好的测量结果 [7]。对确定长度的钢丝,其扭转角度由小变大时,较小角度测得的剪切模量比较大角度时的相应值下降的快,表1是不同摆长、不同剪切模量的转折角(注:由小角度下降较快到大角度在理论值7.8 × 10−10 N∙m−2附近波动的转折角度称为“剪切模量转折角”):
从表1可看出,摆长在60.0 cm~70.0 cm之间的值更接近剪切模量的理论值,从而说明扭转角多大于300˚,摆长60.0 cm~70.0 cm之间能取得更好的实验效果。
5. 实验分析
本实验的系统误差包括量具本身的不准确和计时器的量化误差,如自制刻度盘、米尺、游标卡尺、千分尺、水准仪、多功能数字式计时器等。测量的随机误差是本实验的主要误差,相应的分析计算为:若用
表示随机误差,即
,式中xi表示测量值,本实验中为剪切模量的值Gi,
表示测量无限次平均值之差,这里可以用理论值
代替。以钢丝长度
,扭转角度300
度~630度多区间的剪切模量为例,单位为(10−10 N∙m−2),则其方差为:
,
方差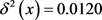 表示以钢丝长度
、扭转角度300度~360度区间的剪切模量随机误差的离散程度。剪切模量的标准差为:
有限次(如
次)剪切模量算术平均值和标准差计算:
表示以钢丝长度
、扭转角度300度~360度区间的剪切模量随机误差的离散程度。剪切模量的标准差为:
有限次(如
次)剪切模量算术平均值和标准差计算:
,实验标准差为:
,算术平均值标准差的估算值为:
。钢丝其他长度误差计算可以用同样方法进行,但误差离散程度须是比
较小的,在可接受范围内 [8]。

Table 1. The turning angles when the pendulum lengths and shear modulus are different
表1. 不同摆长、不同剪切模量时的转折角
6. 结语
通过使用剪切模量和转动惯量实验,测量不同扭转角度下、不同长度钢丝的扭转振动周期以研究扭转角和摆长对实验结果的影响。使用origin软件对测量数据进行分析,最终得出钢丝扭转角大于300˚时保证良好的实验测量精度。
课题名称
教育部高等学校大学物理课程教学研究立项项目(DJZW201934xn);六盘水师范学院《热学》精品课(LPSSYjpkc201605);六盘水师范学院大学生项目(LPSSYDXS19077);六盘水师范学院硕士学位培育点学科建设项目(LPSSYSSDYPY201704);关于混合式教学模式下的大学物理课程教学实践和应用(2018520116);六盘水师范学院大学生项目(LPSSYDXS19078)。
NOTES
*第一作者。