基于偏最小二乘回归的养老床位数预测研究

Prediction of Nursing Beds Based on Partial Least Squares Method

摘要: 构建和完善社会养老保障体系是应对人口老龄化的重要战略手段，是关乎民生的重大工程。养老床位是重要的养老资源，精准预测养老床位数具有重要意义。首先，文章选取国内生产总值、人均卫生费用、社区服务机构数、老年人抚养比等与养老床位数相关的15个指标。其次，根据留一交叉验证法，选取4个主成分，建立偏最小二乘回归模型以预测我国养老床位总数，并对回归系数和回归方程进行显著性检验。最后，以总的均方百分比误差(RMSPE)和平均绝对百分比误差(MAPE)作为模型评价指标，将偏最小二乘回归和逐步回归模型进行对比。结果表明：与养老床位数规模显著相关的指标为：社区服务机构数、离退人员参加养老保险人数、医疗保险基金支出、城镇职工基本养老保险累计结余、城镇居民人均可支配收入、城镇居民人均可支配收入等；偏最小二乘回归在预测养老床位数方面比逐步回归具有更好的预测效果。

Abstract: Building and improving the social security system for the elderly are an important strategic means to deal with the aging of the population, and it is a major project related to people’s livelihood. Pension beds are an important resource for the elderly, and accurate prediction of the number of beds for the elderly is of great significance. First, the article selects 15 indicators related to the number of elderly care beds, such as GDP, per capita health expenditure, number of community service agencies, and elderly dependency ratio. Secondly, according to the leave-one-out cross-validation method, four principal components are selected, a partial least squares regression model is established to predict the total number of quasi-care beds in my country, and the regression coefficient and regression equation are tested for significance. Finally, the total mean square percentage error (RMSPE) and average absolute percentage error (MAPE) are used as model evaluation indicators to compare partial least squares regression and stepwise regression models. The results show that the indicators that are significantly related to the scale of pension beds are: number of community service agencies, number of retired persons participating in pension insurance, medical insurance fund expenditure, accumulated balance of basic pension insurance for urban employees, per capita disposable income of urban residents, per capita urban residents, disposable income, etc. Partial least squares regression has a better predictive effect than stepwise regression in predicting the number of retirement beds.

1. 引言

我国国情现状中，人口老龄化呈现出增速态势 [1]，“21世纪的中国将是一个不可逆转的老龄社会” [2]。老龄化问题带来一系列问题，比如空巢、医疗卫生支出增加等，这些都是社会前进发展必须解决的问题。机构养老是解决人口老龄化的趋势，机构养老床位是最重要的资源。根据客观因素，精确地预计养老床位数，有利于养老机构进行养老床位数的安排与调整，既满足市场需求又避免床位浪费，从而推动养老产业的发展，具有丰富的现实意义。

国家高度重视养老问题，民政部、国家发展改革委制定《民政事业发展第十三个五年规划》，提出“到2020年每千名老年人口拥有养老床位数达到35至40张” [3]。已有大量的学者针对养老床位相关问题展开研究。王莉莉(2014) [4] 基于全国老年人口状况抽样调查及民办养老机构调查数据研究发现，城乡养老机构床位存在数量性和结构性短缺问题。康蕊(2016) [5] 基于对北京市养老机构服务数据统计分析发现，养老机构服务供给和老年人需求间存在结构性矛盾。崔树义(2017) [6] 等人基于山东省45家养老机构的调查发现，养老机构在发展过程中存在养老床位空置率高的问题。徐俊(2019) [7] 等人采用多元线性回归方法，以北京市为例研究养老床位使用率及其影响因素，研究发现真正对养老床位使用率显著影响的因素是养老机构所在位置、实际床均护理人数等，而与服务项目、费用等无关。杨红燕(2020) [8] 等人基于全国县级行政区域养老机构床位数据研究，验证了养老资源供给分布不均衡的根本原因在于政府间竞争与参照学习导致的财政支出结构偏向。从全国角度入手，给出养老床位预测的相关研究较少，而从全国角度精确预测养老床位数，有利于国家和养老机构合理拟定养老床位总数指标，因此开展相关研究是必要的。

与养老床位预测相关的指标多来自于经济、社会方面，而这些方面的指标间往往相互影响，因此如果直接使用这些指标进行建模，容易出现多重共线性问题。S. Wold和C. Albano [9] 等人为解决化学分析中多重相关的问题，提出偏最小二乘法。近年来，偏最小二乘法被扩展应用到自然、社会科学等众多领域 [10] [11] [12]。因此，基于偏最小二乘回归研究养老床位预测问题，可以解决各指标间的多重共线性问题。此外，由于中国养老行业尚且在探索发展阶段，历史数据有限，而偏最小二乘法支持在指标个数多于样本个数情况下进行回归建模。综上所述，基于偏最小二乘法预测养老床位数是有优势的。

本文选取与养老床位预测相关的15个指标，包括：国内生产总值、人均卫生费用、社区服务机构数、老年人抚养比等。根据留一交叉验证，确定主成分个数，建立偏最小二乘回归模型，以预测养老床位数，再对回归系数和回归方程进行显著性检验，找到主要与养老床位预测显著相关的指标。最后，采用RMSPE和MAPE作为模型评价指标，将偏最小二乘回归模型与逐步回归模型进行对比，对比找到在预测养老床位数时相对更合适的模型。

2. 养老床位需求指标体系构建

2.1. 养老床位数相关数据预处理

2.1.1. 数据收集与预处理

根据我国基本国情，我们考虑从政治、经济、人口状况方面着手开展研究，主要选取影响指标如下表1所示。根据我国国情，短期内，城镇居住的老人选择养老机构进行养老的可能性大于农村居住的老人选择养老机构进行养老的可能性，因此，我们优先考虑与城镇居民相关的指标，比如：城镇职工基本养老保险累计结余。本文建立模型时训练集和验证集所使用的数据为2009年到2018年官方记录数据，数据来自国际统计局官方数据(http://data.stats.gov.cn/)与中华人民共和国民政部统计公报(http://www.mca.gov.cn/article/sj/tjgb/)等，对暂无官方数据的指标进行插值处理。

Table 1. Influence index and symbol description of number of pension

表1. 养老床位数影响指标及符号说明

2.1.2. 描述性统计分析

对于所有指标进行描述性统计分析：通过寻找各指标在2009年到2018年的最值，可以看出各指标取值的波动范围；通过计算各指标的均值、标准差、偏度和峰度，可以得知各指标的平均水平以及波动程度。具体结果展示如表2。

Table 2. Results of descriptive analysis

表2. 描述性分析结果

通过上表2可看出，2009年到2018年，国内生产总值的最小值为348,518亿元，最大值为919,281亿元，均值为621,025.3元。从标准差角度看数据波动程度：人均国内生产总值、老年抚养比的取值波动较小。在倾斜程度上与正态分布相比：国内生产总值、在职职工参加养老保险人数、离退人员参加养老保险人数、参加养老保险人数、年末参加保险人数的数据分布相对左偏；社区服务机构数的数据分布与正态分布的偏斜程度相近；其余各指标的数据分布相对右偏。在陡峭程度上与正态分布相比：居民消费价格指数的数据分布相对较为陡峭，为尖顶峰；医疗保险基金支出数据分布与正态分布的陡缓程度相同；其余指标的数据分布相对平缓，为平顶峰。但是，因为现有的数据量有限，这些指标实际服从的分布仍可能为正态分布。

2.1.3. 数据标准化

在进行养老床位预测时，为了使得各方面因素的数据具有可比性，使得每个特征的重要性更加均衡，需要进行数据标准化从而消除变量之间的量纲关系。具体公式如下：

$y_i^{*}=\frac{y_i-\bar{y}}{s_y}$ (1)

$x_{ij}^{*}=\frac{x_{ij}-\overline{x_j}}{s_{x_j}}$ (2)

式中： $y_i$ 表示第i个样本中各类养老床位数样本数据； $x_{ij}$ 表示第i个样本中第j个自变量的样本数据。

假设养老床位数 $\tilde{y}$ 和各指标 $\widetilde{x_1},\widetilde{x_2},\cdots ,\widetilde{x_p}\left(p=1,2,\cdots ,14\right)$，共有n组观测数据，将原始数据标准化后记为：

$y=\left(\begin{array}{c}{y}_1\\ ⋮\\ y_n\end{array}\right),X=\left(\begin{array}{ccc}{x}_{11}& \cdots & x_{1p}\\ ⋮& \ddots & ⋮\\ x_{n1}& \cdots & x_{np}\end{array}\right)$ (3)

2.2. 相关性分析

通过相关分析探索各类养老床位总数与各自变量之间的密切程度，采用Pearson相关系数法计算得到各类养老床位总数与各指标的相关系数如表3。

Table 3. Correlation coefficient of the number of beds for the aged

表3. 养老老床位数指标体系相关系数

当Pearson相关系数的绝对值大于0.8时，认为这两个变量之间高度相关。根据上表得知：养老床位数与居民消费价格指数之间的相关系数为−0.16，该指标与养老床位数的相关性较弱，将该指标剔除。其余14个指标与各类养老床位总数之间的相关系数均大于0.9，因此，我们选择根据剩余的14个指标用于预测养老床位数。

2.3. 多重共线性诊断

假设 $x_{\left(1\right)},x_{\left(2\right)},\cdots ,x_{\left(n\right)}$ 是指标 $X_1,X_2,\cdots ,X_n$ 标准化后得到的向量，其中P为指标个数，在这里即为14。方阵 $X^{\text{T}}X$ 的条件数是度量多重共线性的一个重要指标，方矩 $X^{\text{T}}X$ 的条件数的计算公式如(14)。一般认为若 $\tau >1000$，则模型中自变量间存在严重的多重共线性，此时不可以直接利用这些自变量进行建模，否则会出现参数估计量含义不合理等问题，使得模型的预测功能失效。

$\tau \left(X^{\text{T}}X\right)=\frac{{\lambda }_{\max }\left(X^{\text{T}}X\right)}{{\lambda }_{\min }\left(X^{\text{T}}X\right)}$ (4)

式中： ${\lambda }_{\max }\left(X^{\text{T}}X\right)$, ${\lambda }_{\min }\left(X^{\text{T}}X\right)$ 表示方阵 $X^{\text{T}}X$ 的最大、最小特征值。

利用R语言计算由14个自变量组成向量 $X=\left(X_1,X_2,\cdots ,X_{14}\right)$ 得到方阵 $X^{\text{T}}X$ 的条件数为5.110909 × 10¹⁷。5.110909 × 10¹⁷远大于1000，与各类养老床位数高度相关的14个自变量间存在严重的多重共线性。

3. 基于偏最小二乘回归的养老床位需求实证分析

3.1. 偏最小二乘回归原理

假设养老床位数和各指标均已经按照式(1)(2)进行标准化，将结果记为式(3)。

将y对每个指标 $x_i$ 单独进行回归，即：

$\hat{y}\left(x_i\right)=\frac{x_i^{\text{T}}y}{x_i^{\text{T}}{x}_i}{x}_i,x_i=\left(\begin{array}{c}{x}_{1i}\\ ⋮\\ x_{ni}\end{array}\right),i=1,2,\cdots ,p$ (5)

其中 $x_i$ 表示资料向量， $x_i$ 表示影响养老床位数的指标。

取权 $w_i=x_i^{\text{T}}{x}_i$，令 $t_1={\displaystyle \underset{i=1}{\overset{p}{\sum }}{w}_i\frac{x_i^{\text{T}}y}{x_i^{\text{T}}{x}_i}{x}_i}={\displaystyle \underset{i=1}{\overset{p}{\sum }}\left(x_i^{\text{T}}y\right)x_i}$，则得到n个资料为 $t_1={\displaystyle \underset{i=1}{\overset{p}{\sum }}\left(x_i^{\text{T}}y\right)x_i}$。现在令 $t_1$ 为自变量，让y与 $t_1$ 建立回归方程，即

$\hat{y}\left(t_1\right)=\frac{t_i^{\text{T}}y}{t_i^{\text{T}}{x}_i}{t}_i$ (6)

得到y的预测向量 $\hat{y}\left(t_i\right)$，表达式为：

$\hat{y}\left(t_1\right)=\frac{t_i^{\text{T}}y}{t_i^{\text{T}}{x}_i}{t}_i$ (7)

将残差表示为 $y^{\left(1\right)}=y-\hat{y}\left(t_1\right)$。同样，让每个自变量 $x_i$ 对 $t_1$ 进行回归，得到回归方程，即：

${\hat{x}}_i\left(t_1\right)=\frac{t_1^{\text{T}}{x}_i}{t_1^{\text{T}}{t}_1}{t}_1,i=1,2,\cdots ,p$ (8)

利用上式，得到预测值，即：

${\hat{x}}_i\left(t_1\right)=\frac{t_1^{\text{T}}{x}_i}{t_1^{\text{T}}{t}_1}{t}_1,i=1,2,\cdots ,p$ (9)

将残差表示为 $x_i^{\left(1\right)}=x_i-{\hat{x}}_i\left(t_1\right),i=1,2,\cdots ,p$。

再将 $y^{\left(1\right)},x_1^{\left(1\right)},\cdots ,x_p^{\left(1\right)}$ 作为新的原始资料，重复操作，逐步求得 $t_1,t_2,\cdots ,t_r$，其中 $r=rank\left(X^{\text{T}}X\right)$。最后利用y对 $t_2,t_3,\cdots ,t_r$ 使用普通最小二乘法进行回归，得到回归方程，即：

$y={\displaystyle \underset{i=1}{\overset{r}{\sum }}{\alpha }_i{t}_i}$ (10)

进行变量转换，得到y关于 $x_1,x_2,\cdots ,x_p$ 的回归方程，即：

$y={\displaystyle \underset{i=1}{\overset{r}{\sum }}{\alpha }_i\left({\displaystyle \underset{j=1}{\overset{p}{\sum }}\left({\left(x_j^{\left(r-1\right)}\right)}^{\text{T}}{y}^{\left(r-1\right)}\right)x_j}\right)}={\displaystyle \underset{i=1}{\overset{r}{\sum }}{\beta }_i{x}_j}$ (11)

事实上，上式得到的是标准化后的养老床位数与各指标变量的回归方程，经过坐标变换：

$y=\frac{\tilde{y}-\overline{\stackrel{˜}{y}}}{s_{\tilde{y}}},x_i=\frac{{\tilde{x}}_i-{\overline{\stackrel{˜}{x}}}_i}{s_{{\tilde{x}}_i}},\left(i=1,2,\cdots ,p\right)$ (12)

其中： $\overline{\stackrel{˜}{y}},s_{\tilde{y}}$ 分别表示各类养老床位数样本均值和标准差； ${\overline{\stackrel{˜}{x}}}_i,s_{{\tilde{x}}_i}$ 表示各指标均值和标准差。

则得到未经过标准化的养老床位数 $\tilde{y}$ 和各指标 ${\tilde{x}}_1,{\tilde{x}}_2,\cdots ,{\tilde{x}}_p$ 的回归方程，即

$\tilde{y}={\displaystyle \underset{i=1}{\overset{p}{\sum }}{\tilde{\beta }}_i{\tilde{x}}_j}$ (13)

3.2. 模型参数的选择

3.2.1. 模型参数选择原理

采用留一交叉验证法，将全部数据集中的一个元素作为验证集，其余部分作为训练集。通过训练集拟合得到一个偏最小二乘模型，再将测试集中的数据代入拟合模型中，计算预测值误差平方和以及所有样本的预测值误差平方和称为PRESS，即

${\text{PRESS}}_i={{\displaystyle \sum \left(y_i-{\hat{y}}_i\right)}}^2$ (14)

$\text{PRESS}={\displaystyle \underset{i=1}{\overset{g}{\sum }}{\text{PRESS}}_i}$ (15)

3.2.2. 结果分析

根据表4，我们可以知道：当选取主成分个数为3时，对应的PRESS值(残差值)为0.1328；当选取主成分个数为4时，对应的PRESS值为0.06283，可以知道此时PRESS值迅速减小；当主成分个数为5时，对应PRESS值为0.08534，相对于四个主成分时，无较大变化。且当选取四个主成分时，此时PRESS总和最小。当选取4个主成分时，4个主成分对于因变量的累计贡献率为99.97%，对于因变量的累计贡献率为9.93%，即4个成分对各变量的累计贡献率均大于99%，因此我们最终选取4个主成分用于回归。

Table 4. Leave a cross validation result

表4. 留一交叉验证结果

下面将利用均方根图，从直观角度进行说明。当主成分个数从1变化到8时，均方根误差图如图1。根据均方根误差图，我们可以得知：当选定主成分的个数为4时，此时均方根误差较小，说明上面建模过程中选取4个主成分是合理的。

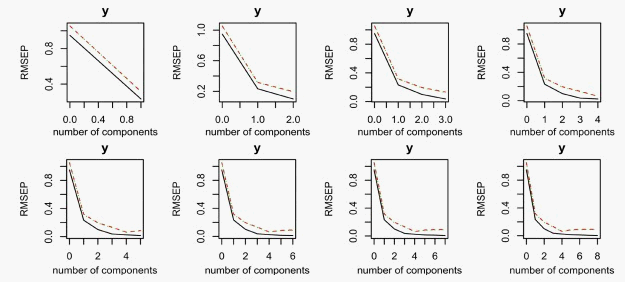
Figure 1. Root mean square error chart of partial least squares regression when the number of principal components is 1 - 8

图1. 主成分个数为1~8时偏最小二乘回归相应的均方根误差图

3.3. 偏最小二乘回归结果

根据Helland算法 [13]，我们得到已经过标准化的因变量y与主成分 $t_1,t_2,t_3,t_4$ 的回归方程，再带回各主成分对已经过标准化的自变量X的回归方程，经过坐标变换，即式(12)，最终得到因变量y与自变量X的回归方程。需要注意的是，得到的回归方程中，从直观上各指标前的系数可能存在与经验相违背的情况，这是由于实际变量之间具有重叠关系，相应自变量对因变量的影响可能通过其他变量已经表达出来。

3.4. 显著性检验

3.4.1. 回归系数显著性检验

对于模型参数的检验原理为：对于回归参数 $\beta$，原假设为 $\beta =0$，在原假设成立的条件下，统计量

$T=\frac{\hat{\beta }}{\hat{\sigma }\sqrt{c}}~t\left(n-p-1\right)$，其中：p指标个数，c为 $c={\left(X^{\text{T}}X\right)}^{-1}$ 对角线上的元素。在给定的显著性水平 $\alpha$ 下，当 $\left|T\right|\ge t_{\alpha /2}\left(n-p-1\right)$ 时，拒绝原假设，认为回归参数显著。对回归参数进行假设检验，结果如表5所示。根据表5，我们可以看到各类养老床位合计主要与社区服务机构数、离退人员参加养老保险人数、医疗保险支出显著相关。这说明，在进行预测养老床位时，要充分考虑相应地区的养老机构数、可能选择养老机构的老人总数以及养老机构的医疗卫生条件等。

Table 5. Partial least squares significance test table

表5. 偏最小二乘显著性检验表

3.4.2. 回归方程显著性检验

对于模型参数的检验原理为：对于所有的回归参数 ${\beta }_1,{\beta }_2,\cdots ,{\beta }_p$，原假设为 ${\beta }_1={\beta }_2=\cdots ={\beta }_p=0$，在原假设成立的条件下，统计量 $F=\frac{\text{SSR}}{\text{SSE}/\left(n-p-1\right)}~F\left(p,n-p-1\right)$，其中：p指标个数，SSR为回归平方和，SSE为残差平方和。在给定的显著性水平 $\alpha$ 下，当 $F\ge F_{\alpha }\left(p,n-p-1\right)$ 时，拒绝原假设，认为回归方程显著。

4. 养老床位需求模型精度比较

4.1. 基于逐步回归的养老床位需求预测

逐步回归原理及结果

逐步回归法是解决多重共线性的经典方法，逐步回归的基本思想是：一个个引入自变量，每当新引入一个变量时，便进行一次逐个检验。如果在新引入变量后，原变量不再显著，那么则将其剔除，最终保证模型中只含有显著的变量 [13]。下面我们将建立逐步回归模型，用于解决养老床位预测问题。本文利用SPSS软件实现逐步回归，最终得到模型：

$y=0.002\ast \text{NCSA}+67.870$ (16)

4.2. 模型对比

根据表6中的指标数据，对于2019年各类养老床位数合计进行预测：偏最小二乘回归结果为834.59张，逐步回归预测结果为991.34张。用两种回归预测结果取平均值代替2019年各类养老床位合计真实值。

Table 6. Related index data of number of nursing beds in 2019

表6. 2019年养老床位数相关指标数据

将偏最小二乘与逐步回归建立模型的拟合和预测效果作图2如下。根据图2中，直观上，我们可以看出预测养老床位时，通过偏最小二乘回归建模的拟合效果比逐步回归建模的拟合效果好。

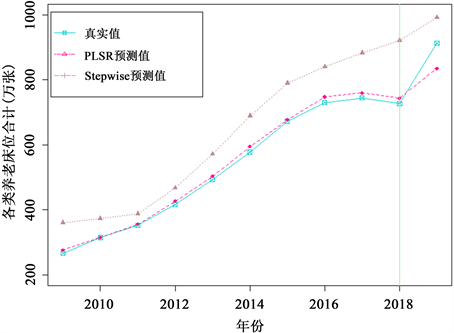
Figure 2. Comparison of partial least squares regression and stepwise regression models

图2. 偏最小二乘回归和逐步回归模型效果对比

根据总的均方百分比误差(RMSPE)和平均绝对百分比误差(MAPE)，对比偏最小二乘模型和逐步回归模型，RMSPE和MAPE的计算公式为(17) (18)。计算得到：经过偏最小二乘法建立的模型，RMSPE为0.0239，MAPE为0.0213；经过逐步回归的模型，RMSPE为0.2016，MAPE为0.1893。根据经验，当RMSPE和MAPE越小，模型精度越高，这说明偏最小二乘法得到的模型比逐步回归得到的模型精度高。

$\text{RMSPE}=\sqrt{\frac{1}{n}{\displaystyle \underset{k=1}{\overset{n}{\sum }}\left(\frac{{\hat{y}}^{\left(0\right)}\left(k\right)-y^{\left(0\right)}\left(k\right)}{y^{\left(0\right)}\left(k\right)}\right)}}\times 100\%,k=1,2,\cdots ,n$ (17)

$\text{MAPE}=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|\frac{{\hat{y}}^{\left(0\right)}\left(k\right)-y^{\left(0\right)}\left(k\right)}{y^{\left(0\right)}\left(k\right)}\right|}\times 100\%,k=1,2,\cdots ,n$ (18)

预测养老床位数时，逐步回归与偏最小二乘回归相比处于劣势的原因分析如下：根据逐步回归的结果，各类养老床位合计仅与指标社区服务机构数有关，而根据生活经验，影响养老床位数的原因是多面的。逐步回归的结果过于理想化，没有考虑到事物的普遍联系，偏离客观规律。

5. 结论

本文从客观角度上选择可能与养老床位预测相关的15个指标，根据留一交叉验证法，选定主成分个数为4时，进行偏最小二乘回归。进一步，通过对回归系数进行显著性检验，寻找到与预测养老床位数显著相关的因素为：社区服务机构数、离退人员参加养老保险人数、医疗保险基金支出等。利用SPSS软件建立逐步回归模型后，将偏最小二乘回归和逐步回归拟合和预测效果对比可视化，在进行预测养老床位数时，偏最小二乘回归模型比逐步回归模型具有一定优势。

根据偏最小二乘回归法计算出的结果来看，预测所需各类养老床位要充分考虑养老机构数、可能选择养老机构的老人总数以及养老机构的医疗卫生条件等方面的因素，同时为了提高现有的养老床位使用率，提出以下相关问题并给出解决方案：

养老机构服务设施有待改进。公办性质的养老院与民营的差距主要在于民营养老院基础设施条件比较差，医疗卫生存在短板。有需求选择养老机构的老人数量与实际选择养老机构的老人数量不相等，老人在选择养老机构时，通常会因以下几个方面受到影响：养老院的每月收费标准；老年人对于部分养老机构的评价较低；老年人在精神需求方面需求更高；部分老年人获得信息的渠道较少。

加强养老院机构基础设施建设以及提高医疗卫生条件。在养老院房屋建筑方面需要包括接待用房；满足老年人在养老院内生活起居方面需要的生活用房；可以为养老院内老年人提供一些常见疾病的诊断治疗及一般的卫生保健服务场所；在精神层面去满足老年人的文化娱乐休息用房；康复训练室；心理咨询室；临终关怀室等都应配备齐全。养老机构应满足更多老人对于养老的需求。在养老院收费标准方面进行明细公开，加以制度进行制约；在专业人才培养方面，严格要求，持证上岗；养老院方面应加强对精神文化方面的建设，提高相关基础建设，增加精神文化。