1. 引言
随着轨道交通车辆运行速度的不断提高,轮轨之间的动态作用增强。轮轨之间的相互作用会导致车轮不圆顺,对系统振动特性产生影响,造成零部件的损坏,严重时会危及行车安全。因此,有必要建立轮轨动力学分析模型,研究车轮失圆的多边形对轮轴系统振动的影响,为轮缘多边形的预测和控制提供理论基础。
轮缘多边形化是车轮不圆顺的一种表现形式,即车轮半径沿圆周方向呈现出周期性变化。轮缘多边形的边数即为车轮不圆的阶数。国内外学者针对车轮不圆顺进行了大量的研究。J C O Nielsen和A Johansson [1] [2] [3] 对前人早期的研究进行了总结,对车轮不圆顺的形式进行了分类。A Johansson和J C O Nielsen [4] 将现场试验和仿真分析相结合,得出了轮缘多边形对轮轨动态作用力的影响规律。Meywerk [5] 将轮轨进行弹性处理,建立了相应的动力学模型,对轮缘多边形的形成、发展过程进行了研究。
陈伟 [6] 等建立整车车辆动力学模型,探究了高阶车轮多边形对列车动力学性能的影响,结果表明车轮多边形对脱轨系数、平稳性指标影响较小,对轮轨垂向力影响较大。王天龙 [7] 研究了重载机车的车轮多边形演化规律,并且给出了车轮多边形波深控制建议。陶功权 [8] 等对B型地铁车轮不圆进行现场调研和仿真分析,给出了减缓车轮失圆的建议并提出了低阶车轮多边形的镟修限值。邢远 [9] 等考虑列车实际服役条件,建立了CRH3型列车的动力学模型,研究了车轮多边形阶数、波深以及行车速度对轮轨接触力的影响。王红兵 [10] 等建立考虑轮对柔性的刚柔耦合车辆动力学模型,并根据轮轨轮重减载率限值制定了相应工况下的车轮多边形幅值限值。
综上,虽然已有大量学者对车轮不圆顺的成因及对动力学特性的影响进行了分析,但车轮不圆顺对轮轴系统振动的影响依然较少。本文基于多体动力学理论建立考虑轮缘多边形的轮轨的动力学仿真模型,研究轮缘多边形对轮轴的振动影响,获得轮缘多边形对轮轴系统动力学的影响规律,为轮缘多边形导致的振动特性预测以及振动控制提供理论依据。
2. 轮缘多边形产生机理及表征
2.1. 轮缘多边形产生机理
轮缘多边形的产生的原因主要包括初始变形以及后期运转过程磨损导致。加工过程中工件和刀具在切削过程中的相互位置决定了加工后车轮的尺寸和几何形状 [11] [12]。因此系统中任何一个组成部分出现误差都将导致最终所加工的车轮出现误差,进而导致车轮不圆的出现,为初始多边形。
此外,车轮运行过程的磨损也会导致多边形甚至扩展演化,文献 [13] 指出车轮初始不圆的发展与车辆运行速度和轨道条件有关,常见的1~3阶初始不圆的磨耗发展规律下:车轮初始1阶不圆(偏心)经过长时间磨耗后,最终发展为3阶不圆;车轮初始2阶不圆(“椭圆化”)最终发展为4阶不圆;车轮初始3阶不圆的形状和相位没有发生变化,即没有向高阶不圆发展,只是磨耗程度不断加剧。在同样的速度和轨道条件下,车轮初始4阶不圆和初始5阶不圆也会向高阶不圆发展。随着车轮轮缘的磨耗,车轮半径不断减小,车轮滚动中磨耗的重复性被打破,不圆度的阶次向更高阶发展。
2.2. 轮缘多边形的特征
轮对弯曲共振导致的车轮不圆阶数取决于车轮滚动频率,也就是取决于车辆的运行速度与车轮半径,则:
(1)
式中,
为轮对弯曲共振频率,
为车轮旋转频率,v为车辆运行速度,单位km/h,r为车轮半径,单位m。
轨道不平顺的波长是固定的,车轮不圆阶数取决于车轮的周长。则:
(2)
式中,l为轨道不平顺波长,单位m;r为车轮半径,单位m。
列车运形时,多边形阶数n与钢轨冲击振动频率f关系为:
(3)
式中,v为车辆运行速度,n为多边形阶数,d为车轮直径。
由式3可知,轮轨间冲击产生的振动频率同车轮转动频率呈倍数关系。
3. 基于多体动力学的轮轨系统动力学模型
3.1. 轮轨动力学模型的建立
本文基于Pro-e软件建立三维轮轨接触模型,忽略构架、轴箱等结构,采用双轮和双边铁轨接触,将轨道简化成圆轮,其中车轮具有多边形形状,采用表1参数建立的模型如图1所示,将已经建立好的三维模型,导入ADAMS中建立车轮与铁轨接触的轮轴刚体动力学模型,并采用质量块模拟车体质量,设置质量块模拟车厢的重力作用,根据实际情况,质量块的设置为15吨。
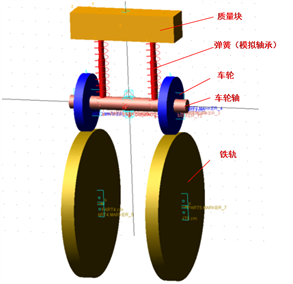
Figure 1. Wheel and axle multi-body dynamic model
图1. 轮轴多体动力学模型
本文分别建立车轮轮缘三阶多边形、二十一阶多边形(图2),分析对比不同阶次多边形对轮轴的振动影响。通常车轮多边形的波深一般最大值为0.9 mm,最小值为0.03 mm,本文选取多边形波深为0.5 mm。
材料属性如表2所示。
3.2. 约束和运动激励
1) 约束
将模型导入后,对各零部件的相对运动施加约束,具体约束设置如下表3所示。车轴与轴质量块施加垂直方向的移动副,轴与车轮、铁轨模拟轮1与大地施加旋转。
2) 运动激励和载荷
实际运行过程中,运动激励一般来自于旋转轴带动车轮一起运动,而铁轨是固定的。为了防止车轮与铁轨模拟轮之间出现干摩擦,对铁轨模拟轮也设置了运动激励。
列车的运行速度为v(km/h),则车轮的转动频率f(Hz)为:
(4)
式中,r为名义滚动圆的半径。
3.3. 接触力学模型
轮轨模型中的力学模型,包括以下几个方面:
1) 接触力的设置
车轮与铁轨接触时产生法向和切向的接触力。在ADAMS软件中,法向接触力采用罚函数法进行求解,切向接触力采用库伦摩擦方法进行求解。
本文采用冲击函数模型((Impact)进行计算,轮轨接触的法向接触力Impact函数表达式为:
(5)
式中,K为轮轨接触刚度系数;
为接触渗透量,
为最大允许穿透深度,选取0.1 mm;
为达到最大穿透深度时的最大接触阻尼,反映了碰撞时能量的损耗,取为刚度系数的1%。;e为非线性弹簧力的指数,轮轨之间接触为线接触,取为10/9。
接触刚度系数K采用赫兹接触理论计算:
(6)
式中,B是车轮的宽度。
2) 摩擦力学模型
车轮与铁轨之间产生的切向摩擦力采用库伦(Coulomb)计算,由摩擦因素是由静摩擦因
,动摩擦系数
和指数衰减系数DC组成,并认为
与接触表面的相对速度
有关。
(7)
考虑车轮的材料属性,动摩擦系数
为0.1,静摩擦系数
为0.3,动摩擦相对滑移速度
为10 m/s,最大静摩擦相对滑移速度
为0.1 m/s。
4. 结果与讨论
仿真条件,车轮和铁轨为恒定转速,具体转速如表3所示。设置仿真时间为1 s,仿真步长为1000步。

Table 3. Wheel and rail simulation wheel rotation frequency
表3. 车轮与铁轨模拟轮的转动频率
4.1. 车速为100 km/h时轮轴系统振动
1) 轮缘三阶多边形
车速在100 km/h时车轮轮缘三阶多边形的车轴径向加速度振动时域及频域图如图3所示,由图可以看出,车轮轴振动信号由多组冲击信号组成,这是由于车轮为三阶多边形,车轮每旋转一圈会与铁轨产生三次冲击。此外,在340 Hz、370 Hz、400 Hz、710 Hz处加速度幅值均有凸起,在370 Hz处,加速度的幅值最大,此时对应频率为车轮转动频率(10.3 Hz)的36倍频。
 (a) 时域图
(a) 时域图 (b) 频域图
(b) 频域图
Figure 3. 100 km/h Radial vibration acceleration of third-order polygonal axle
图3. 100 km/h三阶多边形车轴径向振动加速度
(2) 轮缘二十一阶多边形
车速在100 km/h时,车轮轮缘为二十一边形的车轴径向加速度振动时域及频域如图4所示,由图可以看出,车轮轴振动信号由多组冲击信号组成,但冲击信号幅值小于三边形车轮冲击信号幅值。此外,在216.3 Hz处,加速度幅值最大,为车轮转动频率(10.3 Hz)的21倍频,与多边形的边数一致。
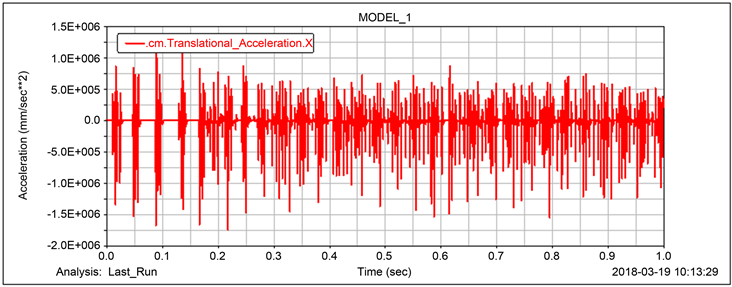 (a) 时域图
(a) 时域图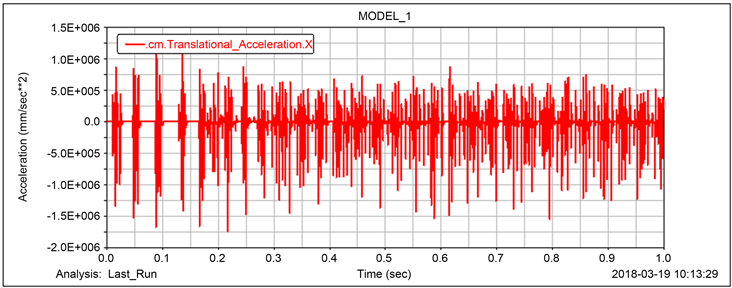 (b) 频域图
(b) 频域图
Figure 4. 100 km/h Radial vibration acceleration of twenty-first-order polygon axle
图4. 100 km/h二十一阶多边形车轴径向振动加速度
4.2. 车速为200 km/h轮轴系统振动
1) 轮缘三阶多边形
车速在200 km/h时车轮轮缘三阶多边形的车轴径向加速度振动时域及频域如图5所示,由图可以看出,车轮轴振动信号由多组冲击信号组成,这是由于车轮为三阶多边形,车轮每转一圈会与铁轨产生三次冲击。此外,在680 Hz、740 Hz、800 Hz处加速度幅值均有凸起。在740 Hz处,加速度的幅值最大,且740 Hz为车轮转动频率(20.6 Hz)的36倍频。
2) 轮缘二十一阶多边形
车速在200 km/h时,车轮为二十一边形的车轮轴径向振动加速度时域及频域如图6所示,由图可以看出,车轮轴振动信号由多组冲击信号组成,但冲击信号幅值小于三边形车轮冲击信号幅值,此外,在250.1 Hz、306.2 Hz、432.6 Hz处,加速度幅值均有凸起,且432.6 Hz为车轮转动频率(20.6 Hz)的21倍频,与多边形的边数一致,本文理论仿真得出结论与公式3得出和文献 [13] 中所提到结论相一致。
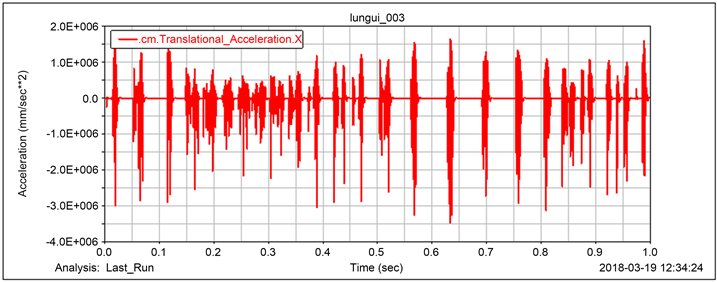 (a) 时域图
(a) 时域图 (b) 频域图
(b) 频域图
Figure 5. 200 km/h Radial vibration acceleration of third-order polygonal axle
图5. 200 km/h三阶多边形车轴径向振动加速度
 (a) 时域图
(a) 时域图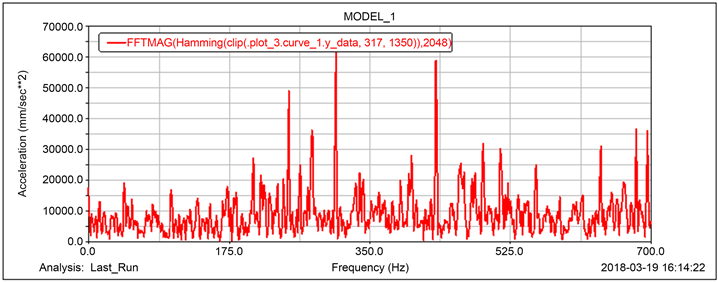 (b) 频域图
(b) 频域图
Figure 6. 200 km/h Radial vibration acceleration of 21-sided axle
图6. 200 km/h二十一边形车轴径向振动加速度
5. 结论
本文基于建立计入轮缘多边形的轮轨系统动力学仿真模型开展不同转速下轮缘多边形的阶次、车速对轮轴的振动影响研究,具体的结论如下:
1) 在多边形车轮波深相同的情况下,三阶多边形轮轴的径向振动幅值比二十一阶多边形车轮的径向振动幅值大。由此推断低阶多边形车轮对轮轴的振动影响较大。
2) 随着列车运行速度的增加,轮轴振动增大,且三边形增加幅度更大。
3) 当存在三阶车轮多边形时,加速度幅值在车轮转频36倍频处达到最大;当存在二十一阶车轮多边形时,加速度幅值在车轮转频21倍频处达到最大,与多边形阶数相同。
基金项目
本论文受到辽宁省自然科学基金(20180550792和20180551017)和大连市高层次支持计划(2018RQ18和2018RQ50)资助。
NOTES
*通讯作者。