光伏与柔直互联系统稳定性及其影响因素分析

Stability and Influencing Factors Analysis of PV and VSC-HVDC Interconnection System

摘要: 我国青海地区已建成并规划建设多个大型光伏电站，利用柔直将大规模光伏进行汇集是一种理想的方案，然而光伏逆变器和柔直整流器相互作用可能会引发振荡。为了分析光伏与柔直互联系统的稳定性，文中首先利用谐波线性化方法，在三相静止坐标系中建立了光伏与柔直互联系统的阻抗模型，然后利用理论分析与仿真相结合的方法，分析了光伏电站与柔直整流站接口处产生振荡的机理及其影响因素。理论分析和仿真结果表明，光伏逆变器和柔直整流器阻抗具有LC特性，两者会在某些频段下发生电气谐振，而使接口电压和电流产生振荡。光伏电站输出功率增加会使系统的稳定性降低，而柔直整流器电压外环控制器比例系数和锁相环比例系数增加会提高系统的稳定性。

Abstract: A number of large-scale PV stations have been built and planned to be built in Qinghai Province, and it is an ideal scheme to use VSC-HVDC to gather them; however, the interaction between PV inverter and VSC-HVDC rectifier may cause oscillation. In order to analyze the stability of PV and VSC-HVDC interconnection system, the harmonic linearization method is used to establish the impedance of it in three-phase static coordinate system, and then the mechanism and influencing factors of oscillation are analyzed by combining theoretical analysis and simulation. Theoretical analysis and simulation results show that the impedance of PV inverter and VSC-HVDC rectifier has LC characteristics, and they will have electrical resonance in certain frequency bands, which will cause oscillation of interface voltage and current. The stability of the system will be reduced with the increase of the output power of the PV station, while the increase of the proportion coefficient of the voltage controller of VSC-HVDC rectifier and the phase locked loop will improve the stability.

1. 引言

我国青海地区太阳能资源丰富，已建成并规划建设多个大型光伏电站。大型光伏电站多位于戈壁荒漠，远离交流主网，可以利用柔性直流输电技术(以下简称柔直)将大规模光伏进行汇集 [1] [2] [3]。电网实际运行情况表明，电力电子设备之间的耦合作用很有可能激发振荡，威胁设备安全 [4]。光伏经柔直汇集系统是一个典型的多电力电子设备系统，其中光伏逆变器和柔直整流器高度互联，同时两者控制器间存在强相互作用，这加剧了系统潜在的振荡风险。因此，研究光伏与柔直互联系统的稳定性及其影响因素具有重要科研和工程应用价值。

目前研究含电力电子换流器系统稳定性的方法主要集中在状态空间法和阻抗法 [5] [6] [7]。前者是一种时域的分析方法，通过建立系统的状态空间模型，分析系统矩阵的特征值分布，可以得到各参数对系统稳定性的影响。阻抗法是一种频域分析方法，求得系统中各子系统的阻抗模型后，可以利用奈奎斯特稳定判据分析系统的稳定性。基于以上方法，目前已有较多文献研究了光伏电站次同步振荡和柔直高频振荡问题：文献 [8] 认为，并网光伏逆变器在次同步频带可能会呈容性，其与阻感性的电网阻抗作用会诱发次同步振荡。文献 [9] 利用阻抗分析法，对弱电网条件下光伏逆变器并网系统的稳定性条件进行了分析，认为逆变器输出阻抗与电网阻抗在谐振频率处具有一定的相角裕度，才能使系统稳定运行。文献 [10] 认为柔直固有的链路延时特性会使其高频阻抗呈现“负电阻电感”特性，可能与长交流线路的分布电容相互作用导致高频振荡失稳现象发生。以上文献均认为光伏电站以及柔直的振荡问题，其实质都是换流器与电网阻抗相互作用而引发的不稳定问题，而光伏与柔直互联系统中，柔直直流电容隔离了电网阻抗对光伏逆变器和柔直整流器的影响，系统的稳定性取决于光伏逆变器和柔直整流器的相互作用，即换流器之间的相互作用。目前鲜有文章研究光伏与柔直互联系统中光伏和柔直相互作用而造成系统不稳定的问题。

为了分析光伏与柔直互联系统的稳定性，本文利用谐波线性化方法建立了系统的阻抗模型，分析了光伏电站与柔直整流站接口处发生振荡的机理，并采用奈奎斯特稳定判据分析了影响光伏与柔直互联系统稳定性的因素。PSCAD/EMTDC中算例系统的仿真结果验证了理论分析结果的正确性。

2. 光伏与柔直互联系统结构与控制

光伏与柔直互联系统的拓扑如图1所示。图中，光伏电站主要由光伏阵列、光伏逆变器p及其他并网环节组成；柔直主要由整流器r、逆变器i、直流电容、直流线路、换流变压器和滤波器等组成；母线N为光伏电站和柔直整流站的接口。

Figure 1. Topology of the PV and VSC-HVDC interconnection system

图1. 光伏与柔直互联系统拓扑

光伏与柔直互联系统的等效电路和控制系统结构如图2所示。其中，光伏逆变器为常规的三相桥式电压源型逆变器，v_pa、v_pb、v_pc为逆变器交流侧三相电压；U_pdc为直流侧电压；L_p为滤波电感，C_p为直流电容。柔直整流器为常规的三相桥式两电平电压源型整流器，v_ra、v_rb、v_rc为整流器交流侧三相电压；U_rdc为直流侧电压；C_r为直流电容；L_r为滤波电感。u_a、u_b、u_c，i_a、i_b、i_c分别为接口N的三相电压和电流。

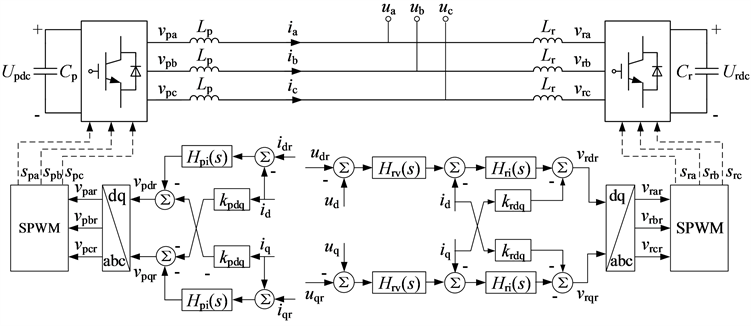
Figure 2. Equivalent circuit and control diagram of the PV and VSC-HVDC interconnection system

图2. 光伏与柔直互联系统等效电路和控制结构图

为了保证图1所示系统的稳定运行，光伏电站的控制系统需要和柔直的控制系统相互配合。光伏逆变器的控制使光伏发电系统时刻运行在最大功率点并保持单位功率因数运行 [11]，其控制由功率外环、电流内环以及锁相环(Phase Locked Loop, PLL)组成。由于功率外环的带宽较窄，在阻抗建模过程中可以忽略，因此图2中仅示出电流内环。控制结构图中， $H_{\text{pi}}\left(s\right)=k_{\text{pp}}+k_{\text{pi}}/s$ 为电流内环PI环节传递函数；k_pdq为dq轴交叉解耦系数；i_dr、i_qr，i_d、i_q分别为接口电流dq轴分量的参考值和实测值；v_par、v_pbr、v_pcr，v_pdr、v_pqr分别为交流侧电压三相参考值和dq轴分量参考值；S_pa、S_pb、S_pc为逆变器的触发信号。柔直整流器采用定交流电压控制，建立光伏电站并网所需要的交流电压，其控制由交流电压外环和电流内环组成。控制结构图中， $H_{\text{rv}}\left(s\right)=k_{\text{rvp}}+k_{\text{rvi}}/s$ 为交流电压外环PI环节传递函数； $H_{\text{ri}}\left(\text{s}\right)=k_{\text{rip}}+k_{\text{rii}}/s$ 为电流内环PI环节传递函数；k_rdq为电流内环dq轴交叉解耦系数；u_dr、u_qr，u_d、u_q分别为接口电压dq轴分量的参考值和实测值；v_rar、v_rbr、v_rcr，v_rdr、v_rqr分别为整流器交流侧电压三相参考值和dq轴分量参考值；S_ra、S_rb、S_rc为整流器的触发信号。

3. 阻抗建模

为了研究光伏与柔直互联系统的稳定性，可以采用基于阻抗的稳定性分析方法，该方法的基本思路是将待研系统划分为电源和负载两个子系统，利用源子系统与负载子系统的阻抗比去判断系统的稳定性 [12] [13]。鉴于柔直中整流器和逆变器的控制相互独立，同时计及直流电容的稳压作用，在光伏与柔直互联系统稳定运行时，本文忽略柔直逆变器对接口N电压和电流的影响，只考虑光伏逆变器和柔直整流器交互作用的影响。

接下来利用谐波线性化方法分别建立光伏逆变器和柔直整流器的阻抗模型，建模的思路为：假设接口N电压中含有正负序小信号电压谐波，通过系统的电压方程、控制过程和稳态工作点建立小信号电压谐波和小信号电流谐波的关系，从而得到系统的正负序阻抗模型。另外本文假设待研系统运行在平衡工况下，即系统的正负序阻抗解耦。

光伏逆变器在频域下的电压方程为

$V_{\text{pa}}\left(s\right)=s{L}_{\text{p}}{I}_{\text{a}}\left(s\right)+U_{\text{a}}\left(s\right)$ (1)

假设接口电压对称且含有正负序小信号谐波，则接口N的a相电压和电流的时域表达式为

$u_{\text{a}}\left(t\right)=U_{\text{1m}}\cos \left({\omega }_{1}t\right)+U_{+\text{m}}\cos \left({\omega }_{\text{+}}t+{\phi }_{\text{u}+}\right)+U_{-\text{m}}\cos \left({\omega }_{-}t+{\phi }_{\text{u}-}\right)$ (2)

$i_{\text{a}}\left(t\right)=I_{\text{1m}}\cos \left({\omega }_{1}t+{\phi }_{\text{i1}}\right)+I_{+\text{m}}\cos \left({\omega }_{+}t+{\phi }_{\text{i}+}\right)+I_{-\text{m}}\cos \left({\omega }_{-}t+{\phi }_{\text{i}-}\right)$ (3)

式中，U_1m、U_+m、U_−m，I_1m、I_+m、I_−m分别为接口电压和电流基波以及正负序谐波幅值，且U_+m和U_−m远小于U_1m，I_+m和I_-m远小于I_1m；ω₁、ω₊、ω₋分别为基波和正负序谐波角频率；φ_u+、φ_u−为接口电压正负序谐波初相位；φ_i1、φ_i+、φ_i−为电流基波以及正负序谐波初相位。

接口电压和电流经过傅里叶变换得到其频域表达式为

$U_{\text{a}}\left(\omega \right)=\{\begin{array}{l}\frac{1}{2}{U}_{\text{1m}}=U_{\text{1}}\text{,}\omega =\pm {\omega }_1\\ \frac{1}{2}{U}_{+\text{m}}{\text{e}}^{\pm \text{j}{\phi }_{\text{u}+}}=U_{\text{+}}\text{,}\omega =\pm {\omega }_{+}\\ \frac{1}{2}{U}_{-\text{m}}{\text{e}}^{\pm \text{j}{\phi }_{\text{u}-}}=U_{-}\text{,}\omega =\pm {\omega }_{-}\end{array}$ (4)

$I_{\text{a}}\left(\omega \right)=\{\begin{array}{l}\frac{1}{2}{I}_{\text{1m}}{\text{e}}^{\pm \text{j}{\phi }_{\text{i1}}}=I_{\text{1}},\omega =\pm {\omega }_1\\ \frac{1}{2}{I}_{+\text{m}}{\text{e}}^{\pm \text{j}{\phi }_{\text{i}+}}=I_{+},\omega =\pm {\omega }_{+}\\ \frac{1}{2}{I}_{-\text{m}}{\text{e}}^{\pm \text{j}{\phi }_{\text{i}-}}=I_{-},\omega =\pm {\omega }_{-}\end{array}$ (5)

考虑PLL动态特性，将接口电流变换到dq坐标系，得

$I_{\text{d}}\left(\omega \right)=\{\begin{array}{l}{I}_{\text{1m}}\cos {\phi }_{\text{i1}}\text{,}\omega =0\\ I_{\text{+}}\mp \text{j}{I}_{\text{1m}}\sin {\phi }_{\text{i1}}{T}_{\text{PLL}}\left(s\right)U_{+}\text{,}\omega =\pm \left({\omega }_{+}-{\omega }_{\text{1}}\right)\\ I_{-}\pm \text{j}{I}_{\text{1m}}\sin {\phi }_{\text{i1}}{T}_{\text{PLL}}\left(s\right)U_{-}\text{,}\omega =\pm \left({\omega }_{-}+{\omega }_{\text{1}}\right)\end{array}$ (6)

$I_{\text{q}}\left(\omega \right)=\{\begin{array}{l}{I}_{\text{1m}}\sin {\phi }_{\text{i1}}\text{,}\omega =0\\ \mp \text{j}{I}_{\text{+}}\pm \text{j}{I}_{\text{1m}}\cos {\phi }_{\text{i1}}{T}_{\text{PLL}}\left(s\right)U_{+}\text{,}\omega =\pm \left({\omega }_{+}-{\omega }_{\text{1}}\right)\\ \pm \text{j}{I}_{-}\mp \text{j}{I}_{\text{1m}}\cos {\phi }_{\text{i1}}{T}_{\text{PLL}}\left(s\right)U_{-}\text{,}\omega =\pm \left({\omega }_{-}+{\omega }_{\text{1}}\right)\end{array}$ (7)

式中， $T_{\text{PLL}}\left(s\right)=H\left(s\right)/\left[s+U_{1\text{m}}H\left(s\right)\right]$ 为谐波线性化后PLL输出相位偏差与电压谐波之间的传递函数， $H\left(s\right)=k_{\text{p}}+k_{\text{i}}/s$ 为PLL的PI环节传递函数 [14]。

由控制过程和Park反变换可得光伏逆变器交流侧a相电压的频域形式为

$V_{\text{pa}}(\omega )=\{\begin{array}{l}{U}_{\text{1}}\pm \text{j}{k}_{\text{pdq}}{I}_1\text{,}\omega =\pm {\omega }_{\text{1}}\\ -\left[H_{\text{pi}}\left(s\mp \text{j}{\omega }_{\text{1}}\right)\mp \text{j}{k}_{\text{pdq}}\right]I_{+}+T_{\text{PLL}}\left(s\mp \text{j}{\omega }_{\text{1}}\right)U_{+}\left[H_{\text{pi}}\left(s\mp \text{j}{\omega }_{\text{1}}\right)I_{\text{1}}+U_{\text{1}}\right]\text{,}\omega =\pm {\omega }_{\text{+}}\\ -\left[H_{\text{pi}}\left(s\pm \text{j}{\omega }_{\text{1}}\right)\pm \text{j}{k}_{\text{pdq}}\right]I_{-}+T_{\text{PLL}}\left(s\pm \text{j}{\omega }_{\text{1}}\right)U_{-}\left[H_{\text{pi}}\left(s\pm \text{j}{\omega }_{\text{1}}\right)I_1^{\ast }+U_{\text{1}}\right]\text{,}\omega =\pm {\omega }_{-}\end{array}$ (8)

将上式代入式(1)可得光伏逆变器的正负序阻抗分别为

$\{\begin{array}{l}{Z}_{\text{p\_p}}\left(s\right)=\frac{s{L}_{\text{p}}+H_{\text{pi}}\left(s\mp \text{j}{\omega }_{\text{1}}\right)\mp \text{j}{k}_{\text{pdq}}}{1-T_{\text{PLL}}\left(s\mp \text{j}{\omega }_{\text{1}}\right)\left[H_{\text{pi}}\left(s\mp \text{j}{\omega }_{\text{1}}\right)I_{\text{1}}+U_{\text{1}}\right]}\\ Z_{\text{p\_n}}\left(s\right)=\frac{s{L}_{\text{p}}+H_{\text{pi}}\left(s\pm \text{j}{\omega }_{\text{1}}\right)\pm \text{j}{k}_{\text{pdq}}}{1-T_{\text{PLL}}\left(s\pm \text{j}{\omega }_{\text{1}}\right)\left[H_{\text{pi}}\left(s\pm \text{j}{\omega }_{\text{1}}\right)I_{\text{1}}^{*}+U_{\text{1}}\right]}\end{array}$ (9)

按照同样的推导方法可以得到柔直整流器的正负序阻抗分别为

$\{\begin{array}{l}{Z}_{\text{r\_p}}\left(s\right)=\frac{s{L}_{\text{r}}+H_{\text{ri}}\left(s\mp \text{j}{\omega }_{\text{1}}\right)\mp \text{j}{k}_{\text{rdq}}}{1+H_{\text{rv}}\left(s\mp \text{j}{\omega }_{\text{1}}\right)H_{\text{ri}}\left(s\mp \text{j}{\omega }_{\text{1}}\right)}\\ Z_{\text{r\_n}}\left(s\right)=\frac{s{L}_{\text{r}}+H_{\text{ri}}\left(s\pm \text{j}{\omega }_{\text{1}}\right)\pm \text{j}{k}_{\text{rdq}}}{1+H_{\text{rv}}\left(s\pm \text{j}{\omega }_{\text{1}}\right)H_{\text{ri}}\left(s\pm \text{j}{\omega }_{\text{1}}\right)}\end{array}$ (10)

对比式(9)和式(10)可知，光伏逆变器的阻抗特性与电路参数、控制参数、锁相环参数以及稳态工作点有关，而柔直整流器的阻抗特性只与电路参数和控制参数有关。

4. 稳定性分析

由式(9)和式(10)可知，光伏逆变器的阻抗Z_p(s)和柔直整流器的阻抗Z_r(s)均具有LC特性，因此在一定控制参数和稳态工作点下，若在某些频段两者的阻抗模值接近且辐角相差180˚，则系统可能在该频段下发生电气谐振，导致接口电压和电流不稳定。由基于阻抗的奈奎斯特稳定判据可知，当光伏逆变器和柔直整流器都能单独稳定运行时，光伏与柔直互联系统的稳定性取决于Z_r(s)/Z_p(s)，当Z_r(s)/Z_p(s)的奈奎斯特曲线不包围(−1, j0)点时该系统稳定。

为了验证本文建立的阻抗模型用于分析光伏与柔直互联系统稳定性的有效性，基于表1的数据和文献 [15]、 [16] 的方法在PSCAD/EMTDC中建立图1所示的算例系统，其中光伏逆变器采用典型集中式逆变器参数，柔直采用上海南汇柔性直流输电工程参数。鉴于同一光伏电站中的逆变器运行特性相似，故可把所有逆变器等效为1台。测试结果证明，本文搭建的算例系统能够准确地反映光伏与柔直互联系统的运行特性，可以以此为基础进行稳定性分析。

假设光伏与柔直互联系统工作在额定状态，将Z_p(s)和Z_r(s)画在同一个bode图中如图3所示，图中M和A分别表示阻抗的模值和辐角，f表示频率。由图3可知，光伏逆变器与柔直整流器的负序阻抗特性相近，而正序阻抗特性在基频附近存在较大差异。柔直整流器在基频附近的正序阻抗模值较小且关于50 Hz对称，正序阻抗辐角在50 Hz处中心对称，发生了从容性到感性的骤变。光伏逆变器正序阻抗模值在基频附近较大且关于50 Hz对称，正序阻抗辐角在50 Hz处中心对称，发生了从感性到容性的骤变。

Table 1. Parameters of the example system

表1. 算例系统参数

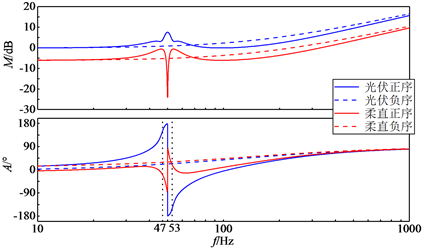
Figure 3. Impedance of PV inverter and VSC-HVDC rectifier

图3. 光伏逆变器和柔直整流器阻抗

从图3还可以看出，光伏逆变器和柔直整流器的正序阻抗在47 Hz和53 Hz处模值接近且辐角相差180˚，存在谐振的可能性，而两者的负序阻抗虽然模值接近，但辐角不满足谐振条件，因此系统的稳定性取决于两者正序阻抗的相互作用，鉴于此，后文只研究正序阻抗引起的稳定性问题。图4示出了Z_r(s)/Z_p(s)的奈奎斯特曲线，曲线表明，在现有条件下算例系统稳定运行，但在47 Hz和53 Hz处有发生谐振的可能性。

Figure 4. Nyquist curve of Z_r(s)/Z_p(s)

图4. Z_r(s)/Z_p(s)的奈奎斯特曲线

图5示出了算例系统暂态过程结束后接口电压和电流的仿真波形以及接口电流的频谱图。由图可知，接口电压和电流明显畸变，接口电流在47 Hz和53 Hz处发生了振荡，两个频率处的振荡幅值相等，这与理论分析的结果一致。额定运行状态下47 Hz和53 Hz处的单次谐波含有率均达到了40.48%。由此可知，利用本文建立的阻抗模型，可以判断光伏与柔直互联系统的稳定性，并能准确定位接口电压和电流的振荡频率。

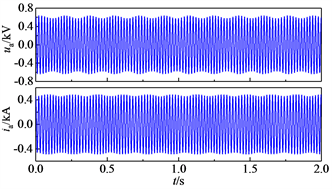(a) 接口电压和电流波形 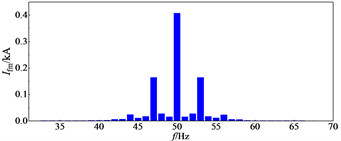(b) 接口电流频谱

Figure 5. Simulation results under rated operation condition

图5. 额定运行状态下的仿真结果

5. 稳定性影响因素分析

本节将利用基于阻抗的奈奎斯特稳定判据分析光伏电站输出功率、柔直整流器控制参数以及PLL参数对系统稳定性的影响。

由式(9)可知，当光伏电站的输出功率改变，亦即光伏逆变器输出电流改变时，光伏逆变器的阻抗特性也会发生改变。图6(a)示出了光伏电站输出功率为额定功率的60%、80%和100%时Z_r(s)/Z_p(s)的奈奎斯特曲线。曲线表明，随着光伏电站输出功率的增加，奈奎斯特曲线逐渐靠近(−1, j0)点，系统的稳定性降低。当光伏电站发出额定功率时，光伏逆变器的阻抗是确定的，为了在此种情况下给系统设置足够的稳定裕度，需要调节柔直整流器的阻抗，使Z_r(s)/Z_p(s)的奈奎斯特曲线尽可能远离(−1, j0)点。

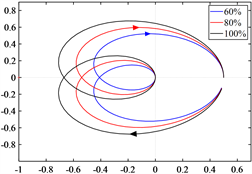(a) 光伏电站输出功率的影响 (b) k_rvp的影响 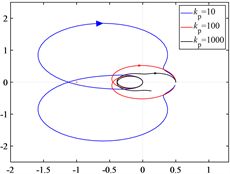(c) k_p的影响

Figure 6. Nyquist curve of Z_r(s)/Z_p(s) with different parameters

图6. 不同参数下Z_r(s)/Z_p(s)的奈奎斯特曲线

柔直整流器的作用是建立交流电压，为光伏逆变器提供参考电压，因此其外环电压控制对接口电压和电流的稳定性有重大影响。由式(10)可知，H_rv(s)的增大可有效减小柔直整流器阻抗的模值，当柔直整流器阻抗模值减小到一定程度时，可破坏谐振条件，使接口电压和电流的稳定性增强。同样，H_rv(s)的减小可使柔直整流站阻抗的模值增大，也可以破坏谐振条件，但H_rv(s)的减小会降低外环电压控制的响应速度，因此不适宜采用减小H_rv(s)的方法去提高接口电压和电流的稳定性。保持其他参数不变，画出k_rvp分别为0.5、1、1.5时Z_r(s)/Z_p(s)的奈奎斯特曲线如图6(b)所示。由图可知，当k_rvp取0.5时，奈奎斯特曲线包围(−1, j0)点，系统不稳定，随着k_rvp的增大，奈奎斯特曲线逐渐远离(−1, j0)点，系统稳定运行且稳定裕度增加。图7示出了其他数据不变而k_rvp = 1.5时的仿真结果，和图5中k_rvp = 1时的情况相比，接口电压和电流畸变较小，系统的稳定性明显提高，这证明适当增大柔直整流器外环电压控制PI环节的比例系数可以提高系统的稳定性。

(a) 接口电压和电流波形 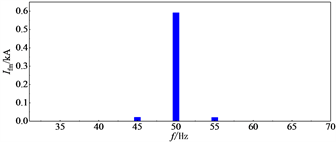(b) 接口电流频谱

Figure 7. Simulation results when k_rvp = 1.5

图7. k_rvp = 1.5时仿真结果

光伏逆变器需要利用PLL去检测交流电压的实时相位，交流电压畸变会使PLL输出相位产生偏差，由式(9)可知T_PLL(s)会影响光伏逆变器的阻抗特性，进而影响系统的稳定性。保持其他参数不变，画出k_p分别为10、100和1000时光伏逆变器正序阻抗特性曲线如图8所示。由图可知，随着k_p的增大，光伏逆变器阻抗的模值增大，k_p对阻抗特性的影响范围也向基频两侧拓展，因此振荡的频率可能会向50 Hz两侧更远的方向移动，但振荡的幅值会减小。

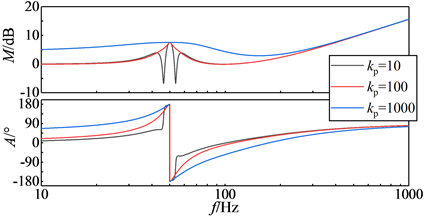
Figure 8. Influence of k_p on the impedance of PV inverter

图8. k_p对光伏逆变器阻抗的影响

k_p = 200时的仿真结果显示，接口电流中含有45 Hz和55 Hz的振荡分量，单次谐波含有率均为2.47%，和图5中k_p = 50的情况相比，振荡频率向50 Hz两侧发生了移动，振荡幅值明显减小。保持其他参数不变，画出k_p分别为10、100和1000时Z_r(s)/Z_p(s)的奈奎斯特曲线如图6(c)所示。由图可知，当k_p取10时，奈奎斯特曲线包围(−1, j0)点，系统不稳定，随着k_p的增大，奈奎斯特曲线逐渐远离(−1, j0)点，系统稳定运行且稳定裕度增加。

6. 结论

本文利用谐波线性化方法建立了光伏与柔直互联系统的阻抗模型，分析了光伏电站与柔直整流站接口发生振荡的机理和影响光伏与柔直互联系统稳定性的因素。主要结论如下：

(1) 光伏逆变器和柔直整流器阻抗具有LC特性，两者会在某些频段下发生电气谐振，而使接口电压和电流产生振荡，振荡频率关于50 Hz对称且振荡幅值相等。

(2) 随着光伏电站输出功率的增加，光伏与柔直互联系统的稳定性降低。

(3) 增大柔直整流器外环电压控制的比例系数可以减小柔直整流器阻抗模值，破坏谐振条件，提高系统的稳定性。

(4) 增大光伏逆变器PLL比例系数会使振荡频率向50 Hz两侧移动，并有效减小振荡幅值，提高系统的稳定性。

基金项目

国家重点研发计划智能电网技术与装备重点专项(2016YFB0900600)。