1. 引言
近年来,我国物流业的增速持续放缓,物流成本持续位于高位,2019年受新冠疫情影响物流业首当其冲。与此同时,传统产品在市场价格竞争中尽力压缩成本,使得处于劣势地位的物流企业被迫减少盈利,这也增加了行业治理和市场调理的难度。《中华人民共和国国民经济和社会发展第十三个五年规划纲要》强调了要着力供给侧结构性改革并着重提升供给体系的质量和效率。物流、资金流、商流和信息流等的高效配置组成了供给侧改革的中心工作之一,而物流则是衔接供应端和需求侧的重要因素。因而,物流业不仅是基础性产业,还是供给侧改革的重要对象和内容。
近年来,随着互联网经济的发展及世界各国联系的逐步加深,现代物流作为“第三利润源泉”,在城市经济发展中的价值逐步凸显,其产业规模和需求层次也已成为衡量区域综合实力的关键指标。从德国等发达国家的经验来看,物流需求是经济发展的引致需要,经济发展水平和产业布局一定程度上决定其产业规模和结构形式。
常州市位于长三角的核心地带,也是较为发达的制造业中心,对江苏及长江经济带发展起着重要的作用。同时,摆脱了传统自给自足的小农经济之后,较为丰富的农产品给常州带来了快速发展的农业经济。特别是苏南经济模式,更是全国范围内很早实现工业化的发展模式,造就了一批规模化制造业企业。如牛仔布料行业领先的黑牡丹(集团)股份有限公司、火车零部件制造企业的中坚力量中国南车集团戚墅堰机车车辆厂、集农业装备和冷用器材制造的常发集团等业内领先的制造业企业。
常州区位靠近上海,交通四通八达,与苏州、无锡联系密切,形成苏锡常城市圈。目前,常州有8条高速穿城,市内交通有环城高架道路、机场快速道路和1、2号地铁线路,已成为所有区县都有高速通过的城市。苏南将形成地铁城市圈——交通极为便利,更适宜商业社会发展。这些优势无疑大大促进了常州城市经济的整体发展,在这个过程中物流业也发挥着重要的作用。然而,研究也发现,尽管随着城市经济的快速发展,常州市物流业竞争力也得到了长足的提升,但是在短期内,许多物流企业大多仍旧沿袭着传统发展方式,采取家族式管理,这在一定程度上抑制了企业规模的扩大、管理水平和竞争力的提升等。因此,在供给侧改革背景下开展常州现代物流业竞争力研究无疑具有重要的理论价值和实际应用价值。
2. 文献综述
由于城市物流与城市经济的发展息息相关,因此近年来许多的专家学者对此展开了较为深入系统的研究。在对其研究过程中,学者们普遍认为城市的政策、产业结构、企业主体、区域经济活力、物流人才、产品服务结构、供应链结构、物流的基础设施设备等都会影响这座城市或该区域的物流业竞争力。
在物流效率研究方面,国内学者田刚、李南(2009)借助超越对数随机前沿模型对各地区物流业全要素生产率的增长情况做了详细研究后发现各地区的物流业发展水平目前存在很大差异,转变经济发展模式和物流业发展模式迫在眉睫 [1];乐小兵、王瑛(2014)构造了区域物流效率评价指标体系,并借助DEA效率评价模型对广西省物流系统的有效性和效率进行了分析。基于相关的面板数据,借助生产前沿模型估算供给侧结构性改革在物流行业的作用空间,进而对物流技术效率进行收敛性研究,并基于物流技术效率的影响因素为物流业的转型提供方向 [2]。
在城市物流规划及物流系统优化研究方面,段华薇、严余松(2014)认为城市物流系统的发展不仅需要系统规划,还需要基于预测物流产业的需求及发展现状对基础设施进行阐明 [3]。基于物流系统理论,吴娜、杨晓艳(2013)认为供需市场是物流主体,应由此来确定城市物流系统体系框架的设计方法和步骤并建立其框架,从而探究城市物流受城市供应侧和需求侧关系的影响 [4]。而为了在保护环境基础上提高经济发展效益,就紧急情况下应急物资的配送问题,刘斌、马祖军(2014)认为,在考虑应急物质资源需求量和种类多样化情况下,应综合使用不同的运输方式,建立多阶段分层算法模型,借助路径配送优化和优化选址,从而实现成本低、配送时间较短的目的 [5]。刘学林、马俊,张雅蕊(2014)则基于系统工程理论,以襄阳市物流系统为研究对象,认为物流工程的建设须考虑产业结构特点、城市经济发展等因素,并借助科学规划建立高效便捷的物流信息平台,从而完善该市物流系统 [6]。
在区域竞争力研究方面,刘玉美(2013)认为提升区域的物流竞争力的方式包括加速培养物流人才、制造轻松的企业氛围、强调物流基础设施的建设、构建信息平台并实现物流作业规模化 [7]。席建国(2014)基于构建的城市物流竞争力的评估指标体系,通过面板数据检验了指标间的关系,并借助单纯前向神经网络的非线性主成分分析方法,以海峡西岸经济区的城市物流竞争力为例,进行了实证研究 [8]。贾冀南(2015)等通过建立城市物流竞争力的指标评价体系,借助直觉模糊层次分析法综合评价了城市的物流业竞争力,并结合实证分析的结果验证直觉模糊层次分析法在该领域的实际应用意义 [9]。司文峰(2015)以环长株潭城市群及武汉城市圈为研究对象建立物流竞争力的评价体系,借助因子分析法,结合数据动态比较其物流竞争力,以聚类分析为基础阐明城市群物流发展的层级水平,并为提升其物流竞争力给出建议 [10]。陈文新、刘冬、孙善祥(2016)通过建立地理加权空间计量模型,对我国各省物流发展水平的收敛性进行分析,结果表明现阶段的物流发展水平的空间差异还比较显著,其平均收敛速度在空间上的聚集效应还较为明显,并根据研究给出了加快区域物流一体化的部分建议 [11]。孙庆兰、陈浩行(2016)基于城市物流产业竞争力的评价指标体系,根据“一带一路”中6座节点城市的相关物流数据,并结合综合评价指数法和熵权法,借助Esl指数,综合评价并比较各城市的物流竞争力 [12]。
在区域物流与区域经济研究方面,贾海成(2012)以天津和上海为例分析不同城市物流发展的特点,鼓励扩大产业规模并加快物流资源的跨区域的流动,从而提高物流效益,并证明不同地区的经济发展和物流业发展之间存在并不相同的互动效应 [13]。张广胜(2013)借助主成分聚类分析法对内陆城市物流发展水平较低的现象进行分析,发现区域物流和区域经济之间存在着协整关系。此外,区域经济增长可以促进物流业的发展,但区域物流对于区域经济的增长影响并不明显 [14]。刘俊华、李瑶琴(2013)认为,区域物流的资源整合须以中心城市为核心,并有机结合区域内的物流点、线、网络等资源,从而增高资源的利用效率 [15]。基于数据包络分析,廖志高、许明辉(2014)构建了经济发展水平和物流的系统动力学模型,借助DEA模型定量分析松弛变量和影响因素的关系,发现物流发展能够促进城市经济增长 [16]。
关于推动物流业的供给侧改革,何黎明(2016)建议坚持效果为导向,关注主要矛盾,转变物流业发展模式,提高物流服务的质量和效率,从而满足经济发展对物流业发展的要求 [17]。史锦梅(2016)认为,物流设施的标准化和现代化等将加速物流业的转型。此外,政府办事效率的提高以及物流人才培育方式的创新将加速物流业的供给侧改革 [18]。
从以上综述可以看出,近年来学者们对城市物流竞争力展开了较为深入的研究。但就其研究对象来看,研究多以省级行政区域作为研究对象,而较少考虑将一个城市作为研究对象。就其研究方法来看,目前许多专家学者从不同的研究目的和角度出发采用了多种不同的研究方法。本文考虑到城市物流竞争力系统是一个具有组织耗散结构性质的开放系统,是具备多反馈环、非单一变量的高阶非线性反馈系统。这类系统普遍存在突现性、复杂性、动态性、延迟性等动力学性质,因此更适合采用系统动力学的方法开展研究。因此,本文将在供给侧改革背景下构建常州现代物流业竞争力系统动力学模型;运用系统系统动力学的方法从宏观上探讨各个构成要素之间的关系,研究各要素对城市物流竞争力的影响程度;并使用VENSIM软件建模以对系统进行模拟仿真分析,从而在供给侧改革背景下预测常州市现代物流业竞争力的发展趋势;在此基础上,对于如何提升常州市现代物流业竞争力提出相应的对策和建议。
3. 常州市现代物流业竞争力系统动力学模型构成要素
3.1. 城市现代物流业竞争力系统及子系统分析
针对常州市现代物流业现状,结合相关专家学者的研究成果和“供给侧改革”的背景,本文将常州市现代物流业竞争力系统划分为六个子模块,分别是城市经济发展子系统、物流供给与需求子系统、城市就业人口子系统、科技创新子系统、生态环境子系统、物流产业规模子系统。
3.1.1. 城市经济发展子系统
城市现代物流业的发展与城市经济发展水平密切相关。城市的GDP是衡量一座城市经济发展水平的核心指标,其增长与城市的物流发展水平是正相关关系。城市经济发展将促进对物流固定资产的投资,从而促进城市现代物流业的发展;而作为城市经济发展粘合剂的物流业的发展也会促进城市经济的快速发展。
考虑到物流需求与供给能力的差额会阻碍城市的经济发展,因此本文借用“物流积压”指标来衡量其对城市经济的阻碍。
3.1.2. 物流供给与需求子系统
城市现代物流业的供给与需求在城市现代物流业竞争力系统中居于重要地位。通常物流供给与需求的关系存在三种状态,即物流供给等于需求、物流供给大于需求、物流供给小于需求。本文认为物流供给略大于需求较适合促进城市的经济发展。因为,物流供给能力在一定程度上可以促进物流需求的数量及质量的提升。
本文选取技术创新及物流产业资本提供的物流供给能力和物流效率影响因子描述城市的物流供给能力。创新水平的提高、产业资本及投资与物流效率的提升都将促进城市物流供给能力的提升。
3.1.3. 城市就业人口子系统
城市的发展离不开城市就业人口的辛勤努力,城市就业人口一定程度也体现了城市的发展规模。
本文选取城市GDP增长系数、生态环境对就业人口影响因子、城市GDP对城市就业人口影响系数等指标描述城市就业人口。城市经济发展水平的提升和生态环境的改善都会促进城市就业人口增长。
3.1.4. 科技创新子系统
科技创新水平体现了城市未来发展的潜力。供给侧结构性改革背景下,万众创新的思想深入人心。科技水平的提高将有利于城市现代物流业实现社会化、专业化、信息化。
本文选用城市专利授权量衡量城市的创新技术水平。城市专利授权量越多,创新技术水平也越高,因此城市物流供给能力也得到提升。
3.1.5. 生态环境子系统
随着生活水平和教育水平提升,人们开始关注自己生活周边的生态环境质量。政府对于物流固定资产的投资(包括城市地下水道及公共交通)和对园林绿化的投入对生态环境改善是正相关的。绿地建设投入越多,城市未来的生态环境越好。
本文选用城市空气质量达到及好于二级的天数描述城市生态环境。政府对园林绿地面积的建设投入和物流固定资产投资将促进生态环境改善,优美的生态环境将吸引更多高层次的人才进入,从而在一定程度上促进城市经济的发展。
3.1.6. 物流产业规模子系统
政府对于物流产业的固定资产投资能促进公共交通和物流企业的发展,然而由于物流设备自身折旧、管理或使用不当等会造成物流产业资本自身的消耗。而且物流产业资本将会转化为产业的最大供给能力,从而构成物流供给能力的一部分。
在物流产业规模子系统中,本文选用了城市物流固定资产投资的延迟值作为指标,通过物流产业资本增加量与物流产业资本消耗的差值来衡量城市物流产业规模。现实中,小规模物流企业大多缺乏事中事后监管,行业内的集约化发展困难重重。通过技术和管理等手段减少资本消耗,在有限的物流固定资产投资的情况下,仍旧可以提升物流供给能力。
3.2. 常州市现代物流业竞争力分析
3.2.1. 常州市现代物流业竞争力模型的系统边界
通过查阅文献并结合常州城市的实际情况,本文确定的系统边界如表1所示。
资料来源:本文整理。
3.2.2. 常州市现代物流业竞争力因果关系分析
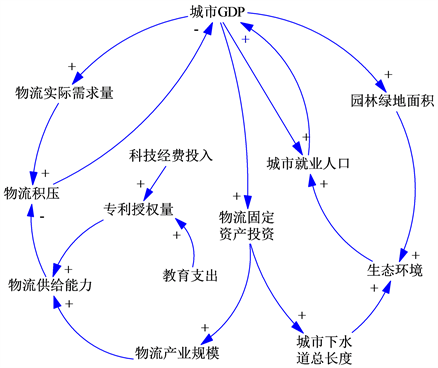
确立系统动力学的反馈机制是该研究的重点。通过对系统中各因素之间的因果关系、子系统与系统之间整体和部分的关系研究,在确立的系统边界基础上把其因果关系连成反馈环路。根据对供给侧结构性改革背景下常州市现代物流业竞争力系统及其子系统的分析,基于设置的系统边界,可以确定其因果关系如图1所示。
 资料来源:本文整理绘制。
资料来源:本文整理绘制。
Figure 1. Causal relationship
图1. 因果关系图
图1包含4个反馈回路,如图2(a)~(d)所示。其中,图2(a)为城市GDP与物流积压的负反馈回路,城市经济发展水平的提高促进城市物流实际需求量提高,当物流实际需求量超过物流供给能力造成的物流积压增加,将对城市经济的发展造成阻碍;图2(b)为城市GDP与物流产业规模之间的正反馈环路,城市经济发展加大对物流固定资产投资,一段时间的滞后转变为物流产业规模,从而增大了城市的物流供给能力,减少了物流积压,间接地促进城市经济发展。图2(c)为城市GDP同生态环境的正反馈环,城市GDP增长带动对园林绿地的投资,改善了生态环境,优美宜人的生态环境又将吸引更多高层次人才,一定程度上促进了城市经济的发展。图2(d)为物流固定资产投资与生态环境的正反馈环,城市经济增长与物流固定资产投资正相关,城市下水道和公共交通的投资建设有利于城市生态环境的改善,优美宜人的城市环境吸引更多高层次人才,促进城市经济进一步发展。
 (a)
(a) 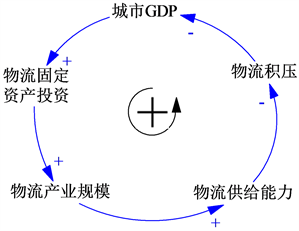 (b)
(b) 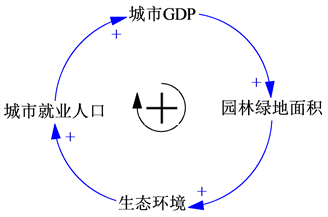 (c)
(c)  (d)资料来源:本文整理绘制。
(d)资料来源:本文整理绘制。
Figure 2. Basic feedback-loop of Urban Logistics Competitiveness System
图2. 城市现代物流业竞争力系统基本反馈环
4. 常州市现代物流业竞争力系统动力学模型
4.1. 构建常州市现代物流业竞争力模型系统流图
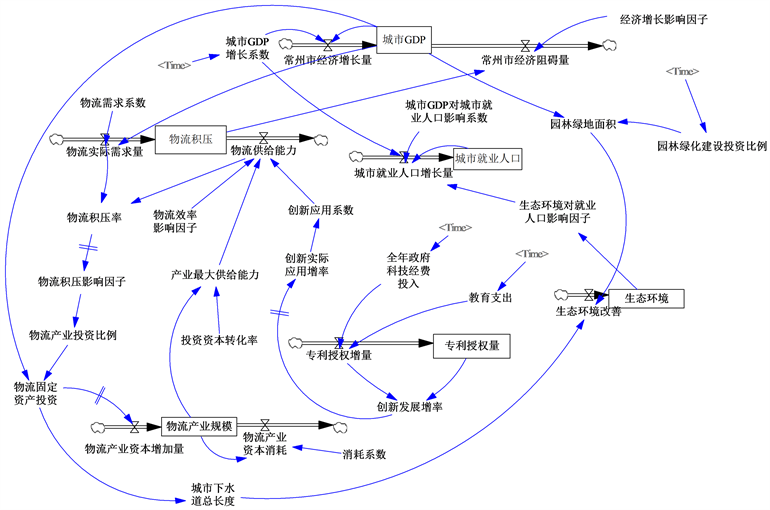
供给侧结构性改革背景下常州市现代物流业竞争力系统是一个具有自组织耗散结构性质的开放体系,具有非单一变量、多回路的高阶非线性反馈系统,具有复杂性、动态性、延迟性、突现性、抽象性等动力学特性。系统动力学以定量描述为主,辅以半定量、半定性或定性描述,并结合定量模型与概念模型。本文基于绘制的因果反馈环路,利用系统动力学描述各种变量及其相互关系的特有符号绘成流图,如图3所示。
 资料来源:本文整理绘制。
资料来源:本文整理绘制。
Figure 3. System flow of Changzhou modern logistics industry competitiveness model
图3. 常州市现代物流业竞争力模型系统流图
4.2. 常州市现代物流业竞争力模型变量说明
系统动力学模型中的变量共有四种(见图3所示),分别是状态变量,用L表示;速率变量,用R表示;辅助变量,用A表示;常量,用C表示。各变量的类型、定义及单位如表2所示。


Table 2. Variable description of Changzhou modern logistics industry competitiveness model
表2. 常州市现代物流业竞争力模型变量说明
资料来源:本文整理。
4.3. 常州市现代物流业竞争力模型参数估计
本文中除了一些具有明显相关性的变量外,还存在一些没有特定数量规律的非线性的变量,对于这样的变量,本文选择使用表函数的方法进行确定;对于一些有固定公式的变量,本文直接选取该公式;对于一些相关性较强但是没有直接数量关系的变量,本文主要借助SPSS中的回归分析,通过2006~2016年的数据得到其回归方程。
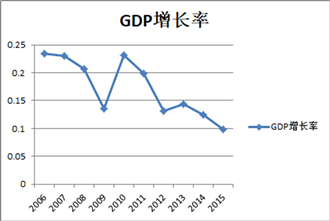
4.3.1. 城市GDP增长系数表函数
城市GDP增长系数表函数的自变量是年份,因变量是往年城市GDP增长系数。城市GDP增长系数表函数的确定如图4所示。
 资料来源:本文整理绘制。
资料来源:本文整理绘制。
Figure 4. Table function of Changzhou GDP growth coefficient
图4. 常州市GDP增长系数表函数
4.3.2. 物流产业投资比例表函数
物流产业投资比例表函数的自变量是物流积压影响因子,因变量是物流产业投资比例。物流产业投资比例表函数的确定如图5所示。
 资料来源:本文整理绘制。
资料来源:本文整理绘制。
Figure 5. Table function of Changzhou logistics industry investment proportion
图5. 常州市物流产业投资比例表函数
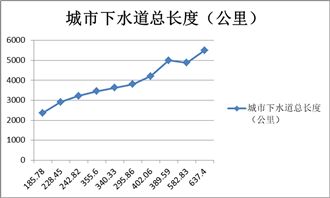
4.3.3. 城市下水道总长度
城市下水道总长度表函数的自变量是物流固定资产投资,因变量是城市下水道总长度。城市下水道总长度表函数的确定如图6所示。
 资料来源:本文整理绘制。
资料来源:本文整理绘制。
Figure 6. Table function of total length of sewer in Changzhou City
图6. 常州市下水道总长度表函数
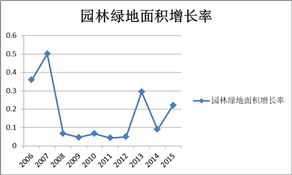
4.3.4. 园林绿化建设投资比例表函数
园林绿化建设投资比例表函数的自变量是年份,因变量是园林绿化建设投资比例。园林绿化建设投资比例表函数的确定如图7所示。
 资料来源:本文整理绘制。
资料来源:本文整理绘制。
Figure 7. Table function of Changzhou landscape construction investment proportion
图7. 常州市园林绿化建设投资比例表函数
4.3.5. 生态环境对就业人口影响因子
生态环境对就业人口影响因子表函数的自变量是生态环境,因变量是生态环境对就业人口影响因子。生态环境对就业人口影响因子表函数的确定如图8所示。
 资料来源:本文整理绘制。
资料来源:本文整理绘制。
Figure 8. Table function of Changzhou ecological environment impact on employment population
图8. 常州市生态环境对就业人口影响因子表函数
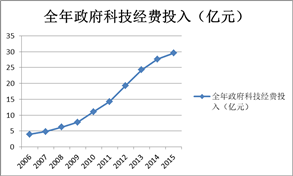
4.3.6. 全年政府科技经费投入
全年政府科技经费投入表函数的自变量是年份,因变量是全年政府科技经费投入。全年政府科技经费投入表函数的确定如图9所示。
 资料来源:本文整理绘制。
资料来源:本文整理绘制。
Figure 9. Table function of annual government science and technology investment of Changzhou City
图9. 常州市全年政府科技经费投入表函数
4.3.7. 教育支出
教育支出表函数的自变量是年份,因变量是教育支出。教育支出表函数的确定如图10所示。
 资料来源:本文整理绘制。
资料来源:本文整理绘制。
Figure 10. Table function of Changzhou education expenditure
图10. 常州市教育支出表函数
4.3.8. 生态环境改善多元回归分析
本文研究显示生态环境改善与城市下水道总长度和园林绿地面积具有较强的相关性,且空气质量达到及好于二级的天数可综合反映城市的生态环境。因此,本文通过SPSS软件对常州市城市下水道总长度和园林绿地面积来拟合常州市生态环境改善。经拟合后发现R达到81%,显著性水平为2.4%,拟合效果较好。因此,得到回归方程生态环境改善 = 0.049 * 园林绿地面积 − 0.094 * 城市下水道总长度 − 0.045。
4.3.9. 专利授权增量回归分析
城市专利授权增量同全年政府科技经费投入和教育支出有较大关联。因此,本文借助SPSS软件对全年政府科技经费投入和教育支出来拟合常州市专利授权增量和全年政府科技经费投入及教育支出的关系。经拟合后发现R达到85.7%,显著性水平为1%,拟合效果较好。因此,得回归方程专利授权增量 = 278.892 * 教育支出 − 523.733 * 全年政府科技经费投入 − 3526.36。
4.3.10. 物流积压影响因子延迟函数
现实中,城市的物流积压率对于物流产业投资比例存在延迟时间,因此借助了DELAY FIXED函数对现实情况进行模拟。
4.3.11. 创新实际应用增率延迟函数
在实际情况下,从专利授权到应用于生产实践存在时间延迟,因此也借助了DELAY FIXED函数对现实情况进行模拟。
4.3.12. 物流产业资本增加量延迟函数
在实际情况下,从投资物流固定资产转变为物流产业资本存在时间延迟,因此同样借助了DELAY FIXED函数对现实情况进行模拟。
4.3.13. 其他参数确定
通过文献研究法、估计法等方法确定其动力学模型的部分参数。然而,常州市现代物流业竞争力模型是一个较为复杂的社会经济系统,其涉及影响因素很多,因此不可避免会有难以获取的参数值。所以,本文在借助综合估计、文献研究等方法基础上,通过模型运行不断调整参数以符合实际,具体参数值见表3。
资料来源:本文整理。
4.4. 常州市现代物流业竞争力模型动力学方程
基于本文对系统中各因素之间的因果关系的分析,借助SPSS软件对常州市的历史数据进行多元回归、线性回归等,得到常州市现代物流业竞争力模型动力学方程式如下:
4.4.1. FINAL TIME=2025
Units:Year
The final time for the simulation
4.4.2. INTIAL TIME=2006
Units:Year
The initial time for the simulation
4.4.3. SAVEPER=
TIME STEP
Units:Year[0,?]
The frequency with which output is stored
4.4.4. TIME STEP=1
Units:Year[0,?]
The time step for the simulation
4.4.5.城市GDP增长系数=WITH LOOKUP
(Time,([(2006,0)-(2025,1)],(2006,0.2347),(2007,0.2302),(2008,0.2074),(2009,0.1349),(2010,0.2313),(2011,0.1991),(2012,0.1316),(2013,0.1439),(2014,0.1245),(2015,0.0987)))
4.4.6.城市GDP=INTEG(常州市经济增长量-常州市经济阻碍量,1585.11)
4.4.7.常州市经济增长量=城市GDP增长系数*城市GDP
4.4.8.常州市经济阻碍量=物流积压*经济增长影响因子
4.4.9.物流实际需求量=城市GDP*物流需求系数
4.4.10.物流积压=INTEG(物流实际需求量-物流供给能力,0)
4.4.11.物流供给能力=产业最大供给能力*物流效率影响因子*创新应用系数
4.4.12.城市就业人口增长量=城市GDP增长系数*城市GDP对城市就业人口影响系数*城市就业人口*生态环境对就业人口影响因子
4.4.13.城市就业人口=INTEG(城市就业人口增长量,225.81)
4.4.14.园林绿化建设投资比例=WITH LOOKUP
(Time([(2006,0)-(2025,1)],(2006,0.000254683),(2007,0.00031654),(2008,0.000285397),(2009,0.000268777),(2010,0.000237184),(2011,0.000210417),(2012,0.000199352),(2013,0.000181746),(2014,0.000179793),(2015,0.000204203)))
4.4.15.物流积压率=(物流实际需求量-物流供给能力)/物流实际需求量
4.4.16.园林绿地面积=园林绿化建设投资比例*城市GDP
4.4.17.创新应用系数=1+创新实际应用增率
4.4.18.生态环境对就业人口影响因子=WITH LOOKUP
(生态环境,
([(0,-0.008)-(400,10)],(222,-0.00634138),(231,0.00814651),(245,0),(314.5,0.191112),(319,1.00082),(320,0.403935),(324.5,0.770081),(325,0.561417),(327,0.300918),(330,0.254905)))
4.4.19.物流积压影响因子=DELAY FIXED(物流积压率,1,物流效率影响因子)
4.4.20.产业最大供给能力=投资资本转化率*物流产业规模
4.4.21.创新实际应用增率= DELAY FIXED(创新发展增率,1,0.25)
4.4.22.全年政府科技经费投入=WITH LOOKUP
(Time,([(2006,0)-(2025,40)],(2006,3.96),(2007,4.83),(2008,6.24),(2009,7.76),(2010,11.1025),(2011,14.3),(2012,19.33),(2013,24.3),(2014,27.6711),(2015,29.5479)))
4.4.23.教育支出=WITH LOOKUP
(Time,([(2006,0)-(2025,80)],(2006,20),(2007,24.5),(2008,27.7585),(2009,35.3),(2010,43.8073),(2011,50),(2012,66.2),(2013,66.6),(2014,68.6),(2015,76.5)))
4.4.24.生态环境改善=0.049*园林绿地面积-0.094*城市下水道总长度-0.045
4.4.25.生态环境=INTEG(生态环境改善,314.5)
4.4.26.物流产业投资比例=WITH LOOKUP
(物流积压影响因子,
([(2006,0)-(2025,1)],(2006,0.1172),(2007,0.1194),(2008,0.1071),(2009,0.1411),(2010,0.1118),(2011,0.0826),(2012,0.1013),(2013,0.0875),(2014,0.1189),(2015,0.1209))
4.4.27.专利授权增量= 278.892*教育支出-523.733*全年政府科技经费投入-3526.36
4.4.28.专利授权量=INTEG(专利授权增量,1554)
4.4.29.物流固定资产投资=城市GDP*物流产业投资比例
4.4.30.物流产业资本增加量=DELAY FIXED(物流固定资产投资,1,204.21)
4.4.31.物流产业规模=INTEG(物流产业资本增加量-物流产业资本消耗,204.21)
4.4.32.物流产业资本消耗=消耗系数*物流产业规模
4.4.33.创新发展增率=专利授权增量/专利授权量
4.4.34.城市下水道总长度=WITH LOOKUP
(物流固定资产投资,
([(0,0)-(6.37395e+006,6000)],(1.85784e+006,2366),(2.28453e+006,2918),(2.42825e+006,3223),(2.95859e+006,3807),(3.40329e+006,3627),(3.55595e+006,3458),(3.89588e+006,5003),(4.02057e+006,4214),(5.82827e+006,4876),(6.37395e+006,5503))
4.5. 供给侧改革背景下常州市现代物流业竞争力模型有效性检验
为检验模型的稳定性,本文分别使用1年、0.5年、0.25年的步长对城市GDP、专利授权量、城市就业人口、物流积压、生态环境和物流产业规模进行研究与分析。得到结果如图11(a)至图11(f)所示。
根据图11(a)至图11(f)中不同步长的稳定性检验结果可知,分别使用不同步长进行仿真,所得仿真曲线在步长为1年、步长为6个月以及步长为3个月时的趋势大致相同,仿真结果基本吻合,以此判定该模型的稳定性较好。
与此同时,考虑到本文在建立模型中,有些必要参数无法直接获得,而是通过调查和查阅相关资料,通过SPSS等分析工具处理得到的间接数据。为了保证本文模型的可信度,本文选取了相关的模拟结果同搜集的数据进行对比,检验其精确度。借助VensimPLE仿真软件进行模拟仿真。仿真结果显示,其误差均在10%内。因此,本文模型的拟合效果较为理想。
5. 常州市现代物流业竞争力模型仿真预测分析
通过《常州市统计年鉴》、《中国物流年鉴》、《常州市国民经济和社会发展统计公报》及《中国统计年鉴》等获取初始资料,并根据上述方程式及其参数的设置, 对模型运用Vensim软件进行模拟仿真和分析。
5.1. 常州市经济社会发展
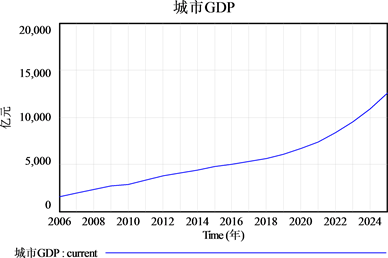
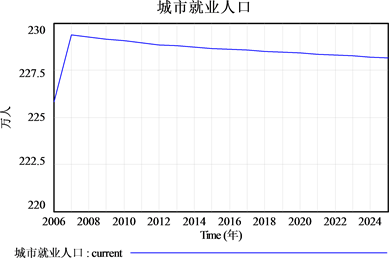
选取“城市GDP”、“城市就业人口”,输出常州市国内生产总值和常州市城市就业人口的模拟预测结果(见图12、图13)。从图中可以清楚看出,在城市就业人口趋于平缓的情况下,从2006年到2016年常州市的国内生产总值还呈现不断增长趋势,并且在未来八年里GDP仍然保持快速上涨势头。
 资料来源:本文整理绘制。
资料来源:本文整理绘制。
Figure 12. Forecast results of Changzhou GDP
图12. 常州市GDP预测结果
 资料来源:本文整理绘制。
资料来源:本文整理绘制。
Figure 13. Prediction results of employment population in Changzhou city
图13. 常州市就业人口预测结果
5.2. 生态环境
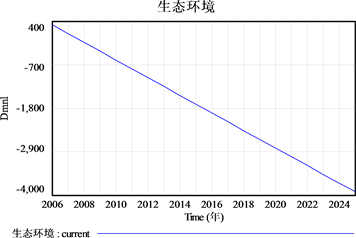
选取“生态环境”并输出仿真曲线,如图14所示。尽管近年来国家积极推进节能环保,并制定采取了一些必要措施,然而生态系统具有高度复杂、关联性,在短期内仍可能呈现不容乐观的趋势。因此,不仅大众须大力施行节能减排、低碳环保举措,政府和企业更要继续转变经济发展方式—由原来依靠原料、低劳动成本、高能耗低效率的发展方式朝着创新、高效、节能环保的可持续发展方式转变。
 资料来源:本文整理绘制。
资料来源:本文整理绘制。
Figure 14. Prediction results of ecological environment in Changzhou City
图14. 常州市生态环境预测结果
5.3. 物流产业规模
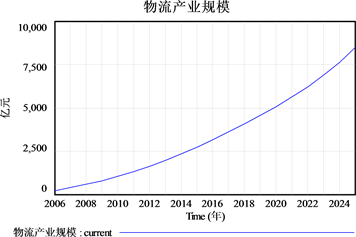
选取“物流产业规模”并输出仿真曲线,如图15所示。从图中可以清楚看出,随着城市经济的发展,社会对物流固定资产的投资也与日俱增,在未来的八年里,物流产业规模依旧保持增长势头。
 资料来源:本文整理绘制。
资料来源:本文整理绘制。
Figure 15. Prediction results of Changzhou logistics industry scale
图15. 常州市物流产业规模预测结果
5.4. 专利授权量
选取“专利授权量”并输出仿真曲线,如图16所示。从图中可以看出,从2006至2016年常州市每年的专利授权量稳步提高,在未来的八年里也将依旧不断增高。
 资料来源:本文整理绘制。
资料来源:本文整理绘制。
Figure 16. Prediction results of patent authorization in Changzhou city
图16. 常州市专利授权量预测结果
5.5. 需求与供给
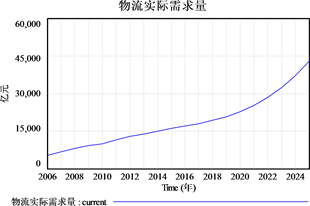
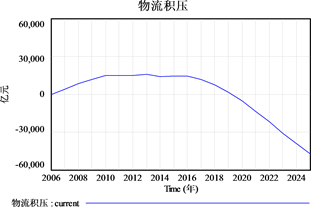
选取“物流实际需求量”、“物流积压”并输出仿真曲线,如图17和图18所示。从图17和图18中分别可以看出,从2006至2016年常州市物流实际需求量稳步提升,在未来的八年里更将快速提升;而物流积压则快速下降。
 资料来源:本文整理绘制。
资料来源:本文整理绘制。
Figure 17. Porecast results of actual logistics demand in Changzhou city
图17. 常州市物流实际需求量预测结果
 资料来源:本文整理绘制。
资料来源:本文整理绘制。
Figure 18. Prediction results of logistics backlog in Changzhou city
图18. 常州市物流积压预测结果
6. 结语
本文在供给侧结构性改革背景下构建了常州市现代物流业竞争力系统动力学模型并进行了模拟仿真分析。常州要实现现代物流业与经济社会环境等的协调发展,政府需加大对教育、科技经费的投入,提升创新动力;促进物流业集约化发展,整合信息资源,从供应链管理角度达到高效、低耗、环保、经济的可持续发展目标;积极调整现代物流业发展方式,提高物流服务质量和效率以满足人们对于高质量生产和生活的需求;积极加大对园林绿地的规划投资建设,为城市营造优美宜人的生活环境,这在一定程度上能够吸引高层次人才,促进城市向可持续发展方式转变。
基金项目
江苏省社会科学基金项目“供给侧改革视野下常州高端制造业创新路径研究”(17XZB007)。