三圈图的极大边修正Szeged指标

doi:10.12677/AAM.2020.910194

期刊菜单

三圈图的极大边修正Szeged指标
Tricyclic Graphs with Maximal Edge Revised Szeged Index

DOI: 10.12677/AAM.2020.910194, PDF, HTML, XML, 国家自然科学基金支持
作者: 王小芳, 刘蒙蒙^*：兰州交通大学数理学院，甘肃兰州
关键词: Wiener指标；修正Szeged指标；边修正Szeged指标；三圈图；Wiener Index； Revised Szeged Index； Edge Revised Szeged Index； Tricyclic Graph

摘要: 边修正Szeged指标

的定义是

，其中m_u(e)和m_v(e)分别是到u的距离比到v的距离近的边的个数和到v的距离比到u的距离近的边的个数，m₀(e)是到u和v距离相等的边数。在本文中，我们得到了连通三圈图的修正边Szeged指标的上界，并且刻画了这些图达到上界的极值。

Abstract: The edge revised Szeged index

is defined as

, where m_u(e) and m_v(e) are, respectively, the number of edges of G lying closer to vertex u than to vertex v and the number of edges of G lying closer to vertex v than to vertex u, and m₀(e) is the number of edges equidistant to u and v. In this paper, we give an upper bound of the edge revised Szeged index for a connected tricyclic graphs, and also characterize those graphs that achieve the upper bound.

文章引用：王小芳, 刘蒙蒙. 三圈图的极大边修正Szeged指标[J]. 应用数学进展, 2020, 9(10): 1672-1685. https://doi.org/10.12677/AAM.2020.910194

1. 引言

本文中所考虑的图都是简单、无向图。文章中的术语和符号请参考 [1]。令 $C_{m}$ 是m条边的圈，G是一个顶点集为 $V (G)$ ，边集为 $E (G)$ 的连通图。对 $u, v \in V (G)$ ， $d (u, v)$ 是u和v之间的距离。G的Wiener指标的定义为

$W (G) = \sum_{{u, v} \subseteq V (G)} d_{G} (u, v)$ .

这一拓扑指标在数学文献中已得到广泛应用，可见 [2] [3]。令 $e = u v$ 是G的一条边，则有如下三个集合：

$N_{u} (e) = {w \in V : d (u, w) < d (v, w)}$ ;

$N_{v} (e) = {w \in V : d (v, w) < d (u, w)}$ ;

$N_{0} (e) = {w \in V : d (u, w) = d (v, w)}$ .

因此， ${N_{u} (e), N_{v} (e), N_{0} (e)}$ 是关于e的一个顶点的划分。 $N_{u} (e)$ ， $N_{v} (e)$ ， $N_{0} (e)$ 的点的个数分别被记为 $n_{u} (e)$ ， $n_{v} (e)$ ， $n_{0} (e)$ 。显然，如果n是图G的顶点数，则有 $n_{u} (e) + n_{v} (e) + n_{0} (e) = n$ 。在文章 [4] 中得到了一个Wiener指标已知性质的公式如下：

$W (T) = \sum_{e = u v \in E (T)} n_{u} (e) n_{v} (e)$ .

这个公式只适用于树T，使用上面的公式Gutman [5] 引入了一个名为Szeged指标的图的不变量作为Wiener指标的拓展并且被定义为

$S z (G) = \sum_{e = u v \in E (G)} n_{u} (e) n_{v} (e)$ .

Randdić [6] 观察到，Szeged指标没有考虑到从一条边的端点到另一条边的距离相等的顶点的贡献，所以他构想出了一个改良版的Szeged指标，叫做修正Szeged指标，连通图G的修正Szeged指标定义为

$S z^{*} (G) = \sum_{e = u v \in E (G)} (n_{u} (e) + \frac{n_{0} (e)}{2}) (n_{v} (e) + \frac{n_{0} (e)}{2})$ .

在 [7] - [12] 中介绍了这些拓扑指数的一些性质和应用。

给定一条边 $e = u v \in E (G)$ ，边e到顶点x之间的距离，用 $d (e, x)$ 表示，定义为

$d (e, x) = \min {d (u, x), d (v, x)}$ .

类似地，集合 $M_{0} (e)$ ， $M_{u} (e)$ 和 $M_{v} (e)$ 被定义为与u和v等距的边的集合，到顶点u的距离小于到顶点v的距离的边的集合，以及到顶点v的距离小于u的边的集合。 $M_{0} (e)$ ， $M_{u} (e)$ 和 $M_{v} (e)$ 的边数分别用 $m_{0} (e)$ ， $m_{u} (e)$ 和 $m_{0} (e)$ 表示。显然，如果m是图G的边数，那么 $m_{u} (e) + m_{v} (e) + m_{0} (e) = m$ 。G的边Szeged指标 [13] 和边修正Szeged指标 [14] 的定义如下：

$S z_{e} (G) = \sum_{e = u v \in E (G)} m_{u} (e) m_{v} (e)$ ,

$S z_{e}^{*} (G) = \sum_{e = u v \in E (G)} (m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2})$ .

边Szeged指标的结果可以在 [15] [16] [17] 中找到。Dong等人在中 [14] 确定了边修正Szeged指标最大和最小的n个顶点的单圈图。在 [18] 中，Liu和Chen给出了一个连通双圈图的边修正Szeged指标的上界，并且描述了那些达到上界的图。在本文中，我们给出了连通三圈图的边修正Szeged指标的一个上界，并对达到上界的图进行了刻画。

定理1.1 设G是一个 $m \geq 37$ 条边的连通三圈图。则有

$S z_{e}^{*} (G) \leq {\begin{cases} \frac{m^{3} - 32}{4}, m 是偶数 \\ \frac{m^{3} - 40}{4}, m 是奇数 \end{cases}$

当且仅当 $G ≅ F_{m}$ 时等号成立(如图1)。

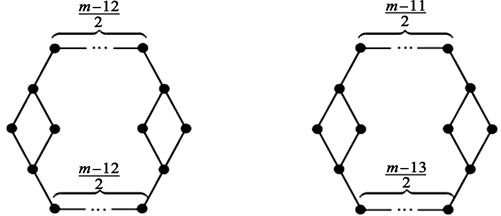m是偶数 m是奇数

Figure 1. The graph for Theorem 1.1

图1. 定理1.1

2. 主要结论

很容易验证

$S z_{e}^{*} (F_{m}) = {\begin{cases} \frac{m^{3} - 32}{4}, m 是偶数 \\ \frac{m^{3} - 40}{4}, m 是奇数 \end{cases}$

即 $F_{m}$ 满足定理1.1的等式。

因此，对于任何大小为m的连通三圈图 $G_{m}$ ，除了 $F_{m}$ 之外， $S z_{e}^{*} (G_{m}) < S z_{e}^{*} (F_{m})$ 。使用 $m_{u} (e) + m_{v} (e) + m_{0} (e) = m$ 这个式子，我们有

$\begin{matrix} S z_{e}^{*} (G) = \sum_{e = u v \in E (G)} (m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2}) \\ = \sum_{e = u v \in E (G)} (\frac{m + m_{u} (e) - m_{v} (e)}{2}) (\frac{m + m_{v} (e) - m_{u} (e)}{2}) \\ = \sum_{e = u v \in E (G)} \frac{m^{2} - {(m_{u} (e) - m_{v} (e))}^{2}}{4} \end{matrix}$

则可以得到

$S z_{e}^{*} (G) = \frac{m^{3}}{4} - \frac{1}{4} \sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2}$ (1)

我们分三种情况来证明定理1.1。首先，我们考虑至少有一条悬挂边的连通三圈图，然后考虑没有悬挂边但是有一个割点的连通三圈图，最后考虑2-连通的三圈图。

2.1. 至少有一条悬挂边的三圈图

引理2.1 设 $G_{m}$ 是一个至少有一条悬挂边的 $m \geq 10$ 条边的三圈图。则

$S z_{e}^{*} (G_{m}) < S z_{e}^{*} (F_{m})$ .

证明设 $e^{'} = x y$ 是图G的一条悬挂边并且 $d (y) = 1$ 。当 $m \geq 10$ 时，有

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq {(m_{x} (e^{'}) - m_{y} (e^{'}))}^{2} = {(m - 1)}^{2} > 40$ .

联立等式(1)，证毕。

2.2. 没有悬挂边但是有一个割点的三圈图

引理2.2 设 $G_{m}$ 是一个没有悬挂边但是有一个割点的 $m \geq 10$ 条边的三圈图。则

$S z_{e}^{*} (G_{m}) < S z_{e}^{*} (F_{m})$ .

证明假设u是一个割点。G是由一个双圈图B和一个圈C组成的且 $V (B) \cup V (C) = {u}$ 。显然 $| E (B) | \geq 5$ 。

如果C是偶圈，对于C中的每条边e，则有 $| m_{u} (e) - m_{v} (e) | = m - | E (C) | = | E (B) |$ 。因此

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq \sum_{e = u v \in E (C)} {(m_{u} (e) - m_{v} (e))}^{2} \geq | E (C) | \cdot {| E (B) |}^{2} \geq 4 \times 5^{2} > 40$ .

如果C是奇圈，对于C中除了xy使得 $d (u, x) = d (u, y)$ 的每条边e，则有 $| m_{u} (e) - m_{v} (e) | = m - | E (C) | = | E (B) |$ 。因此

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq \sum_{e = u v \in E (C)} {(m_{u} (e) - m_{v} (e))}^{2} \geq | E (C) - 1 | \cdot {| E (B) |}^{2} > 2 \times 5^{2} > 40$ .

联立等式(1)，证毕。

2.3. 2-连通的三圈图

在本节中 $κ (G) \geq 2$ ，它必须是(图2)中描述的图形之一。字母 $a, b, \dots, f$ 表示度大于2的顶点之间对应路的长度。为了简单起见，我们将这些路径分别称为 $P (a), P (b), \dots, P (f)$ 。在下面的引语中，我们将图2中的这四个图分别称为 $Θ_{1}$ 、 $Θ_{2}$ 、 $Θ_{3}$ 和 $Θ_{4}$ 。

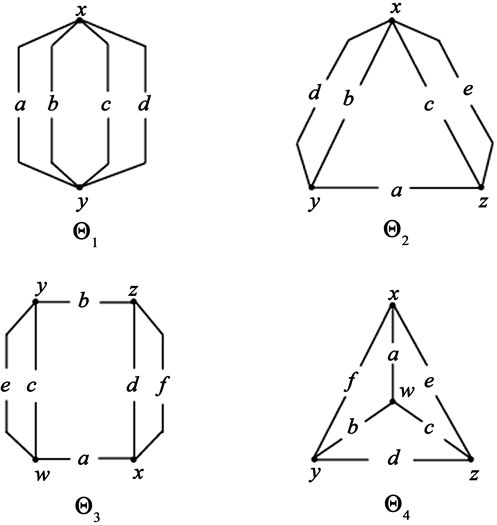
Figure 2. Four cases for 2-connected tricyclic graphs

图2. 2-连通三圈图的四种情况

引理2.3 设 $G_{m}$ 是由路 $P (1), P (2), P (3), P (4)$ 组成的 $Θ_{1}$ 图，且 $e = u v \in E (G)$ 。则有 $| m_{u} (e) - m_{v} (e) | \leq 1$ ，当且仅当e是 $P (1), P (2), P (3), P (4)$ 四条路中奇长路上最中间的那条边。

证明假设 $e = u v \in P (i) (1 \leq i \leq 4)$ ，则关于 $N_{u} (e)$ 和 $N_{v} (e)$ 有以下三种讨论。

情形1 x, y属于不同的集合。我们得到

$| m_{u} (e) - m_{v} (e) | = 2 | b_{i} - a_{i} |$ ,

其中 $a_{i}$ (或 $b_{i}$ )是x(或y)到边e的距离。

假设 $x \in N_{u} (e), y \in N_{v} (e)$ 。则在 $P (i)$ 上 $M_{u} (e)$ 中的边比 $M_{v} (e)$ 上的边多 $a_{i} - b_{i}$ 条，但在 $P (j) (j \neq i)$ 上 $M_{u} (e)$ 中的边比 $M_{v} (e)$ 上的边多 $b_{i} - a_{i}$ 条，因此 $| m_{u} (e) - m_{v} (e) | = | 3 (b_{i} - a_{i}) + (a_{i} - b_{i}) | = 2 | b_{i} - a_{i} |$ 。

情形2 x, y属于相同的集合。我们得到

$| m_{u} (e) - m_{v} (e) | = | E (G) | - g$ ,

其中g是包含边e的最短圈G的长度。

假设 $x, y \in N_{u} (e)$ 。因此所有 $P_{j} (j \neq i)$ 上的边都属于 $M_{u} (e)$ 。由此 $M_{v} (e) = ⌊ \frac{g - 1}{2} ⌋$ ，且 $M_{u} (e) = ⌊ \frac{g - 1}{2} ⌋ + | E (G) | - g$ ，所以 $| m_{u} (e) - m_{v} (e) | = | E (G) | - g$ 。

情形3 x, y其中一个在 $N_{0} (e)$ 中。我们得到

$| m_{u} (e) - m_{v} (e) | \geq 2 a$ ,

当且仅当有三条路 $P_{i} (1 \leq i \leq 4)$ 的长为a时等号成立，其中a是四条路 $P_{i} (1 \leq i \leq 4)$ 中的最短路。

注意到，假设 $x \in N_{u} (e), y \in N_{0} (e)$ 。则包含e的最短圈C是奇圈。设 $z_{j} \in P_{j} (P_{j} ⊄ C)$ 是离e最远的点使得 $z_{j} \in N_{0} (e)$ 。所以

$| m_{u} (e) - m_{v} (e) | = \sum_{j} d (x, z_{j}) \geq \sum_{j} (a + d (y, z_{j})) \geq 2 a$ .

由上可知，在case 2中 $| m_{u} (e) - m_{v} (e) | \geq 4$ ，在case3中 $| m_{u} (e) - m_{v} (e) | \geq 2$ 。因此当且仅当 $x, y$ 在不同的集合中时 $| m_{u} (e) - m_{v} (e) | \leq 1$ ，并且当e在奇长路 $P_{i} (1 \leq i \leq 4)$ 的最中间时， $| b_{i} - a_{i} | = 0$ 。

引理2.4 若 $G_{m}$ 是 $m \geq 12$ 条边的 $Θ_{1}$ 图(见图2)，则有

$S z_{e}^{*} (G_{m}) < S z_{e}^{*} (F_{m})$ .

证明不失一般性，假设 $a \leq b \leq c \leq d$ 。

如果 $a = b = c = d$ ，则 $a \geq 3$ 。先考虑x和y的八条邻边，令 $e = x z$ 是它们其中一条，由引理2.3的情

形1，有 $| m_{x} (e) - m_{z} (e) | \geq 4$ 。所以 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 8 \times 4^{2} > 40$ 。否则，考虑边 $x x_{1} \in P (d)$ ，令C是包含 $x x_{1}$ 的最短圈。若 $y \in N_{x} (x x_{1})$ ，则由引理2.3情形2，有 $| m_{x} (e) - m_{x_{1}} (e) | \geq m - | C |$ 。相同的，对 $y y_{1} \in P (d)$ ，有 $| m_{y} (e) - m_{y_{1}} (e) | \geq m - | C |$ 。

若 $m - | C | \geq 5$ ，有 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 5^{2} > 40$ 。

若 $m - | C | \geq 4$ , $b + c = 4$ , $a \leq 2$ 。因为 $m \geq 12, d \geq 6$ ，所以考虑在 $P (d)$ 上 $x, y$ 到 $e_{i}$ 的距离不超过1的

四条边 $e_{i} (1 \leq i \leq 4)$ ，则有 $| m_{u} (e) - m_{v} (e) | = 4$ ，所以 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 4 \times 4^{2} > 40$ 。

若 $m - | C | \leq 3$ ，不成立。

若 $y \in N_{x_{0}} (x x_{1})$ ，则 $d = a + 1$ 。由 $m \geq 12, a \geq 3$ ，则由引理2.3情形3， $| m_{x} (e) - m_{x_{1}} (e) | = | m_{y} (e) - m_{y_{1}} (e) | \geq 2 a \geq 6$ 。同样的，当 $y y_{1} \in P (d)$ 时， $| m_{y} (e) - m_{y_{1}} (e) | \geq 6$ ，所以

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 6^{2} > 40$ 。

联立等式(1)，证毕。

引理2.5 若 $G_{m}$ 是 $m \geq 12$ 条边的 $Θ_{2}$ 图(见图2)，则有

$S z_{e}^{*} (G_{m}) < S z_{e}^{*} (F_{m})$ .

证明不失一般性，假设 $d \geq b, e \geq c$ 。为了完成接下来的证明，我们考虑下面四种情况。

情形1 $d \geq b + 2$ 。

先考虑 $x x_{1}, y y_{1} \in P (d)$ 这两条边，有

$| m_{x} (e) - m_{x_{1}} (e) | = | m_{y} (e) - m_{y_{1}} (e) | = {\begin{cases} a + c + e, b \leq a + c, \\ b + e, b \geq a + c . \end{cases}$

由此可得

$| m_{x} (e) - m_{x_{1}} (e) | = | m_{y} (e) - m_{y_{1}} (e) | \geq a + c + e$ 。由于 $c + e \geq 3, a + c + e \geq 4$ 。若 $a + c + e \geq 5$ 。则 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 5^{2} > 40$ 。

若 $a + c + e = 4$ ，则 $a = 1, c = 1, e = 2$ 。若 $b \geq 3$ ，有 $b \geq a + c$ ，则有 $| m_{x} (e) - m_{x_{1}} (e) | = | m_{y} (e) - m_{y_{1}} (e) | \geq 5$ ，所以 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 5^{2} > 40$ 。

若 $b = 2$ ，有 $d \geq 6$ .然后考虑一下边 $x x^{'} \in P (e)$ ， $| m_{x} (e) - m_{x^{'}} (e) | \geq 6$ ，则有

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 4^{2} + 6^{2} > 40$ .

情形2 $d = b + 1, e = c + 1$ 。

情形2.1 $a + c - 1 \geq b$ 。

先考虑 $x x_{1} \in P (c)$ ， $x x_{2} \in P (e)$ 。 $| m_{x} (e) - m_{x_{1}} (e) | \geq d - 1 + e - 2$ 。

$| m_{x} (e) - m_{x_{2}} (e) | = {\begin{cases} c + d, c \geq a + b, \\ b + d, c \leq a + d . \end{cases}$

由此可得 $| m_{x} (e) - m_{x_{2}} (e) | \geq d + b = 2 b + 1$ ，所以

${(m_{x} (e) - m_{x_{1}} (e))}^{2} + {(m_{x} (e) - m_{x_{2}} (e))}^{2} > 5 b^{2} + {(e - 2)}^{2} + 2 b e + 1$ .

若 $b \geq 3$ 或 $e \geq 7$ ， $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} > 40$ 。

若 $b \leq 2, e \leq 6$ ，则考虑 $x x^{'} \in P (d)$ 。

若 $b = 1$ ， $| m_{x} (e) - m_{x^{'}} (e) | \geq 6$ ，则 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 10 + 6^{2} > 40$ 。

若 $b = 2$ ， $| m_{x} (e) - m_{x^{'}} (e) | \geq 5$ ，则 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 29 + 5^{2} > 40$ 。

情形2.2 $b \geq a + c + 1$ 。

先考虑 $x x_{1} \in P (b)$ ， $x x_{2} \in P (d)$ 。由 $b \geq a + c + 1$ ，则 $| m_{x} (e) - m_{x_{1}} (e) | = b + e - 1$ ， $| m_{x} (e) - m_{x_{2}} (e) | = b + e$ ，所以 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} = {(b + e - 1)}^{2} + {(b + e)}^{2}$ 。

若 $b \geq 3$ 或 $e \geq 4$ ， $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} > 40$ 。

若 $b \leq 2, e \leq 3$ ，不成立，因为 $b \geq a + c + 1$ 。

情形2.3 $b = a + c$ 。

考虑 $x x_{1} \in P (e)$ ，有 $| m_{x} (e) - m_{x_{1}} (e) | = d - 1 + b = 2 b$ 。

若 $b \geq 4$ ，则有 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq {(m_{x} (e) - m_{x_{1}} (e))}^{2} \geq 8^{2} > 40$ 。

若 $b = 3$ ，则考虑边 $x x^{'} \in P (d)$ ，可以得到 $| m_{x} (e) - m_{x^{'}} (e) | = a + c + e \geq 5$ ，则有 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 6^{2} + 5^{2} > 40$ 。

若 $b = 2$ ，则有 $a - c - 1, e = 2, d = 3$ ，由于 $m \geq 12$ ，所以不成立。

情形3 $d = b + 1, e = c \geq 2$ 。

情形3.1 $a + c - 1 \geq b$ 。

先考虑 $x x_{1} \in P (c)$ 和 $x x_{2} \in P (e)$ ，有

$| m_{x} (e) - m_{x_{1}} (e) | = | m_{x} (e) - m_{x_{2}} (e) | \geq d - 1 + c - 1$ .

由于 $d \geq 2, c \geq 2, d + c \geq 4$ ，若 $d + c \geq 7$ ，有

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 5^{2} > 40$ .

当 $4 \leq d + c \leq 6$ 时，考虑边 $x x^{'} \in P (d)$ 。

若 $d = 3, c = 3$ ，则 $b = 2, e = 3, a \geq 1$ ， $| m_{x} (e) - m_{x^{'}} (e) | \geq 6$ ，所以

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 4^{2} + 6^{2} > 40$ .

若 $d = 4, c = 2$ ，则 $b = 3, e = 2, a \geq 2$ ， $| m_{x} (e) - m_{x^{'}} (e) | \geq 5$ ，所以

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 4^{2} + 5^{2} > 40$ .

若 $d = 2, c = 4$ ，则 $b = 1, e = 4, a \geq 1$ ， $| m_{x} (e) - m_{x^{'}} (e) | \geq 6$ ，所以

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 4^{2} + 6^{2} > 40$ .

若 $d = 3, c = 2$ ，则 $b = e = 2, a \geq 3$ ， $| m_{x} (e) - m_{x^{'}} (e) | \geq 5$ ，所以

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 3^{2} + 5^{2} > 40$ .

若 $d = 2, c = 3$ ，则 $b = 1, e = 3, a \geq 3$ ， $| m_{x} (e) - m_{x^{'}} (e) | \geq 6$ ，所以

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 3^{2} + 6^{2} > 40$ .

若 $d = 2, c = 2$ ，则 $b = 1, e = 2, a \geq 5$ ， $| m_{x} (e) - m_{x^{'}} (e) | \geq 6$ ，所以

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 2^{2} + 6^{2} > 40$ .

情形3.2 $b \geq a + c - 1$ 。

考虑 $x x_{1} \in P (c)$ ，由 $b \geq a + c - 1$ ，有 $y \in N_{x_{1}} (x x_{1})$ 。令u是 $P (d)$ 上最远的点使得 $u \in N_{x} (x x_{1})$ ， $u^{'}$ 是u的邻点但是它不在集合 $N_{x} (x x_{1})$ 中，如果圈 $P (d) \cup P (c) \cup P (a)$ 是偶圈，则有 $d (u, x) = d (u^{'}, y) + a + c - 1$ ，即 $d (u, x) - d (u^{'}, y) = a + c - 1$ 。如果圈 $P (d) \cup P (c) \cup P (a)$ 是奇圈，则有 $d (u, x) + 1 = d (u^{'}, y) + a + c - 1$ ，即 $d (u, x) + 1 - d (u^{'}, y) = a + c - 1$ 。所以 $| m_{x} (e) - m_{x_{1}} (e) | = e - 1 + a + c - 1 = a + 2 c - 2$ 。相同的，对于边 $x x_{2} \in P (e)$ 有 $| m_{x} (e) - m_{x_{2}} (e) | = a + 2 c - 2$ 。

由于 $c \geq 2, a + 2 c \geq 5$ 。如果 $a + 2 c \geq 7$ ，则

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 5^{2} > 40$ .

若 $a + 2 c = 6$ ，即 $a = c = e = 2$ ，有 $b \geq 3$ 。然后考虑 $x x^{'} \in P (d)$ ， $| m_{x} (e) - m_{x^{'}} (e) | = b + e \geq 5$ ，所以

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 4^{2} + 5^{2} > 40$ .

若 $a + 2 c = 5$ ，即 $a = 1, c = e = 2$ ，有 $b \geq 3$ 。然后考虑 $x x^{'} \in P (d)$ ， $| m_{x} (e) - m_{x^{'}} (e) | = b + e \geq 5$ ，所以

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 3^{2} + 5^{2} > 40$ .

情形4 $d = b, e = c$ 。

情形4.1 $d = b = e = c \geq 2$ 。

考虑边 $x x_{1} \in P (e)$ ，有 $| m_{x} (e) - m_{x_{1}} (e) | = c - 1 + d = 2 e - 1$ 。对于x的其他三条邻边也是一样的。

如果 $e \geq 3$ ，则 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 4 \times 5^{2} > 40$ 。

如果 $e = 2$ ，然后考虑 $P (a)$ 上的边 $y y^{'}, z z^{'}$ ， $| m_{y} (e) - m_{y^{'}} (e) | = | m_{z} (e) - m_{z^{'}} (e) | \geq d + 1 \geq 3$ 。

所以 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 6 \times 3^{2} > 40$ 。

情形4.2 $d = b > e = c \geq 2$ 。

考虑边 $x x_{1} \in P (b)$ ， $| m_{x} (e) - m_{x_{1}} (e) | = d - 1 + e$ 。同样对于 $x x_{2} \in P (d)$ ， $| m_{x} (e) - m_{x_{2}} (e) | = d - 1 + e$ 。

若 $d + e \geq 6$ ，则有 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 5^{2} > 40$ 。

若 $d + e = 5$ ，即 $d = 3, e = 2$ 。然后考虑 $x x^{'} \in P (c)$ ， $| m_{x} (e) - m_{x^{'}} (e) | \geq e - 1 + d = 4$ 。则有

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 4^{2} + 4^{2} > 40$ 。

联立等式(1)，证毕。

引理2.6 若 $G_{m}$ 是 $m \geq 12$ 条边的 $Θ_{3}$ 图(见图2)，则有，

$S z_{e}^{*} (G_{m}) < S z_{e}^{*} (F_{m})$ .

证明不失一般性，假设 $f \geq d, e \geq c$ ，为了完成证明，我们考虑以下四种情况。

情形1 $e \geq c + 2$ 。

考虑边 $w w_{1}, y y_{1} \in P (e)$ ，

$| m_{w} (e) - m_{w_{1}} (e) | = | m_{y} (e) - m_{y_{1}} (e) | = {\begin{cases} a + b + d + f, c \leq a + b + d, \\ c + f, c \geq a + b + d . \end{cases}$

由此可得 $| m_{w} (e) - m_{w_{1}} (e) | = | m_{y} (e) - m_{y_{1}} (e) | \geq a + b + d + f$ 。因为 $d + f \geq 3$ ，所以 $a + b + d + f \geq 5$ ，则有 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 5^{2} > 40$ 。

情形2 $e = c + 1, f = d + 1$ 。

情形2.1 $a + c - 1 \geq b + d$ 。

先考虑 $y y_{1} \in P (c)$ ， $y y_{2} \in P (e)$ 。 $| m_{y} (e) - m_{y_{1}} (e) | \geq e - 2 + f - 1 = c + d - 1$ 。

$| m_{y} (e) - m_{y_{2}} (e) | = {\begin{cases} b + d + f, c \leq a + b + d, \\ c + f, c \geq a + b + d . \end{cases}$

由此可得 $| m_{y} (e) - m_{y_{2}} (e) | \geq d + b + f = b + 2 d + 1$ ，所以

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq {(c + d - 1)}^{2} + {(b + 2 d + 1)}^{2}$ .

若 $b \geq 4$ 或 $c \geq 5$ 或 $d \geq 3$ ，则 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} > 40$ 。

若 $b \leq 3, c \leq 4, d \leq 2$ ，则考虑 $w w^{'} \in P (e), z z^{'} \in P (f)$ 。

若 $d = 2$ ，有 $| m_{w} (e) - m_{w^{'}} (e) | \geq 4$ ， $| m_{z} (e) - m_{z^{'}} (e) | \geq 4$ 则

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 3^{2} + 2 + 3^{2} + 5^{2} > 40$ .

若 $d = 1$ ，有 $| m_{w} (e) - m_{w^{'}} (e) | \geq 3$ ， $| m_{z} (e) - m_{z^{'}} (e) | \geq 5$ 则

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 2^{2} + 2 + 3^{2} + 5^{2} > 40$ .

情形2.2 $a + c \leq b + d - 1$ 。

这部分的证明和Subcase 2.1的过程类似的。

情形2.3 $a + c = b + d$ 。

先考虑 $y y_{1} \in P (e)$ ， $x x_{1} \in P (f)$ 。 $| m_{y} (e) - m_{y_{1}} (e) | \geq b + d + f - 1$ 。 $| m_{x} (e) - m_{x_{1}} (e) | = a + c + e - 1$ 。 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq {(a + c + d)}^{2} + {(a + 2 c)}^{2}$ 。

若 $a \geq 3$ 或 $c \geq 2$ 或 $d \geq 3$ ， $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} > 40$ 。

若 $a \leq 2, c \leq 1, d \leq 3$ ，不成立，因为 $m \geq 12$ 。

情形3 $a + d - 1 \geq b + c$ 。

情形3.1 $a + d - 1 \geq b + c$ 。

先考虑 $z z_{1} \in P (d)$ ， $| m_{z} (e) - m_{z_{1}} (e) | \geq e - 1 + f - 1 = c + d - 1$ 。同样的，对于 $z z_{2} \in P (f)$ ，有 $| m_{z} (e) - m_{z_{2}} (e) | = c + d - 1$ 。

因为 $d \geq 2$ ，否则G就不说简单图，所以 $c + d \geq 3$ 。

若 $c + d \geq 6$ ，则 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 5^{2} > 40$ 。

若 $c + d = 5$ ，有 $| m_{z} (e) - m_{z_{1}} (e) | = | m_{z} (e) - m_{z_{2}} (e) | \geq 4$ ，然后考虑边 $w w^{'} \in P (e)$ 。

若 $c = 1, d = 4$ ，有 $| m_{w} (e) - m_{w^{'}} (e) | \geq 5$ ，则

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 4^{2} + 5^{2} > 40$ .

若 $c = 2, d = 3$ ，有 $| m_{w} (e) - m_{w^{'}} (e) | \geq 5$ ，则

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 4^{2} + 5^{2} > 40$ .

若 $c = 3, d = 2$ ，有 $| m_{w} (e) - m_{w^{'}} (e) | \geq 5$ ，则

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 4^{2} + 5^{2} > 40$ .

若 $c + d = 4$ ，有 $| m_{z} (e) - m_{z_{1}} (e) | = | m_{z} (e) - m_{z_{2}} (e) | \geq 3$ ，则考虑边 $w w^{'}, y y^{'} \in P (e)$ .

若 $c = 1, d = 3$ ，有 $| m_{w} (e) - m_{w^{'}} (e) | \geq 4$ ， $| m_{y} (e) - m_{y^{'}} (e) | \geq 4$ 则

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 3^{2} + 2 \times 4^{2} > 40$ .

若 $c = 2, d = 2$ ，有 $| m_{w} (e) - m_{w^{'}} (e) | \geq 4$ ， $| m_{y} (e) - m_{y^{'}} (e) | \geq 5$ 则

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 3^{2} + 4^{2} + 5^{2} > 40$ .

若 $c + d = 3$ ，即 $c = 1, d = 2$ 有 $| m_{z} (e) - m_{z_{1}} (e) | = | m_{z} (e) - m_{z_{2}} (e) | \geq 2$ ，则考虑边 $w w^{'}, y y^{'} \in P (e)$ 。有 $| m_{w} (e) - m_{w^{'}} (e) | \geq 5$ ， $| m_{y} (e) - m_{y^{'}} (e) | \geq 5$ ，于是

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 2^{2} + 2 \times 5^{2} > 40$ .

情形3.2 $a + d \leq b + c$ 。

先考虑边 $w w_{1} \in P (e)$ ，有

$| m_{w} (e) - m_{w_{1}} (e) | = {\begin{cases} a + d + f, c \leq a + b + d, \\ c + f, c \geq a + b + d . \end{cases}$

于是， $| m_{w} (e) - m_{w_{1}} (e) | \geq a + d + f = a + 2 d \geq 5$ 。

若 $a + 2 d \geq 7$ ，则 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 7^{2} > 40$ 。

若 $a + 2 d = 6$ ，即 $a = 2, d = 2$ 。然后考虑边 $y y^{'} \in P (e)$ 。有 $| m_{y} (e) - m_{y^{'}} (e) | \geq 4$ ，则 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 6^{2} + 4^{2} > 40$ 。

若 $a + 2 d = 5$ ，即 $a = 1, d = 2$ 。然后考虑边 $y y^{'} \in P (e)$ 。有 $| m_{y} (e) - m_{y^{'}} (e) | \geq 4$ ，则 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 5^{2} + 4^{2} > 40$ 。

情形4 $d = f, e = c$ 。

先设 $a \leq b$ 。

情形4.1 $c = e > d = f \geq 2$ 。

先考虑 $w w_{1} \in P (e)$ ， $| m_{w} (e) - m_{w_{1}} (e) | \geq f + c - 1$ 。同样的，对于 $w w_{2} \in P ( c )$

有 $| m_{w} (e) - m_{w_{2}} (e) | = f + c - 1$ 。

由 $c \geq 3$ 且 $f \geq 2$ ，有 $c + f \geq 5$ 。若 $c + f \geq 6$ ，有 $| m_{w} (e) - m_{w_{1}} (e) | = | m_{w} (e) - m_{w_{2}} (e) | \geq 5$ ，则 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 5^{2} > 40$ .

若 $c + f = 5$ ，即 $c = 3, f = 2$ 。有 $| m_{w} (e) - m_{w_{1}} (e) | = | m_{w} (e) - m_{w_{2}} (e) | = 4$ 。

若 $b > a$ ，则考虑边 $x x_{1} \in P (d), x x_{2} \in P (f)$ ， $| m_{x} (e) - m_{x_{1}} (e) | = | m_{x} (e) - m_{x_{2}} (e) | \geq 3$ 。则 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 4^{2} + 2 \times 3^{2} > 40$ .

若 $b = a$ ，则考虑路 $P (d)$ 和 $P (f)$ 上的四条边， $| m_{x} (e) - m_{x_{i}} (e) | = | m_{z} (e) - m_{x_{i}} (e) | = 2 (1 \leq i \leq 2)$ 。则 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 4^{2} + 4 \times 2^{2} > 40$ .

情形4.2 $c = e = d = f \geq 3$ 。

先考虑 $w w_{1} \in P (e)$ ， $w w_{2} \in P (c)$ ， $x x_{1} \in P (d)$ ， $x x_{2} \in P (f)$ 这四条边。 $| m_{w} (e) - m_{w_{i}} (e) | = | m_{x} (e) - m_{x_{i}} (e) | \geq f - 1 + c - 1 = 2 (c - 1) \geq 4 (1 \leq i \leq 2)$ ，则 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 4 \times 4^{2} > 40$ .

情形4.3 $c = e = d = f = 2$ 。

若 $b \geq a + 3$ ，考虑 $w w_{1} \in P (e)$ ， $w w_{2} \in P (c)$ ， $x x_{1} \in P (d)$ ， $x x_{2} \in P (f)$ 这四条边。 $| m_{w} (e) - m_{w_{i}} (e) | = | m_{x} (e) - m_{x_{i}} (e) | \geq f + c - 1 = 3 (1 \leq i \leq 2)$ 。然后考虑 $P (b)$ 上的两条边 $y y_{1}, z z_{1}$ ，有 $| m_{w} (e) - m_{w_{i}} (e) | = | m_{x} (e) - m_{x_{i}} (e) | \geq f + c - 1 = 3 (1 \leq i \leq 2)$ 。则 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 4 \times 3^{2} + 2 \times 2^{2} > 40$ 。

若 $b = a + 2$ ，则m是偶数，我们只需证明 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} > 32$ 。先考虑 $w w_{1} \in P (e)$ ， $w w_{2} \in P (c)$ ， $x x_{1} \in P (d)$ ， $x x_{2} \in P (f)$ 这四条边。 $| m_{w} (e) - m_{w_{i}} (e) | = | m_{x} (e) - m_{x_{i}} (e) | \geq f + c - 1 = 3 (1 \leq i \leq 2)$ 。则 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} > 32$ 。

若 $b = a + 1$ ，则我们得到的图是m是奇数时的 $F_{m}$ 。如果 $b = a$ ，则我们得到的图是m是偶数时的 $F_{m}$

联立等式(1)，证毕。

引理2.7 若 $G_{m}$ 是 $m \geq 37$ 条边的 $Θ_{4}$ 图(见图2)，则有，

$S z_{e}^{*} (G_{m}) < S z_{e}^{*} (F_{m})$ .

证明不失一般性，假设 $a = \max {a, b, c, d, e, f}$ 。因为 $m \geq 37$ ，所以 $a \geq 7$ .考虑边 $w w_{1} \in P (a)$ 。由a的选择可知 $d (z, w) \leq d (z, w_{1})$ ，所以 $z \in N_{w} (w w_{1})$ 或 $z \in N_{0} (w w_{1})$ 。当且仅当 $a = c \leq b + d$ 且 $e = 1$ 时

$z \in N_{0} (w w_{1})$ 。对于y我们可以得到同样的结果.。下面，令C是包含 $w w_{1}$ 的最短圈。当 $a > \frac{| C | + 1}{2}$ 时， $x \in N_{w} (w w_{1})$ ；当 $a = \frac{| C | + 1}{2}$ 时， $x \in N_{0} (w w_{1})$ ；当 $a < \frac{| C | + 1}{2}$ 时， $x \in N_{w_{1}} (w w_{1})$ 。

情形1 $a > \frac{| C | + 1}{2}$ 。

因为 $x \in N_{w} (w w_{1})$ ，可以得到 $y, z \in N_{w} (w w_{1})$ 。则有 $| m_{w} (e) - m_{w_{1}} (e) | = m - | C |$ 。同样的，对于 $x x_{1} \in P (a)$ ，有 $| m_{x} (e) - m_{x_{1}} (e) | = m - | C |$ 。

若 $m - | C | \geq 5$ ，有 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 2 \times 5^{2} > 40$ 。

若 $m - | C | = 4$ ，且C是由 $P (a)$ ， $P (f)$ 和 $P (b)$ 组成， $e + c + d = 4, f + b \leq 3$ 。由 $m \geq 37$ ，有 $a \geq 30$ 。下面考虑 $P (a)$ 上的四条边 $e_{i} (1 \leq i \leq 4)$ 使得 $e_{i}$ 到x或w的距离不超过1，则有 $| m_{u} (e_{i}) - m_{v} (e_{i}) | = 4$ ，所以

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 4 \times 4^{2} > 40$ .

若 $m - | C | = 4$ ，且C是由 $P (a)$ ， $P (f)$ ， $P (d)$ 和 $P (c)$ 组成，若 $b \geq 3$ ，则 $P (a) \cup P (c) \cup P (e)$ 是包含边 $w w_{1}$ 的最短圈，矛盾。因此 $b = 2$ ，这种情况和C由 $P (a)$ ， $P (f)$ ， $P (b)$ 组成的证明是一样的。

若 $m - | C | = 3$ ，且C是由 $P (a)$ ， $P (f)$ ，和 $P (b)$ 组成， $e + c + d = 3, f + b = 2$ 。由 $m \geq 37$ ，有 $a \geq 32$ 。下面考虑 $P (a)$ 上的六条边 $e_{i} (1 \leq i \leq 6)$ 使得 $e_{i}$ 到x或w的距离不超过2，则有 $| m_{u} (e_{i}) - m_{v} (e_{i}) | = 3$ ，所以

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 6 \times 3^{2} > 40$ .

若 $m - | C | = 3$ ，且C是由 $P (a)$ ， $P (f)$ ， $P (d)$ 和 $P (c)$ 组成，若 $b = 2, e = 1$ ，则 $P (a) \cup P (c) \cup P (e)$ 是包含边 $w w_{1}$ 的最短圈，若 $b = 1, e = 2$ ，则圈 $P (a) \cup P (b) \cup P (f)$ 比圈 $P (a) \cup P (f) \cup P (d) \cup P (c)$ 的长度更短，矛盾。

若 $m - | C | = 2$ ，不成立。

情形2 $a = \frac{| C | + 1}{2}$ 。

情形2.1 C由 $P (a)$ ， $P (f)$ ， $P (d)$ 和 $P (c)$ 组成。

在这种情况下 $y, z \in N_{w} (w w_{1})$ 且 $b \geq d + c$ 。令u是 $P (e)$ 上最远的点使得 $u \in N_{w} (w w_{1})$ ， $u^{'}$ 是u的邻点但是它不在集合 $N_{w} (w w_{1})$ 中，如果圈 $P (a) \cup P (c) \cup P (e)$ 是偶圈，则有 $d (u, z) + c = d (u^{'}, x) + a - 1$ ，即 $d (u, z) = d (u^{'}, x) + a - c - 1$ 。如果圈 $P (a) \cup P (c) \cup P (e)$ 是奇圈，则有 $d (u, z) + 1 + c = d (u^{'}, x) + a - 1$ ，即 $d (u, z) + 1 = d (u^{'}, x) + a - c - 1$ 。所以 $| m_{w} (e) - m_{w_{1}} (e) | = d (u, z) + b \geq d (u^{'}, x) + a - c - 1 + b \geq a \geq 7$ 。所以

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 7^{2} > 40$ .

情形2.2 C由 $P (a)$ ， $P (f)$ 和 $P (b)$ 组成。

在这种情况下 $y \in N_{w} (w w_{1})$ 且 $b \leq d + c$ 。

若 $z \in N_{0} (w w_{1})$ ，则有 $a = c \leq b + d$ 且 $e = 1$ 。因为 $x z \in M_{0} (w w_{1})$ ，所以 $| m_{w} (e) - m_{w_{1}} (e) | \geq c \geq 7$ ，因此

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 7^{2} > 40$ .

若 $z \in N_{w} (w w_{1})$ ，与Subcase 2.1相类似的，令u是 $P (e)$ 上最远的点使得 $u \in N_{w} (w w_{1})$ ， $u^{'}$ 是u的邻点但是它不在集合 $N_{w} (w w_{1})$ 中，则有

$d (u, z) \geq {\begin{cases} a - c - 1, c \leq b + d, \\ a - (b + d) - 1, c \geq b + d . \end{cases}$

于是有 $| m_{w} (e) - m_{w_{1}} (e) | \geq d + c + a - 1 \geq a \geq 7$ ，因此

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 7^{2} > 40$ .

情形3 $a < \frac{| C | + 1}{2}$ 。

情形3.1 $y, z \in N_{0} (w w_{1})$ 。

在这种情况下， $a = b = c, e = f = 1$ ，则 $| m_{w} (e) - m_{w_{1}} (e) | = c - e \geq a - 1 \geq 6$ 。然后考虑边 $x x^{'} \in P (a)$ ，则 $y \in N_{x} (x x^{'}), z \in N_{x} (x x^{'}), w \in N_{x^{'}} (x x^{'})$ ，在圈C上只有一条边在集合 $M_{x^{'}} (x x^{'})$ 中，其它边都在集合 $M_{x} (x x^{'})$ 中，所以 $| m_{x} (e) - m_{x^{'}} (e) | = c - 1 - 1 + e \geq 6$ ，因此

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 6^{2} + 6^{2} > 40$ .

情形3.2 $y, z$ 其中有一个在集合 $N_{w} (w w_{1})$ 中。

在这种情况下，我们可以得到

$| m_{w} (e) - m_{w_{1}} (e) | \geq {\begin{cases} a + d - 1, b \leq c + d, \\ a - c - 1 + b, b \geq c + d . \end{cases}$

则有 $| m_{w} (e) - m_{w_{1}} (e) | \geq a + d - 1 \geq a \geq 7$ 。因此

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 7^{2} > 40$ .

情形3.3 $y, z$ 其中有一个在集合 $N_{0} (w w_{1})$ 中。

首先假设 $z \in N_{0} (w w_{1})$ ，则 $a = c \leq b + d, e = 1$ 。

若 $z \notin V (C)$ ， $C = P (a) \cup P (f) \cup P (b)$ 。则有 $| m_{w} (e) - m_{w_{1}} (e) | \geq a - 1 \geq 6$ ， $| m_{x} (e) - m_{x_{1}} (e) | \geq a - 1 \geq 6$ ，因此

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 6^{2} + 6^{2} > 40$ .

若 $z \in V (C)$ ， $C = P (a) \cup P (e) \cup P (c)$ 。否则 $C = P (a) \cup P (f) \cup P (d) \cup P (c)$ ，因为 $z \in N_{0} (w w_{1})$ ，所以 $y \in N_{w_{1}} (w w_{1})$ ，矛盾。令u是 $P (f)$ 上最远的点使得 $u \in N_{w} (w w_{1})$ ， $u^{'}$ 是u的邻点但是它不在集合 $N_{w} (w w_{1})$ 中，如果圈 $P (a) \cup P (f) \cup P (b)$ 是偶圈，则有 $d (u, y) + b = d (u^{'}, x) + a - 1$ ，即 $d (u, y) - d (u^{'}, x) + a - b - 1$ 。如果圈 $P (a) \cup P (f) \cup P (b)$ 是奇圈，则有 $d (u, y) + 1 + b = d (u^{'}, x) + a - 1$ ，即 $d (u, y) + 1 - d (u^{'}, x) = a - b - 1$ 。

$| m_{w} (e) - m_{w_{1}} (e) | \geq b + a - b - 1 \geq a - 1 \geq 6$ 。然后考虑 $P (a)$ 上的边 $x x^{'}$ 。在这种情况下我们可以得到 $w \in N_{x^{'}} (x x^{'}), z \in N_{x} (x x^{'})$ 。如果 $y \in N_{x} (x x^{'})$ ，则有 $| m_{x} (e) - m_{x^{'}} (e) | \geq a - f - 1 + f + d \geq a \geq 7$ 。所以 $\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 6^{2} + 7^{2} > 40$ 。如果 $y \in N_{0} (x x^{'})$ ，即 $f = a, b = 1$ 。则有 $| m_{x} (e) - m_{x^{'}} (e) | \geq a - 1 \geq 6$ ，所以

$\sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} \geq 6^{2} + 6^{2} > 40$ .

联立等式(1)，证毕。

从引理2.1，2.2，2.4，2.5，2.6，2.7，我们证明了定理1.1。

注：事实上，当 $m \geq 25$ 时，定理1.1也可以被证明，不过这需要更多的一些细节。

基金项目

国家自然科学基金(No. 11961040)；甘肃省教育厅基金(No. 2019A-037)。

NOTES

^*通讯作者。

参考文献

[1]	Bondy, J.A. and Murty, U.S.R. (2008) Graph Theory, GTM 244. Springer, Berlin. https://doi.org/10.1007/978-1-84628-970-5
[2]	Gutman, I., Klavzar, S. and Mohar, B. (1997) Fifty Years of the Wiener Index. MATCH Communications in Mathematical and in Computer Chemistry, 35, 1-259.
[3]	Gutman, I., Yeh, Y.N., Lee, S.L. and Luo, Y.L. (1993) Some Recent Results in the Theory of the Wiener Number. Indian Journal of Chemistry, 32A, 651-661.
[4]	Wiener, H. (1947) Structural Determination of Paraffin Boiling Points. Journal of the American Chemical Society, 69, 17-20. https://doi.org/10.1021/ja01193a005
[5]	Gutman, I. (1994) A Formula for the Wiener Number of Trees and Its Extension to Graphs Containing Cycles. Graph Theory Notes of New York, 27, 9-15.
[6]	Randic, M. (2002) On Generalization of Wiener Index for Cyclic Structures. Acta Chimica Slovenica, 49, 483-496. https://doi.org/10.1201/b14725-23
[7]	Chen, L., Li, X. and Liu, M. (2014) Tricyclic Graphs with Maximal Revised Szeged Index. Discrete Applied Mathematics, 177, 71-79. https://doi.org/10.1016/j.dam.2014.05.034
[8]	Li, X. and Liu, M. (2013) Bicyclic Graphs with Maximal Revised Szeged Index. Discrete Applied Mathematics, 161, 2527-2531. https://doi.org/10.1016/j.dam.2013.04.002
[9]	Pisanski, T. and Randic, M. (2010) Use of the Szeged Index and the Revised Szeged Index for Measuring Network Bipartivity. Discrete Applied Mathematics, 158, 1936-1944. https://doi.org/10.1016/j.dam.2010.08.004
[10]	Pisanski, T. and Zerovnik, J. (2009) Edge-Contributions of Some Topological Indices and Arboreality of Molecular Graphs. Ars Mathematica Contemporanea, 2, 49-58. https://doi.org/10.26493/1855-3974.68.51b
[11]	Simic, S., Gutman, I. and Baltic, V. (2000) Some Graphs with Extremal Szeged Index. Mathematica Slovaca, 50, 1-15.
[12]	Xing, R. and Zhou, B. (2011) On the Revised Szeged Index. Discrete Applied Mathematics, 159, 69-78. https://doi.org/10.1016/j.dam.2010.09.010
[13]	Gutman, I. and Ashrafifi, A.R. (2008) The Edge Version of the Szeged Index. Croatica Chemica Acta, 81, 263-266.
[14]	Dong, H., Zhou, B. and Trinajstic, C. (2011) A Novel Version of the Edge-Szeged Index. Croatica Chemica Acta, 84, 543-545. https://doi.org/10.5562/cca1889
[15]	Cai, X. and Zhou, B. (2010) Edge Szeged Index of Unicyclic Graphs. MATCH Communications in Mathematical and in Computer Chemistry, 63, 133-144.
[16]	Khalifeh, M.H., Yousefifi-Azari, H., Ashrafifi, A.R. and Gutman, I. (2008) The Edge Szeged Index of Product Graphs. Croatica Chemica Acta, 81, 277-281.
[17]	Vukicevic, D. (2009) Note on the Graphs with the Greatest Edge-Szeged Index. MATCH Communications in Mathematical and in Computer Chemistry, 61, 673-681.
[18]	Liu, M. and Chen, L. (2016) Bicyclic Graphs with Maximal Edge Revised Szeged Index. Discrete Applied Mathematics, 215, 225-230. https://doi.org/10.1016/j.dam.2016.07.005

为你推荐

友情链接