预瞄主动悬架自抗扰控制

Preview Control Active Suspension Based on Active Disturbance Rejection Control

摘要: 预瞄主动悬架系统可获得车辆前方的路面不平度，这使悬架控制系统能够提前应对即将到来的路面激励。为了使预瞄主动悬架控制系统能够适应不同的车速，同时考虑轮胎对路面的滤波效应，本文提出了一种预瞄主动悬架的控制方法。该方法使用轮胎弹性滚子接触模型计算路面不平度的有效路形。基于主动退让路面冲击或支撑车身的控制策略，将预瞄路面的有效路形作为控制器的控制参考信号。以1/4车辆模型为被控对象设计自抗扰控制器，使悬架动行程根据预知的有效路形变化，从而实现预瞄控制。分别在5~60 km/h和5~100 km/h的车速条件下进行了脉冲输入路面仿真和随机路面仿真。结果表明，预瞄控制系统能明显减小车身垂向振动，在脉冲输入下的最高有效车速是30 km/h，在随机输入下的最高有效车速是50 km/h。因此该预瞄控制方法能够适应不同的车速。

Abstract: The preview system on active suspensions can obtain road irregularities in front of the vehicle, so that the suspension control system can prepare for the oncoming road excitation. In order to improve the adaptability of the preview system on active suspensions to different speeds, also taking into account the filter effect of tires to pavements, a preview control method of active suspension is proposed in this paper. The preview control method uses the tire flexible roller contact model to calculate the effective road input of road irregularities. The control strategy is receding the road impact or supporting the vehicle body actively. Based on the strategy, the effective road input is the control reference signal of the controller. An active disturbance rejection controller is designed to control a quarter vehicle model, making the suspension deflection follow the effective road input of the preview road. Simulation experiments were carried out under impulse input and random input at speed range of 5~60 km/h and 5~100 km/h respectively. The simulation results demonstrate that the preview control system can reduce the vehicle body vibration effectively. The maximum effective speed of impulse input and random input is 30 km/h and 50 km/h respectively. The preview control method can adapt to different speeds.

1. 前言

主动悬架可以提升车辆的行驶平顺性和操纵稳定性。预瞄主动悬架控制系统提前获得车辆前方道路的不平度信息并将其用于悬架控制，可进一步改善主动悬架的控制效果，同时减少控制系统的能耗 [1]。近年来，关于预瞄主动悬架的研究主要集中于路面不平度信息的获取和实时处理问题 [2] [3] [4]，以及实车应用的验证 [5] [6] [7]。控制系统处理道路不平度信息的速度和准确性有待提高，并且在实时控制时需要解决计算量过大的问题。在现有的研究中，通常将预瞄控制问题作为输入时滞问题。处理输入时滞的方法有Padé近似法 [8] [9] 和离散状态空间法等 [10]。在控制器中取定的时滞时间就是预瞄时间，导致控制器不能适应车速的变化。而且在上述研究中，通常直接将预瞄路面的不平度作为悬架将要受到的垂向激励。但实际轮胎对路面不平度输入具有滤波作用，由传感器测量得到的路面不平度并非悬架将要受到的垂向激励。因此轮胎滤波效应对预瞄控制的影响值得研究。

为了使预瞄控制系统能适应车速变化，并考虑轮胎包容特性对路面的滤波作用，本文提出一种预瞄主动悬架的控制方法。该方法使用轮胎弹性滚子接触模型计算路面不平度的有效路形，可以仿真任意短波长不平路面对车辆的输入，同时作为悬架动行程的控制参考信号。考虑实际车辆存在无法建模的非线性和不确定性，基于自抗扰控制(Active Disturbance Rejection Control, ADRC)设计了控制器，使悬架动行程跟随预瞄路面的有效路形变化，从而实现预瞄控制。为了验证预瞄控制系统的有效性，在脉冲输入路面和随机路面进行了仿真试验。

2. 1/4车辆模型及预瞄控制方法

2.1. 1/4车辆模型

以1/4车辆模型为研究对象，如图1所示。其中m_b表示簧载质量，m_w表示非簧载质量，K_s是悬架弹簧的刚度，C_s是减振器的阻尼，U是主动悬架执行器的控制力。忽略轮胎的阻尼，以K_t表示轮胎的垂向刚度。以z_b表示簧载质量的质心垂向位移，以z_w表示非簧载质量的质心垂向位移，z_r表示轮胎接地点处的路面输入，且规定z_b、z_w和z_r以向上为正方向。悬架动行程z_w-z_b以压缩为正，控制力U以使悬架压缩的方向为正，即U为正时，m_b受到向下的控制力，而m_w受到向上的控制力。车辆模型的参数如表1所示。

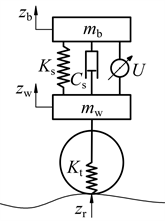
Figure 1. Quarter-car active suspension model

图1. 1/4车辆模型

当双质量振动系统在平衡位置附近振动时，1/4车辆的运动学方程为

$\{\begin{array}{l}{m}_{\text{b}}{\ddot{z}}_{\text{b}}=K_{\text{s}}\left(z_{\text{w}}-z_{\text{b}}\right)+C_{\text{s}}\left({\stackrel{\dot{}}{z}}_{\text{w}}-{\stackrel{\dot{}}{z}}_{\text{b}}\right)-U\\ m_{\text{w}}{\ddot{z}}_{\text{w}}=K_{\text{t}}\left(z_{\text{r}}-z_{\text{w}}\right)-K_{\text{s}}\left(z_{\text{w}}-z_{\text{b}}\right)-C_{\text{s}}\left({\stackrel{\dot{}}{z}}_{\text{w}}-{\stackrel{\dot{}}{z}}_{\text{b}}\right)+U\end{array}$ (1)

Table 1. Parameters of quarter-car model

表1. 1/4车辆模型参数

2.2. 主动悬架预瞄控制方法

假设通过预瞄传感器获得了车辆前方的一段路面信息，它以真实路面高程曲线Q的形式呈现，如图2下方的细实线所示。图2中虚线表示预瞄传感器的探测范围，上方的点划线表示簧载质量垂向位移Q_b，中间的竖向栅格阴影表示悬架动行程，下方的粗实线表示有效路形曲线Q_e。1/4车辆模型的轮胎与路面之间是点接触模型，因此真实路面Q不能直接作为模型的路面输入，而应当是经过轮胎弹性滤波和几何滤波之后的有效路形曲线Q_e [11]。

当簧载质量垂向位移Q_b一直保持为0时，车辆获得最佳平顺性。为此，非簧载质量m_w应主动跟随路面的起伏从而避让路面冲击。当m_w的垂向位移等于有效路形曲线Q_e时，车轮中心跟随Q_e变化，轮胎动载荷为0。此时在预瞄路段内，簧载质量垂向位移 $z_{\text{b}}=Q_{\text{b}}=0$，非簧载质量垂向位移 $z_{\text{w}}=Q_{\text{e}}$，悬架动行程 $z_{\text{w}}-z_{\text{b}}=Q_{\text{e}}-Q_{\text{b}}=Q_{\text{e}}$。将悬架动行程作为被控量，以压缩为正，拉伸为负，使车轮主动避让路面冲击，预瞄路面信息被转换成悬架行程信息。将Q_e作为控制系统的参考信号，令车轮跟随有效路形的起伏而变化，主动退让路面冲击或支撑车身，从而提升车辆的行驶平顺性。

Figure 2. Method of preview control

图2. 预瞄控制方法示意图

3. 有效路形的计算

3.1. 轮胎弹性滚子接触模型

轮胎包容特性是指不平路面对轮胎的垂直作用被轮胎滤波的特性 [11]。轮胎包容特性模型是指轮胎与路面的接触模型，其中弹性滚子接触模型能体现轮胎的弹性滤波和几何滤波效应，其示意图如图3所示。图中的轮心轨迹是这一段不平路面的有效路面输入。本文根据文献 [11] 建立轮胎弹性滚子计算模型。

在实际情况中，悬架受到的垂向激励是经过轮胎滤波后的有效路面输入，因此由预瞄传感器测量得到的路面不平度不能作为悬架将要受到的垂向激励。另一方面，在建立整车模型和天棚阻尼滤波模型时，轮胎与路面的相互作用被简化为点接触弹簧模型。点接触模型适用于路面波长大于3 m，且频率范围是0.1~2 Hz的垂直轴荷的计算 [12]。因此短波长不平路面不能直接输入车辆模型，而应该输入经过轮胎包容特性滤波的有效路面输入。

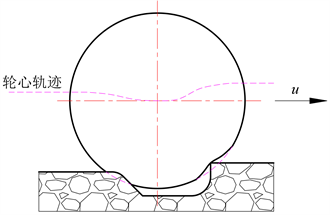
Figure 3. Schematic diagram of tire flexible roller contact model

图3. 轮胎弹性滚子接触模型示意图

3.2. 脉冲输入仿真路面

根据GB/T 4970-2009《汽车平顺性试验方法》中关于脉冲试验用凸块的规定，取等腰三角形凸块长400 mm高40 mm，取矩形凸块长400 mm高40 mm。用弹性滚子模型计算脉冲输入的有效路形如图4所示。经过轮胎包容特性滤波后，三角形凸块的有效路形波峰为32.83 mm，三角形凹坑的波谷为−29.87 mm，矩形凸块对轮胎的纵向作用距离延展为730.0 mm，矩形凹坑则延展为661.0 mm。

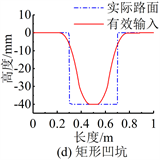
Figure 4. Effective road profile of single impulse input

图4. 单个脉冲输入的有效路形

用以上三角形和矩形构建脉冲输入仿真路面，如图5所示。仿真路面前段是567 mm长的水平路，后接三角形凸块、三角形凹坑、矩形凸块和矩形凹坑，其间隔是1000 mm。最后一段是长9600 mm的水平路面，用来考察控制系统是否稳定。在仿真时输入车辆模型的是有效路形。

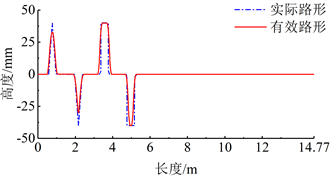
Figure 5. Impulse input simulation road

图5. 脉冲输入仿真路面

3.3. 随机输入仿真路面

悬架平顺性仿真中常用滤波白噪声时域模型来产生路面激励，模拟由路面不平度位移q(t)产生的随机振动：

$\stackrel{\dot{}}{q}\left(t\right)=-2\pi f_{0}q\left(t\right)+2\pi n_0\sqrt{G_{\text{q}}\left(n_0\right)u}\cdot w\left(t\right)$ (2)

式中f₀是下截止时间频率，值为0.01 Hz；n₀是参考空间频率0.1 m⁻¹；G_q(n₀)为路面不平度系数，建立C级路面则取值为256 × 10⁻⁶ m³；u是车速，单位为m/s；w(t)是均值为零且功率谱密度为1的理想单位白噪声信号。设置随机路面的长度为20 m。在仿真时向车辆模型输入经过轮胎弹性滚子接触模型滤波的有效路形。

4. 自抗扰控制器的设计

自抗扰控制器由三个部分组成，分别是跟踪微分器(Tracking Differentiator, TD)、非线性状态误差反馈(Nonlinear State Error Feedback, NLSEF)和扩张状态观测器(Extended State Observer, ESO)。其中TD能快速跟踪控制参考信号，产生一个跟踪信号和一个跟踪微分信号，并能滤除控制参考信号中的噪声。NLSEF根据系统状态误差和状态微分的误差产生控制力。ESO根据系统输出量和控制量，实时估计系统未建模动态、内部扰动和外部扰动，将其视作一个总扰动进行补偿，使被控对象在形式上构成一个积分器串联型系统。

以悬架动行程作为被控量，有效路形曲线Q_e作为控制参考信号，同时Q_e也是1/4车辆模型的路面输入，控制系统的结构如图6所示。图中R是TD的参考输入，v₁和v₂分别是R的跟踪信号和跟踪微分信号。NLSEF-fal是采用fal函数的非线性状态误差反馈，e₁和e₂分别是状态误差和状态微分误差，U₀是反馈控制力。b₀是控制力增益系数，U是系统控制力，y是系统输出。f₀(z₁, z₂)是从1/4车辆模型运动学方程推导的系统已知动态。LESO是线性的ESO，z₁估计y，z₂估计y的微分，z₃估计系统总扰动。

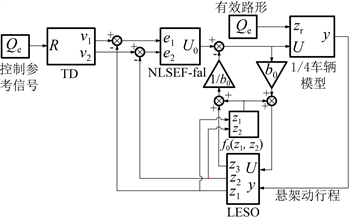
Figure 6. Structure of preview ADRC suspension system

图6. 预瞄ADRC主动悬架系统结构图

4.1. 跟踪微分器

跟踪微分器的连续形式如下：

$\{\begin{array}{l}{\stackrel{\dot{}}{v}}_1=v_2\\ {\stackrel{\dot{}}{v}}_2=fhan\left(v_1-R,v_2,r,h_0\right)\end{array}$ (3)

式中R是参考输入，r是加速度因子，r值越大无超调地跟踪R的速度越快。h₀是滤波因子，其值适当大于仿真步长(离散形式下是计算步长)可以抑制v₂中的噪声放大效应，避免产生高频振荡。fhan是最速控制综合函数， $fhan\left(v_{\text{1}}-ref,v_{\text{2}},h_0\right)$ 的具体形式如下 [13]：

$\{\begin{array}{l}d=r{h}_0^2\\ a_0=h_0{v}_2\\ y=v_1-ref+a_0\\ a_1=\sqrt{d\left(d+8\left|y\right|\right)}\\ a_2=a_0+0.5\text{sign}\left(y\right)\cdot \left(a_1-d\right)\\ a=\left(a_0+y\right)fsg\left(y,d\right)+a_2\left[1-fsg\left(y,d\right)\right]\\ fhan=-r\frac{a}{d}\cdot fsg\left(a,d\right)-r\cdot \text{sign}\left(a\right)\left[1-fsg\left(a,d\right)\right]\end{array}$ (4)

式中sign是符号函数，区间函数fsg的表达式为： $fsg\left(x,d\right)=0.\text{5}\left[\text{sign}\left(x+d\right)-\text{sign}\left(x-d\right)\right]$。

4.2. 非线性状态误差反馈

当选用LESO + PD反馈控制的结构时系统大幅震荡无法稳定，因此NLSEF-fal使用 $fal\left(e,\alpha ,\delta \right)$ 作为非线性增益函数，反馈控制力U₀按下式计算：

$U_0=K_{\text{N1}}\cdot fal\left(e_{\text{1}},{\alpha }_{\text{1}},\delta \right)+K_{\text{N2}}\cdot fal\left(e_{\text{2}},{\alpha }_{\text{2}},\delta \right)$ (5)

$fal\left(e,\alpha ,\delta \right)=\{\begin{array}{l}e÷{\delta }^{1-\alpha }\left|e\right|\le \delta \\ {\left|e\right|}^{\alpha }\cdot \text{sign}\left(e\right)\left|e\right|>\delta \end{array}$ (6)

式(5)中K_N1表示状态误差e₁的反馈增益系数，K_N2表示状态微分误差e₂的反馈增益系数。式(13)中函数fal的自变量依次为状态误差e、非线性指数α和线性区段长度的一半δ。通常取 $0<{\alpha }_{\text{1}}<\text{1}$ 使fal函数对小误差具有大增益，对大误差具有小增益，取 ${\alpha }_{\text{2}}>\text{1}$ 使fal函数对小误差具有小增益，大误差具有大增益。

4.3. 扩张状态观测器

当使用非线性ESO时控制器参数整定困难且容易出现震荡失稳，因此选用LESO。但LESO作为高增益状态观测器，实时估计系统状态的能力不如非线性ESO，因此需根据车辆模型运动学方程将系统已知动态写入LESO，增加其快速性和准确性。否则控制器不能达到控制效果。

将式(5)的第一分式乘以m_w，第二分式乘以m_b，然后相减，整理得到如下表达式：

${\ddot{z}}_{\text{w}}-{\ddot{z}}_{\text{b}}=\frac{K_{\text{t}}}{m_{\text{w}}}\left(z_{\text{r}}-z_{\text{w}}\right)+\frac{m_{\text{b}}+m_{\text{w}}}{m_{\text{b}}{m}_{\text{w}}}U-\frac{m_{\text{b}}+m_{\text{w}}}{m_{\text{b}}{m}_{\text{w}}}\left[K_{\text{s}}\left(z_{\text{w}}-z_{\text{b}}\right)+C_{\text{s}}\left({\stackrel{\dot{}}{z}}_{\text{w}}-{\stackrel{\dot{}}{z}}_{\text{b}}\right)\right]$ (7)

令 $x_1=z_{\text{w}}-z_{\text{b}}$， $x_2={\stackrel{\dot{}}{z}}_{\text{w}}-{\stackrel{\dot{}}{z}}_{\text{b}}$，以悬架动行程作为被控量的二阶系统为：

$\{\begin{array}{l}{\stackrel{\dot{}}{x}}_1=x_2\\ {\stackrel{\dot{}}{x}}_2=f\left[x_1,x_2,t,d\left(t\right)\right]+bU\\ y=x_1\end{array}$ (8)

式中 $f\left[x_1,x_2,t,d\left(t\right)\right]$ 是作用于系统的总扰动，它包含系统状态响应、时变量和外部扰动d(t)。总扰动在形式上分解为已知扰动和未知扰动：

$f\left[x_{\text{1}},x_{\text{2}},t,d\left(t\right)\right]=f_0\left(x_{\text{1}},x_{\text{2}}\right)+f_{\text{1}}\left[x_{\text{1}},x_{\text{2}},t,d\left(t\right)\right]$ (9)

式中 $f_0\left(x_{\text{1}},x_{\text{2}}\right)$ 表示已知扰动，是被控系统的已知动态， $f_{\text{1}}\left[x_{\text{1}},x_{\text{2}},t,d\left(t\right)\right]$ 是系统所受未知扰动。观察式(7)，其第一项代表轮胎对路面输入的响应，实际轮胎与路面的作用比集中刚度点接触模型复杂，将其作为系统未知扰动的一部分；第三项是悬架动行程的动态响应，将其作为系统已知动态，则系统已知动态 $f_0\left(x_{\text{1}},x_{\text{2}}\right)$ 的表达式为：

$f_0\left(x_1,x_2\right)=-\frac{m_{\text{b}}+m_{\text{w}}}{m_{\text{b}}{m}_{\text{w}}}\left(K_{\text{s}}{x}_1+C_{\text{s}}{x}_2\right)$ (10)

将式(7)中U的系数记为b₀，考虑建模有误差， $b_0\ne b$，而 $b_0=\left(m_{\text{b}}+m_{\text{w}}\right)/\left(m_{\text{b}}\cdot m_{\text{w}}\right)$ 是控制力作用于被控对象的已知增益，则作用于二阶系统(8)的控制力 $bU=\left(b-b_0\right)U+b_{0}U$， $\left(b-b_0\right)U$ 是控制力的未知部分。令 $x_{\text{3}}\left(t\right)=f_{\text{1}}\left[x_{\text{1}},x_{\text{2}},t,d\left(t\right)\right]+\left(b-b_0\right)U$，x₃(t)是系统所受总扰动的未知部分，当x₃(t)有界时记 ${\stackrel{\dot{}}{x}}_3=a\left(t\right)$，将x₃(t)扩张为二阶系统(8)的一个状态变量，状态扩张后的系统为：

$\{\begin{array}{l}{\stackrel{\dot{}}{x}}_1=x_2\\ {\stackrel{\dot{}}{x}}_2=x_3+f_0\left(x_1,x_2\right)+b_{0}U\\ {\stackrel{\dot{}}{x}}_3=a\left(t\right)\\ y=x_1\end{array}$ (11)

建立线性扩张状态观测器LESO：

$\{\begin{array}{l}e=z_1-y\\ {\stackrel{\dot{}}{z}}_1=z_2-{\beta }_{1}e\\ {\stackrel{\dot{}}{z}}_2=z_3+f_0\left(z_1,z_2\right)-{\beta }_{2}e+b_{0}U\\ {\stackrel{\dot{}}{z}}_3=-{\beta }_{3}e\end{array}$ (12)

式中z₁、z₂和z₃分别估计系统状态x₁、x₂和x₃，β₁、β₂和β₃是LESO的增益系数，影响观测器的估计能力。用带宽法确定这三个关键控制参数 [14]： ${\beta }_{\text{1}}=\text{3}{\omega }_0$， ${\beta }_{\text{2}}=\text{3}{\omega }_0^2$， ${\beta }_{\text{3}}={\omega }_0^3$，其中ω₀是观测器带宽，其取值影响LESO的快速性和准确性。ω₀的取值与系统的控制能力和被控对象的动态特性有关，是待整定的关键参数。用总扰动的未知部分z₃(t)和系统已知动态f₀(z₁,z₂)实时补偿系统控制力U：

$U=U_0-\left[z_{\text{3}}+f_0\left(z_{\text{1}},z_{\text{2}}\right)\right]÷b_0$ (13)

使用经验法初选所有参数后，再通过仿真试验调整r、K_N1、K_N2和ω₀，得到一组兼顾各个车速下平顺性控制效果的参数，如表2所示。

Table 2. Parameters of preview ADRC

表2. 预瞄ADRC参数表

4.4. 无预瞄线性ADRC

以无预瞄的线性线性自抗扰控制(Linear Active Disturbance Rejection Control, LADRC)主动悬架作为对比。该控制器以簧载质量m_b的垂向位移z_b作为被控量，z_b和控制力U均以铅垂向上为正方向。参考现有文献，参考输入是0，LADRC成为一个位置维持控制器。无预瞄LADRC主动悬架系统如图7所示。

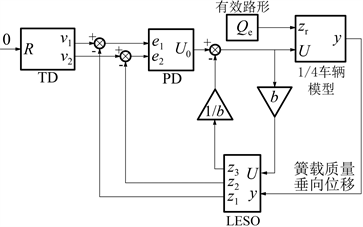
Figure 7. Structure of non-preview ADRC suspension system

图7. 无预瞄LADRC控制系统结构

图中LESO以z_b和U为输入，z₁和z₂分别是z_b和 ${\stackrel{\dot{}}{z}}_{\text{b}}$ 的估计值，z₃估计系统总扰动。TD与式(3)和式(4)保持一致，根据参考输入ref(t)生成跟踪信号v₁和跟踪微分信号v₂。PD是比例微分控制器，以误差e₁和e₂计算反馈控制力U₀，其表达式为：

$U_0=K_{\text{p}}{e}_1+K_{\text{d}}{e}_2$ (14)

式(14)中K_p是比例增益系数，K_d是微分增益系数。LESO的表达式为：

$\{\begin{array}{l}e=z_1-y\\ {\stackrel{\dot{}}{z}}_1=z_2-{\beta }_{1}e\\ {\stackrel{\dot{}}{z}}_2=z_3-{\beta }_{2}e+bU\\ {\stackrel{\dot{}}{z}}_3=-{\beta }_{3}e\end{array}$ (15)

式中β₁、β₂和β₃是LESO的增益系数，同样采用带宽法整定。以z₃补偿系统总扰动形成控制力：

$U=U_0-z_{\text{3}}÷b$ (16)

无预瞄LADRC各部分的参数取值如下：TD速度因子 $r=\text{2}0$，滤波因子 $h_0=0.001$ ；PD比例增益 $K_{\text{p}}=1600$，微分增益 $K_{\text{d}}=\text{8}0$ ；LESO增益 ${\beta }_{\text{1}}=\text{36}0$， ${\beta }_{\text{2}}=\text{432}00$， ${\beta }_3=1728000$ ；控制力增益 $b=0.00\text{28}$。

5. 控制系统仿真

5.1. 脉冲输入路面仿真

建立被动悬架、预瞄ADRC主动悬架和无预瞄LADRC主动悬架仿真模型，输入图5所示的仿真路面。仿真车速为5、10、15···50、55、60 km/h，共12个车速，单次仿真的速度恒定。

仿真结果显示，在5 km/h的低速工况下预瞄ADRC和无预瞄LADRC算法都取得了很好的控制效果，簧载质量垂向加速度均方根值比被动悬架分别减小63.5%和63.12%，如图8所示。随着车速的提高，无预瞄LADRC的减振控制效果迅速减弱，在15 km/h时已经起不到控制效果。而预瞄ADRC所取得的控制效果衰减较慢，从30 km/h开始趋于平缓。以5 km/h和30 km/h的簧载质量垂向加速度时域响应作对比，如图9所示。虽然30 km/h时垂向加速度的均方根值比被动悬架小8.78%，但此时垂向加速度的最大值和最小值与被动悬架的很接近。因此对于脉冲输入路面，预瞄ADRC的最高有效车速为30 km/h。

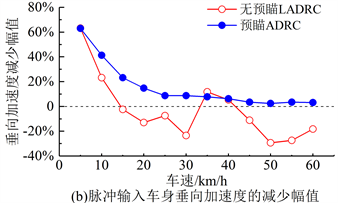
Figure 8. RMS values of sprung mass vertical acceleration of impulse input

图8. 脉冲输入簧载质量垂向加速度均方根值

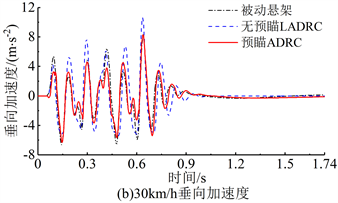
Figure 9. Responds of vertical acceleration of sprung mass under impulse input

图9. 脉冲输入簧载质量垂向加速度的时域响应

考虑运动空间的约束和撞击限位块的概率，悬架行程的最大压缩量需要作为主动悬架系统的约束。如图10所示，被动悬架在20 km/h时出现最大压缩量71.58 mm，预瞄ADRC主动悬架在35 km/h时出现最大压缩量84.68 mm，无预瞄LADRC主动悬架在30 km/h时出现最大压缩量70.68 mm。预瞄ADRC主动悬架由于需要根据有效路形主动避让冲击，因此车轮的运动幅度增大，确实增大了撞击限位块的风险。

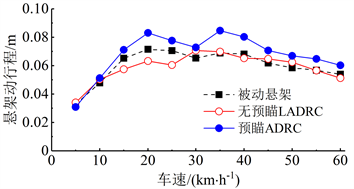
Figure 10. The maximum suspension deflection of impulse input

图10. 脉冲输入下悬架行程最大压缩量

轮胎垂向载荷需要保持稳定，以保证轮胎的抓地力，不使操纵稳定性显著恶化。仿真得到轮胎动载荷均方根值如图11所示，其中预瞄ADRC的均方根值在10 km/h以后始终大于被动悬架。主动悬架的控制作用使轮胎受到更多的垂向压缩载荷。

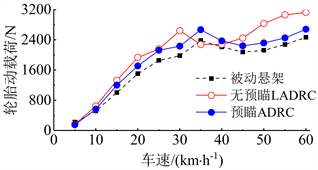
Figure 11. RMS value of tire deflection under impulse input

图11. 脉冲输入轮胎动载荷均方根值

5.2. 随机路面仿真

输入C级路面，仿真车速为5、10、15 $\cdots$ 90、95、100 km/h，共20个车速，单次仿真的速度恒定。各车速下簧载质量垂向加速度均方根值如图12所示。由于随机输入比脉冲输入平缓很多，预瞄ADRC主动悬架的控制效果显著，20 km/h时可使垂向加速度均方根值比被动悬架减少29.79%。而无预瞄的LADRC主动悬架在20 km/h时只能将垂向加速度均方根值减小3.82%，因此无预瞄LADRC的有效车速范围十分有限。在图12(b)中，预瞄ADRC的幅值曲线在50 km/h是最低点，数值为12.09%，此后缓慢上升，在80 km/h值为16.71%，最后在100 km/h值为8.76%。

取5、50 km/h车速下垂向加速度的时域响应，如图13所示。由于无预瞄LADRC从20 km/h起已无控制效果，因此其时域响应不参与对比。随着车速的提高，加速度响应值变大，主、被动悬架的加速度峰值越来越接近，控制效果逐渐减弱。在所有仿真车速下，预瞄ADRC系统的加速度最大值都小于被动悬架，当车速大于50 km/h时，加速度的峰值超过了被动悬架。因此，随机输入下预瞄ADRC系统的有效车速截至50 km/h。

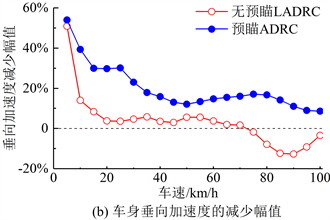
Figure 12. RMS values of sprung mass vertical acceleration of impulse input

图12. 脉冲输入簧载质量垂向加速度均方根值

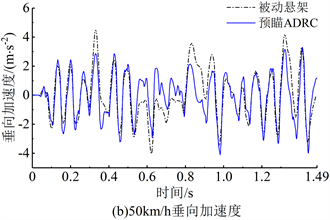
Figure 13. Responds of vertical acceleration of sprung mass under random input

图13. 脉冲输入簧载质量垂向加速度的时域响应

被动悬架和预瞄ADRC主动悬架都在30 km/h时出现悬架行程的最大压缩量，分别是59.98 mm和54.39 mm，如图14所示。随机输入比脉冲输入平缓，两种悬架的车轮最大跳动量接近，因此不会显著增加撞击限位块的风险。随机路面条件下轮胎动载荷的均方根值如图15所示。预瞄ADRC的控制作用增加了轮胎动载荷的均方根值，进而影响了轮胎的接地稳定性，但是未产生显著的恶化。

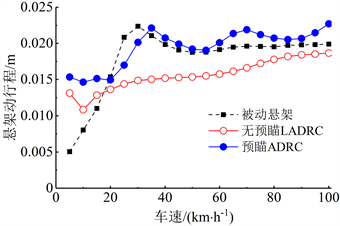
Figure 14. RMS values of suspension deflection under random input

图14. 脉冲输入下悬架行程最大压缩量

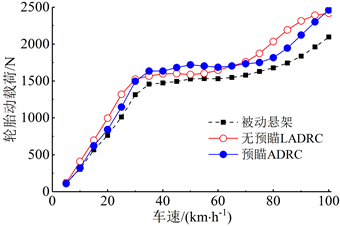
Figure 15. RMS value of tire deflection under random input

图15. 随机输入轮胎动载荷均方根值

6. 结论

本文提出一种以悬架动行程为被控量的预瞄主动悬架控制方法，并以1/4车辆模型为研究对象设计了自抗扰控制器。该预瞄控制方法使用轮胎包容特性弹性滚子接触模型计算预瞄路面的有效路形，并将其作为悬架动行程的控制参考信号。脉冲输入路面和随机路面的仿真计算结果表明，本文所设计的控制系统能够有效减少车身的振动加速度。其中脉冲输入路面的最高有效车速为30 km/h，而随机路面的最高有效车速为50 km/h。该控制系统以同一组参数适应了不同的车速，验证了预瞄控制方法的有效性。

基金项目

广西科技基地和人才专项项目(AD19110019)；广西创新驱动发展专项(AA18242045-3)；广西教育厅科研项目(2018KY0024)；广西制造系统与先进制造技术重点实验室项目(19-050-44-S004)。

NOTES

^*第一作者。

^#通讯作者。