顾客满意指数分析方法研究若干进展

Some Advances in Research of Analysis Method for Customer Satisfaction Index

摘要: 顾客满意指数(CSI)模型属于社会心理学范畴，需要根据观测样本进行测度计量，但是由于模型属于不确定性方程组，已有的算法和公式存在一些问题需要解决：CSI模型的偏最小二乘(PLS)算法不一定收敛,或者收敛速度太慢；一些文献给出的CSI最后计算公式有的缺乏统计稳健性，有的不够全面；现实工作提出了多层顾客满意指数模型问题，需要给出算法。本文介绍我们所在课题组在这些方面的研究所取得的成果：找到了PLS最佳迭代初值，极大提高了收敛速度；进一步给出了基于最小二乘和配方回归的CSI模型的确定性算法；给出了稳健而全面的CSI最终计算公式；给出了多层满意指数模型算法。成果已经在一些单位使用推广。

Abstract: The Customer Satisfaction Index (CSI) model belongs to the category of social psychology and needs to be measured based on observation samples. However, because the model belongs to the uncertainty equation system, there are some problems with existing algorithms and formulas that need to be solved. Partial least square (PLS) algorithm of CSI model does not convergence certainly or its convergence rate is too slow. Some papers offer the last formulae for CSI but which is not robust or not comprehensive. In actual work, the multi-layer CSI model and multi-group CSI model are proposed, but there are not suitable algorithms for them so far. This article introduces the achievements of our research group in these aspects: finding the best iterative initial value, enhancing the convergence rate, further more giving a definite algorithm; giving a suitable and comprehensive formula of CSI, giving suitable algorithms for multi-layer CSI model and multi-group CSI model. Our results have been used in many enterprises.

1. 顾客满意度模型与协方差拟合算法和偏最小二乘算法

Customer Satisfaction Index，简称CSI，上世纪九十年代传入我国以后被翻译做顾客满意度，顾名思义，就是研究顾客对于商品和服务满意的程度。满意与否与满意程度，属于心理活动与心理映射的结果，因此它应该属于社会心理学范畴。该模型被Fornel教授提出 [1] 以后，其测度计量方法研究在不断深入，其应用日益广泛。使得这个模型生机勃勃的原因是，它的指标汇总系数不是事先指定的，而是根据观测样本去临时计算这些系数。这就给统计学提出了新的理论课题，也给实践注入新的活力。从此这个模型渐渐成为顾客满意度模型的主流和国际的通用模型。随着CSI模型测度与分析进入ISO9000标准，它可能成为社会心理学应用最广泛的范例。今天，人们又进一步提出客户满意度、公众满意度、军队士气的概念，满意度应用范围日渐扩充，从企业领域扩充到政务和一般服务领域，但是其测度方法则大同小异。

我们看一个美国顾客满意度模型(图1)，它是一种结构方程模型(Structural Equation Model) [2]。其中的6个结构变量(隐含变量) ${\xi }_1$ 、 ${\eta }_1~{\eta }_5$ 我们放在上层，它们之间含有9个作用关系，我们用水平的箭头表示。我们要注意区分哪些是自变量，哪些是因变量。只对别的结构变量起作用的是自变量，受到别的结构变量作用的是因变量。在方程组里，因变量作用的关系(实线箭头所示)我们统一使用符号 ${\beta }_{i\text{}j}$ 表示，而对自变量作用的关系我们使用符号 ${\gamma }_1~{\gamma }_3$ 表示，(虚线箭头所示)。

结构方程模型还有一个方程组，就是观测变量要汇总到结构变量，图1中我们把观测变量放在下层，每一个结构变量对应若干个观测变量，它们使用符号 $x_t$ 、 $y_k$ 表示。观测变量要汇总到结构变量，这种关系我们用竖直的箭头表示。假设观测变量一共有N个观测，它们是向量，汇总以后的结构变量也是向量。结构方程组就这样含有两层关系，一个是观测方程组；一个是结构方程组。

图1显示的结构变量之间的关系是如(1)表示的结构方程组。注意因变量之间的作用是互相的，所以第一个矩阵是方阵。图1的模型只含有一个自变量，它一共作用于三个因变量，于是方程组里就有1列。后面的误差是随机的，这是统计模型惯用的表示。

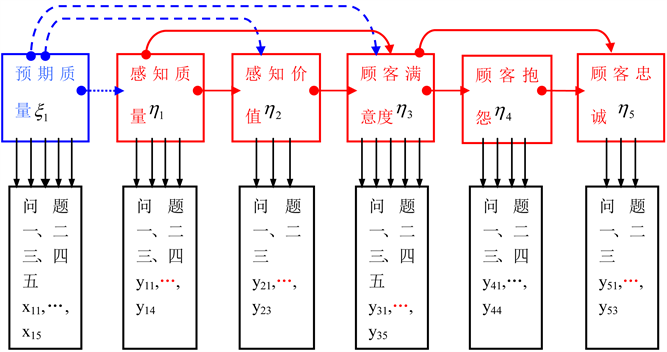
Figure 1. US customer satisfaction index model

图1. 美国顾客满意指数模型

$\left(\begin{array}{c}{\eta }_1\\ {\eta }_2\\ {\eta }_3\\ {\eta }_4\\ {\eta }_5\end{array}\right)=\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ {\beta }_{21}& 0& 0& 0& 0\\ {\beta }_{31}& {\beta }_{32}& 0& 0& 0\\ 0& 0& {\beta }_{43}& 0& 0\\ 0& 0& {\beta }_{53}& {\beta }_{54}& 0\end{array}\right)\left(\begin{array}{c}{\eta }_1\\ {\eta }_2\\ {\eta }_3\\ {\eta }_4\\ {\eta }_5\end{array}\right)+\left(\begin{array}{c}{\gamma }_1\\ {\gamma }_2\\ {\gamma }_3\\ 0\\ 0\end{array}\right){\xi }_1+\left(\begin{array}{c}{\epsilon }_{\eta 1}\\ {\epsilon }_{\eta 2}\\ {\epsilon }_{\eta 3}\\ {\epsilon }_{\eta 4}\\ {\epsilon }_{\eta 5}\end{array}\right)$ (1)

下面我们来讨论观测数据矩阵的维数。对每一个观测变量有N个观测，因此观测数据有N行。设一共有M个观测变量，那么就有M列，这样就形成了一个 $N\times M$ 的观测数据阵。怎么排列观测变量呢？我们按照图1显示的关系排列好了，将各个观测变量按照它们所隶属的结构变量从左到右顺序排列。可以把原始数据矩阵记录在一个Excel表上。

一级指标(结构变量)与二级指标(观测变量)之间存在作用关系与影响关系，表达它们之间的关系，可以有两种互逆的方式。传统的是认为结构变量受对应的观测变量影响，如果观测变量改变了，当然对应的结构变量也就随着改变，正像一个班级的学生参加期末考试，如果某一门成绩或者各门成绩改变了，那么总分就随着改变。但是我们也可以反过来看，为什么各门成绩会不一样呢？还不是因为他们的成绩档次也就是总分不一样？两种看法都有道理，到底使用哪一种，要看解方程的需要。

与结构因变量 ${\eta }_i$ 对应的观测变量以 $y_{i\text{}\text{}j}$ 表示，图1中 $i=1,\cdots ,5$， $j=1,\cdots ,L\left(i\right)$， $L\left(i\right)=4,3,5,4,3$。与结构自变量 ${\xi }_1$ 对应的观测变量以 $x_{t\text{}\text{}j}$ 表示，图1中 $t=1$， $j=1,\cdots ,K\left(t\right)$，并且 $K\left(1\right)=5$。认为观测变量是受结构变量影响的的观测方程组如(2) (3)所示。

$\left(\begin{array}{c}{x}_{t1}\\ ⋮\\ x_{tK\left(t\right)}\end{array}\right)=\left(\begin{array}{c}{\upsilon }_{t1}\\ ⋮\\ {\upsilon }_{tK\left(t\right)}\end{array}\right){\xi }_1+\left(\begin{array}{c}{\epsilon }_{xt1}\\ ⋮\\ {\epsilon }_{xtK\left(t\right)}\end{array}\right)$， $t=1$ (2)

$\left(\begin{array}{c}{y}_{i1}\\ ⋮\\ y_{iL\left(i\right)}\end{array}\right)=\left(\begin{array}{c}{\lambda }_{i1}\\ ⋮\\ {\lambda }_{iL\left(i\right)}\end{array}\right){\eta }_i+\left(\begin{array}{c}{\epsilon }_{yi1}\\ ⋮\\ {\epsilon }_{yiL\left(i\right)}\end{array}\right)$， $i=1,\cdots ,5$ (3)

其中 ${\upsilon }_{tj}$ 、 ${\lambda }_{ij}$ 为载荷项。上面方程的右边是结构变量，左边是观测变量。我们也可以反过来写出观测方程，左边是结构变量，右边是观测变量：

${\xi }_t={\displaystyle \underset{j=1}{\overset{K\left(t\right)}{\sum }}{\psi }_{t\text{}\text{}j}{x}_{t\text{}\text{}j}}+{\epsilon }_{xt}$， $t=1$ (4)

${\eta }_i={\displaystyle \underset{j=1}{\overset{L\left(i\right)}{\sum }}{\omega }_{i\text{}\text{}j}{y}_{i\text{}\text{}j}}+{\epsilon }_{\eta i}$， $i=1,\cdots ,5$ (5)

我们采用矩阵记法来一般描述结构方程组(1)。作为结构方程一般的系数矩阵，对角线表示的是自己对自己的作用，当然是0。一般的结构方程模型各个结构变量之间的作用可以安排从前到后，此时系数矩阵就是下三角矩阵。但是也有一些结构方程模型结构变量之间出现互相的作用，此时其系数矩阵可以不是下三角的。这种情况在我们的DASC软件里也可以计算。设结构方程组(1)含有k + m个结构变量，其中k个自变量，m个因变量，将(1)左边的向量记作记 $\eta$，右边 $\eta$ 的系数矩阵记为B，它是m阶方阵。方程组(1)的右边的自变量记作 $\xi$， $\xi$ 的系数矩阵为 $m\times k$ 阶矩阵，记为 $\Gamma$，则结构方程组(1)可以扩展为：

$\eta =B\eta +\Gamma \xi +{\epsilon }_{\eta }$ (6)

其中残差向量为 ${{\epsilon }^{\prime }}_{\eta }=\left({{\epsilon }^{\prime }}_1,\cdots ,{{\epsilon }^{\prime }}_m\right)$。

类似地记观测向量 ${x^{\prime }}_t=\left({x^{\prime }}_{t1},\cdots ,{x^{\prime }}_{tS\left(t\right)}\right)$， $t=1,\cdots ,k$， $S\left(t\right)$ 是与第t个结构自变量相联系的观测变量个数，记 ${y^{\prime }}_i=\left({y^{\prime }}_{i1},\cdots ,{y^{\prime }}_{iL\left(i\right)}\right)$， $i=1,\cdots ,m$ ；记 ${{\upsilon }^{\prime }}_t=\left({{\upsilon }^{\prime }}_{t1},\cdots ,{{\upsilon }^{\prime }}_{tS\left(t\right)}\right)$， ${{\lambda }^{\prime }}_i=\left({{\lambda }^{\prime }}_{i1},\cdots ,{{\lambda }^{\prime }}_{iL\left(i\right)}\right)$，则观测方程组(2)可以扩展为：

$x_t={\upsilon }_t{\xi }_t+{\epsilon }_{xt}$， $t=1,\cdots ,k$ (7)

(3)可以扩展为：

$y_i={\lambda }_i{\eta }_i+{\epsilon }_{yi}$， $i=1,\cdots ,m$ (8)

采用矩阵记法，令 $X^{\prime }=\left({x^{\prime }}_1,\cdots ,{x^{\prime }}_k\right)$， ${\Lambda }_X=I_k\otimes {\upsilon }_t$， ${{\epsilon }^{\prime }}_X=\left({{\epsilon }^{\prime }}_{x1},\cdots ,{{\epsilon }^{\prime }}_{xk}\right)$， $Y^{\prime }=\left({y^{\prime }}_1,\cdots ,{y^{\prime }}_m\right)$， ${\Lambda }_Y=I_m\otimes {\lambda }_i$， ${{\epsilon }^{\prime }}_Y=\left({{\epsilon }^{\prime }}_{y1},\cdots ,{{\epsilon }^{\prime }}_{ym}\right)$，其中I是单位方阵，则(7)(8)可以表为：

$X={\Lambda }_X\xi +{\epsilon }_X$ (9)

$Y={\Lambda }_Y\eta +{\epsilon }_Y$ (10)

记 ${{\psi }^{\prime }}_t=\left({{\psi }^{\prime }}_{t1},\cdots ,{{\psi }^{\prime }}_{tS\left(t\right)}\right)$， ${{\omega }^{\prime }}_i=\left({{\omega }^{\prime }}_{i1},\cdots ,{{\omega }^{\prime }}_{iL\left(i\right)}\right)$，令 $\psi =I_k\otimes {\psi }_t$， $\omega =I_m\otimes {\omega }_i$，则(4)、(5)可以记为：

$\xi =\psi X+{\epsilon }_{\xi }$ (11)

$\eta =\omega Y+{\epsilon }_{\eta }$ (12)

(6)、(7)、(8)合在一起组成了结构方程模型或者路径分析模型，类似的(6)、(11)、(12)也是如此。它们在心理学领域和其它领域都有广泛的应用 [3] [4] [5]。

SEM中只有观测变量已知，其余都是未知，就是说，在方程(4-5)或者(11-12)中只有右边的变量已知，其余的方程系数和方程左边的变量都未知，因此它属于不确定方程组，计算结果是不唯一的，同时算法也不止一个。目前主要流行算法有两个：偏最小二乘法(Partial Least Square, PLS) [6] [7] 与协方差拟合法(Linear Structure RELationship, LISREL)。

协方差拟合法(LISREL)的基本思想是认为样本协方差阵应该与模型协方差阵如出一辙，应该近似相等。而矩阵与矩阵相等就是矩阵的每个元素对应相等，于是矩阵有多少元素就可以得到多少方程等式，从而求得模型的参数估计。这个算法对样本容量和分布的要求严格，即使数据相同，仅仅分布假设不一样，计算结果会完全不同，所以很少在实际工作中使用。

偏最小二乘法(PLS)的基本思想是先赋予一组结构变量的初值，它就变成已知的了。于是可以求解各个方程组里的系数。有了系数的估计，又可以根据观测变量的数据求得结构变量的估计值。现在的结构变量就不再是任给的初值了，而是第一次迭代求得的解。于是又可以求得系数的估计值，又可以根据观测变量初值求得结构变量第二次的估计值。如此循环迭代下去，每一步都计算两次迭代结果的误差，如果误差小于某一个事先指定的小数字，就停止迭代。显然这是一种典型的不确定性迭代算法，简明实用，但是不一定能保证其迭代收敛性，收敛速度也可能太慢。同一个模型中，即使相同的数据，仅仅只是迭代精度不同，也可能得到完全不同的结果。这样就使得计算不具备可比较性。特别是，迭代初值对迭代结果有很大影响。那么什么是最佳的迭代初值呢？

2. 偏最小二乘算法的最佳迭代初值

前面分析了结构方程模型是不确定方程组，一般的最小二乘解并不唯一。怎么办呢？我们可以加上一些约束来求解。

我们先讨论模型解的一些基本性质。作为不定方程，它的解并不唯一，可以相差一个常数倍。这从方程两边都含有同一变量的线性组合即可得知。也就是说，若 $\eta$ 是一组解，则 $c\eta$ 也是一组解；类似的，若 $\xi$ 是一组解，则 $c\xi$ 也是一组解，这里c是任一不为0的常数。所谓向量相差常数倍，就是方向不变而模长发生变化，于是我们可以在 ${\xi }_i$ 、 ${\eta }_i$ 为单位向量的条件下求解。同时我们还注意到，方程(3)和(5)在 ${\displaystyle \underset{j=1}{\overset{L\left(i\right)}{\sum }}{\omega }_{i\text{}\text{}j}{\lambda }_{i\text{}\text{}j}}=1$ 的条件下等价，因而(3)的最小二乘解也就是(5)的最小二乘解。

灵活运用上述性质，有助于我们找到PLS的最佳迭代初值和SEM的确定性算法 [8]。

方程(2)或(3)不仅是不确定方程组而且是矛盾方程组，即一个结构变量要同时满足与多个观测变量的线性关系。矛盾方程组应该使用最小二乘法则，找到最小二乘解。将第i个结构向量与其对应的观测向量的第s个分量应该满足的关系写出来就是：

$y_{ijs}={\lambda }_{ij}{\eta }_{is}$， $j=1,2,\cdots ,L\left(i\right)$， $s=1,2,\cdots ,N$ (13)

在多元线性回归模型里，如果因变量是未知的，几何意义是一个任意向量到一个子空间的距离，这意味着有无穷多组解。现在我们根据模型性质假定因变量的模长为1，于是问题理解为求一个单位球面到一个线性子空间的距离，这是可以求解的。

为了有利于编程，我们还可以更简捷推导出解的表达式。对于(8)，将 $y_i$ 转置与自己作乘积 $y_i{y^{\prime }}_i\approx {\lambda }_i{\eta }_i{{\eta }^{\prime }}_i{{\lambda }^{\prime }}_i={\eta }_i{{\eta }^{\prime }}_i{\lambda }_i{{\lambda }^{\prime }}_i$，这里观测变量 $y_i$ 是 $L\left(i\right)\times N$ 矩阵。如果取结构变量为单位向量，即 ${\eta }_i{{\eta }^{\prime }}_i=1$，则有 $y_i{y^{\prime }}_i\approx {\lambda }_i{{\lambda }^{\prime }}_i$。这是两个 $L\left(i\right)\times L\left(i\right)$ 的矩阵在最小二乘意义下的近似相等，详细写出就是：

$\left(\begin{array}{cccc}{y}_{i1}{y^{\prime }}_{i1}& y_{i1}{y^{\prime }}_{i2}& \cdots & y_{i1}{y^{\prime }}_{iL\left(i\right)}\\ y_{i2}{y^{\prime }}_{i1}& y_{i2}{y^{\prime }}_{i2}& \cdots & y_{i2}{y^{\prime }}_{iL\left(i\right)}\\ ⋮& ⋮& \ddots & ⋮\\ y_{iL\left(i\right)}{y^{\prime }}_{i1}& y_{iL\left(i\right)}{y^{\prime }}_{i2}& \cdots & y_{iL\left(i\right)}{y^{\prime }}_{iL\left(i\right)}\end{array}\right)\approx \left(\begin{array}{cccc}{\lambda }_{i1}^2& {\lambda }_{i1}{\lambda }_{i2}& \cdots & {\lambda }_{i1}{\lambda }_{iL\left(i\right)}\\ {\lambda }_{i2}{\lambda }_{i1}& {\lambda }_{i2}^2& \cdots & {\lambda }_{i2}{\lambda }_{iL\left(i\right)}\\ ⋮& ⋮& \ddots & ⋮\\ {\lambda }_{iL\left(i\right)}{\lambda }_{i1}& {\lambda }_{iL\left(i\right)}{\lambda }_{i2}& \cdots & {\lambda }_{iL\left(i\right)}^2\end{array}\right)$ (14)

上面左边矩阵的元素是两个向量相乘得到的数，右边的元素是数与数相乘得到的数。取对角线的元素相等，即得：

${\lambda }_{ik}^2=y_{ik}{y^{\prime }}_{ik}$， $k=1,\cdots ,L\left(i\right)$ (15)

对于自变量 ${\xi }_t$ 也有类似结果。这样我们得到了向量 ${\lambda }_i$ 的估计值 ${\hat{\lambda }}_i={\left({\hat{\lambda }}_{i1},\cdots ,{\hat{\lambda }}_{iL\left(i\right)}\right)}^{\prime }$，它是观测变量与结构变量之间的系数的最小二乘意义下的解。

有了系数的估计值，我们再来估计结构变量 ${\eta }_i$。已设 ${\eta }_i={\left({\eta }_{i1},{\eta }_{i2},\cdots ,{\eta }_{iN}\right)}^{\prime }$，我们要逐个估计它的分量。将(13)写成向量形式就是

$\left(\begin{array}{c}{y}_{i1s}\\ ⋮\\ y_{iL\left(i\right)s}\end{array}\right)\approx \left(\begin{array}{c}{\lambda }_{i1}\\ ⋮\\ {\lambda }_{iL\left(i\right)}\end{array}\right){\eta }_{is}$， $s=1,\cdots ,N$ (16)

根据最小二乘原理，我们又可以获得 ${\eta }_{is}$ 的最小二乘估计：

${\lambda }_i{{\lambda }^{\prime }}_i{\eta }_{is}={\displaystyle \underset{k=1}{\overset{L\left(i\right)}{\sum }}{\lambda }_{ik}^2{\eta }_{is}}=\left({\lambda }_{i1},\cdots ,{\lambda }_{iL\left(i\right)}\right)\left(\begin{array}{c}{y}_{i1s}\\ ⋮\\ y_{iL\left(i\right)s}\end{array}\right)={{\lambda }^{\prime }}_i{Y}_s$ (17)

${\hat{\eta }}_{is}=\frac{{\widehat{{\lambda }^{\prime }}}_i{Y}_s}{{\hat{\lambda }}_i{{\hat{\lambda }}^{\prime }}_i}$， $s=1,\cdots ,N$ (18)

这里的 ${\hat{\lambda }}_i$ 是已经估计出来的值。类似我们可以估计出 ${\upsilon }_{t\text{}\text{}j}$ 与 ${\xi }_t$。这样我们得到了全部结构变量在模长单位向量约束下的最小二乘解(MCLS)，它满足

$\Vert {\eta }_i-{\displaystyle \underset{j=1}{\overset{L\left(i\right)}{\sum }}{\omega }_{i\text{}\text{}j}{y}_{i\text{}\text{}j}}\Vert \to \min$ (19)

其几何意义是求一个单位球面与一个子空间(超平面)的距离 [9]。

回到结构方程组(2)，现在我们已经有了观测方程组的最小二乘解 ${\hat{\xi }}_t,{\hat{\eta }}_i$，于是(2)成为一个普通方程组，可以求得它的最小二乘方法解。如果我们继续采用PLS算法，将不是任取迭代初值，而是采用我们的MCLS计算结果作为迭代初值，因为MCLS已经在最小二乘意义下满足了一个方程组，显然收敛速度就快得多。在一个250份普通样本的计算中，相对于传统的PLS算法，我们的新算法可以提高收敛速度数百倍。

还可以讨论MCLS的无偏性问题，这里省略。

3. SEM基于最小二乘和配方约束的确定性算法

这一节我们继续探索，寻找更合适的约束条件来求解SEM这个不确定方程组。

首先介绍配方条件和配方约束 [10]。配方条件就是各个加权系数之和为1，且都非负。如果要求路径系数满足配方条件，就是配方约束，这在实际工作中是合理的。例如高考各科分数加总分，如果总分与各科分数都要求是百分制，那么加权系数之和必须为1。在方程(4) (5)中，也就是满足

${\displaystyle \underset{j=1}{\overset{K\left(i\right)}{\sum }}{\psi }_{i\text{}\text{}j}=1}$， ${\psi }_{i\text{}\text{}j}\ge 0$ (20)

${\displaystyle \underset{j=1}{\overset{L\left(i\right)}{\sum }}{\omega }_{i\text{}\text{}j}=1}$， ${\omega }_{i\text{}\text{}j}\ge 0$ (21)

配方条件的计算主要有两种情况。

如果根据最佳迭代初值计算出来的MCLS的相应路径系数都是正数，只是其和不为1，那么很简单，设系数之和为c，那么在方程(4) (5)中两边同时除以c就可以了，得出的各个路径系数之和肯定为1。

如果开始时MCLS的相应路径系数计算结果含有负数，完全照搬方开泰教授提出的配方回归的方法 [11] [12] 是行不通的，因为我们这里只是知道回归因向量的方向，模长是初始设定为1，我们可以对模长拉伸压缩，保持方向不变，同时照样去掉负系数的自变量。剩余的回归方程的自变量少了一些，非负，但是其和未必为1，一般大于1。因为原来包括有负系数的系数之和为1，去掉负数以后其和就大于1了，不妨设为c。再在方程(4) (5)中两边同时除以这个c，如同上段讨论的那样。

当然实际工作中把辛辛苦苦得到的观测变量完全去掉可能并不合适，我们可以将配方条件改为 ${\psi }_{i\text{}\text{}j}\ge \delta$ 和 ${\omega }_{i\text{}\text{}j}\ge \delta$，这里 $\delta$ 是某一小的正数。如果初始回归系数有小于 $\delta$ 的，一律改为 $\delta$，这样就避免了生硬的去掉变量。剩下的问题是怎么样使得回归系数之和为1，这个不难，可以参照上面介绍的方法。在DASC软件里，只需设定一下即可。

结构方程模型里的第一步，将观测变量汇总到各自对应的结构变量，这和学生期末考试各科成绩加总分是一回事情。所不同的是，日常考试时加总分的加权系数是事先已知的，而结构方程模型里的加权系数是根据样本临时计算的。

采用配方约束来做观测变量的汇总是非常合理的，可以保证汇总的指标与观测变量指标取值范围相同。

我们的算法包括两个阶段，开始对结构变量的单位向量约束只是一个过渡阶段，然后对路径系数的配方约束才是确定性算法的最终结果，当然自始至终要遵循最小二乘原理。

4. 顾客满意度的最后计算公式

考虑顾客满意度的常用计算公式，都是把数据的最大值最小值作为单项参与计算，这就不符合统计稳健性要求。

$\text{CSI}=\frac{E\left(\xi \right)-\min \left(\xi \right)}{\max \left(\xi \right)-\min \left(\xi \right)}$， $\max \left(\xi \right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\omega }_i\max \left(X_i\right)}$， $\min \left(\xi \right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\omega }_i\min \left(X_i\right)}$ (22)

有的文献提出使用如下公式：

$\text{CSI}={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\omega }_i{X}_i}/{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\omega }_i}$

这个公式是稳健了，但是它没有考虑其它结构变量对应的观测变量的影响，因而不够全面。

我们建议CSI最终计算公式为：

$\text{CSI}=\frac{{\displaystyle \underset{t=1}{\overset{k}{\sum }}{\displaystyle \underset{j=1}{\overset{S\left(t\right)}{\sum }}{\psi }_{t\text{}j}{\gamma }_{i_{0}t}{\bar{x}}_{t\text{}j}}+{\displaystyle \underset{i=1}{\overset{i_0}{\sum }}{\displaystyle \underset{j=1}{\overset{L\left(i_0\right)}{\sum }}{\omega }_{i\text{}j}{\beta }_{i0i}{\bar{y}}_{i\text{}j}}+{\displaystyle \underset{j=1}{\overset{L\left(i_0\right)}{\sum }}{\omega }_{i_{0}j}{\bar{y}}_{i_{0}j}}}}}{{\displaystyle \underset{t=1}{\overset{k}{\sum }}{\displaystyle \underset{j=1}{\overset{S\left(t\right)}{\sum }}{\psi }_{t\text{}j}{\gamma }_{i_{0}t}}+{\displaystyle \underset{i=1}{\overset{i_0}{\sum }}{\displaystyle \underset{j=1}{\overset{L\left(i_0\right)}{\sum }}{\omega }_{i\text{}j}{\beta }_{i_{0}i}}+{\displaystyle \underset{j=1}{\overset{L\left(i_0\right)}{\sum }}{\omega }_{i_{0}j}}}}}$ (23)

这个公式有些繁琐，但是脉络是清楚的。 ${\eta }_{i0}$ 是顾客满意度变量， $i_0$ 是顾客满意度变量的结构变量编号。

5. 多层顾客满意度模型及其算法

实际工作可能遇到这样的情况，一级指标或者结构变量先派生出若干个低层次的结构变量，再让这些低层次的结构变量与观测变量相联系。这就提出了多层路径分析模型，如图2所示。

图2是一个多层的中国顾客满意度模型，含有多层结构变量，如何写出其结构方程是解决问题的关键。我们知道，利用结构方程模型解决顾客满意度问题，一般先是画出模型图示，再分析其结构，确定模型的基本框架。一旦这个清楚了，就可以写出对应的方程，确定其算法，利用现成的软件计算出结果。图2的关键是如何理解和处理派生的低层次结构变量。我们发现可以将派生的低层次的结构变量理解为结构自变量，它们也以 ${\xi }_i$ 标记。于是我们找到了解决问题的关键，模型思路就豁然开朗了。

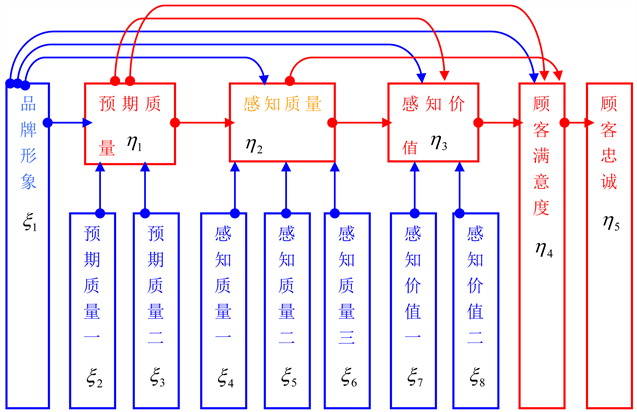
Figure 2. A multi-layered Chinese customer satisfaction model

图2. 一个多层的中国顾客满意度模型

这个模型的基本结构方程如(24)：

$\left(\begin{array}{c}{\eta }_1\\ {\eta }_2\\ {\eta }_3\\ {\eta }_4\\ {\eta }_5\end{array}\right)=\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ {\beta }_{21}& 0& 0& 0& 0\\ {\beta }_{31}& {\beta }_{32}& 0& 0& 0\\ {\beta }_{41}& {\beta }_{42}& {\beta }_{43}& 0& 0\\ 0& 0& 0& {\beta }_{54}& 0\end{array}\right)\left(\begin{array}{c}{\eta }_1\\ {\eta }_2\\ {\eta }_3\\ {\eta }_4\\ {\eta }_5\end{array}\right)+\left(\begin{array}{cccccccc}{\gamma }_{11}& {\gamma }_{12}& {\gamma }_{13}& 0& 0& 0& 0& 0\\ {\gamma }_{21}& 0& 0& {\gamma }_{24}& {\gamma }_{25}& {\gamma }_{26}& 0& 0\\ {\gamma }_{31}& 0& 0& 0& 0& 0& {\gamma }_{37}& {\gamma }_{38}\\ {\gamma }_{41}& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right)\left(\begin{array}{c}{\xi }_1\\ {\xi }_2\\ ⋮\\ {\xi }_7\\ {\xi }_8\end{array}\right)+\left(\begin{array}{c}{\epsilon }_{\eta 1}\\ {\epsilon }_{\eta 2}\\ {\epsilon }_{\eta 3}\\ {\epsilon }_{\eta 4}\\ {\epsilon }_{\eta 5}\end{array}\right)$ (24)

结构自变量对应的观测方程方程为(25)：

$\left(\begin{array}{c}{x}_{t1}\\ ⋮\\ x_{tS\left(t\right)}\end{array}\right)=\left(\begin{array}{c}{\upsilon }_{t1}\\ ⋮\\ {\upsilon }_{tS\left(t\right)}\end{array}\right){\xi }_t+\left(\begin{array}{c}{\epsilon }_{xt1}\\ ⋮\\ {\epsilon }_{xtS\left(t\right)}\end{array}\right)$， $t=1,\cdots ,8$ (25)

在一个算例里 $S\left(t\right)$ 分别为5，4，3，2，5，4，3，2；同时 ${\eta }_4,{\eta }_5$ 分别与4个观测变量相联系，则结构因变量对应的观测方程为(26)：

$\left(\begin{array}{c}{y}_1\\ ⋮\\ y_4\\ y_5\\ ⋮\\ y_8\end{array}\right)=\left(\begin{array}{cc}{\lambda }_{11}& 0\\ ⋮& 0\\ {\lambda }_{41}& 0\\ 0& {\lambda }_{12}\\ 0& ⋮\\ 0& {\lambda }_{42}\end{array}\right)\left(\begin{array}{c}{\eta }_4\\ {\eta }_5\end{array}\right)+\left(\begin{array}{c}{\epsilon }_{y1}\\ ⋮\\ {\epsilon }_{y4}\\ {\epsilon }_{y5}\\ ⋮\\ {\epsilon }_{y8}\end{array}\right)$ (26)

高层次结构因变量与低层次结构自变量关系方程为(27)：

$\left(\begin{array}{c}{\xi }_2\\ {\xi }_3\\ {\xi }_4\\ {\xi }_5\\ {\xi }_6\\ {\xi }_7\\ {\xi }_8\end{array}\right)=\left(\begin{array}{ccc}{\alpha }_{11}& 0& 0\\ {\alpha }_{21}& 0& 0\\ 0& {\alpha }_{12}& 0\\ 0& {\alpha }_{22}& 0\\ 0& {\alpha }_{32}& 0\\ 0& 0& {\alpha }_{13}\\ 0& 0& {\alpha }_{23}\end{array}\right)\left(\begin{array}{c}{\eta }_1\\ {\eta }_2\\ {\eta }_3\end{array}\right)+\left(\begin{array}{c}{\epsilon }_{\xi 2}\\ {\epsilon }_{\xi 3}\\ {\epsilon }_{\xi 4}\\ {\epsilon }_{\xi 5}\\ {\epsilon }_{\xi 6}\\ {\epsilon }_{\xi 7}\\ {\epsilon }_{\xi 8}\end{array}\right)$ (27)

其中 ${\mu }_{i\text{}\text{}j},{\lambda }_{i\text{}\text{}j},{\alpha }_{i\text{}\text{}j}$ 为载荷项， ${\epsilon }_i$ 为误差项。

于是多层结构方程模型问题就迎刃而解了，包括模型的描述，方程组的表达，然后就可以类似于前面的分析，作出它的基于单位向量约束下的最小二乘解，给出确定性算法。虽然路径系数的计算要复杂一些，变量编号查找与属性判定也比较复杂，但是那只是软件编程问题，软件DASC完全可以解决。

NOTES

^*通讯作者。