分数布朗运动的指数泛函

The Exponential Functional of Fractional Brownian Motion

摘要: 本文旨在研究分数布朗运动指数泛函∫₀^te^σB_sH-μsds,σ∈R,μ>0，Hurst指数H∈(1/2,1)的离散化与分布问题。

Abstract: In this note, we will investigate the discrete approximations and the characteristic function of the exponential functional of fractional Brownian motion ∫₀^te^σB_sH-μsds,σ∈R,μ>0 with Hurst index H∈(1/2,1).

1. 引言

在数理金融方面，具有漂移项的布朗运动的指数泛函的相关内容被广泛研究，如著名的Black-Scholes模型，特别是亚式期权的定价问题等价于指数泛函的分布问题，这一问题已主要被Dufresne [1] [2] [3] [4]，Marc-Yor [5] 和Tamas Szabados [6] [7] 解决。主要有以下几个结果：

1. (Dufresne, 1989) $A_t^{\mu }={\displaystyle {\int }_0^t{\text{e}}^{2\mu s+2W_s}\text{d}s},t\ge 0,\mu \in R,a_k=k\mu +k^2,n=0,1,2,\cdots$

$E{\left(2A_t^{\mu }\right)}^n=n!{\displaystyle \underset{k=0}{\overset{n}{\sum }}{\text{e}}^{2{\alpha }_{k}t}}{\left[{\displaystyle \underset{\begin{array}{l}j=0\\ j\ne k\end{array}}{\prod }\left({\alpha }_k-{\alpha }_j\right)}\right]}^{-1}$

2. (Dufresne, 1990)对任意 $\mu >0$， $\frac{1}{A_{\infty }^{\left(-\mu \right)}}~\Gamma \left(\mu ,1\right)$，其中 $\Gamma \left(,\right)$ 为伽马分布

3. (Yor, 1992a) $A_t^{\mu }={\displaystyle {\int }_0^t{\text{e}}^{2\mu \tau +2B\tau }}\text{d}\tau ,t\ge 0,\mu \in R$

4. (Yor, 1992c)

$P\left(A_t^{\mu }\in \text{d}u|B_t+\mu t=x\right)=a_t\left(x,u\right)\text{d}u=\frac{\sqrt{2\pi t}}{\mu }\exp \left(\frac{x^2}{2t}-\frac{1}{2\mu }\left(1+{\text{e}}^{2x}\right)\right){\theta }_{{\text{e}}^x/\mu }\left(t\right)\text{d}u$

其中 ${\theta }_r\left(t\right)=\frac{r}{\sqrt{2{\pi }^{3}t}}\exp \left(\frac{{\pi }^2}{2t}\right){\displaystyle {\int }_0^{\infty }\text{d}y\exp \left(-y^2/2t\right)\exp \left(-r\cosh y\right)\left(\sinh y\right)\sin \left(\frac{\pi y}{t}\right)}$。

但大量的金融实证表明，金融资产的收益率呈现出尖峰厚尾的分布特点，且资产价格呈现出长相关性，这并不符合布朗运动的特性。分数布朗运动驱动的随机微分方程来描述资产价格变化过程更加符合实际，但由于分数布朗运动既不是马尔科夫过程，又不是半鞅，所以不能用标准布朗运动的随机计算理论来研究股票价格的演化过程。为使分数布朗运动理论能够顺利地应用于金融市场，建立了分数路径依赖型积分(fractional pathwise integral)和分数型Wick-Ito型积分。

本文我们将布朗运动的指数泛函问题推广至分数布朗运动。考虑 ${\displaystyle {\int }_0^t{\text{e}}^{\sigma B_s^H-\mu s}}\text{d}s$，其中 $B_s^H$ 为Hurst指数 $H\in \left(\frac{1}{2},1\right)$ 的分数布朗运动。我们定义 $U_t={\text{e}}^{\sigma B_t^H-\mu t},A_t={\displaystyle {\int }_0^t{\text{e}}^{\sigma B_s^H-\mu s}}\text{d}s$。

本文由以下两部分组成。第一部分对分数布朗运动的基本知识进行回顾，第二部分给出 $U_t$ 和 $A_t$ 的离散化形式，第三部分我们将给出 $A_t$ 离散化后 $A_{nt}$ 的特征函数。

2. 预备知识

分数布朗运动

定义2.1 分数布朗运动 $B_t^H$ 是定义在完备概率空间 $\left(\Omega ,F,P\right)$ 上具有Hurst指数 $H\in \left(\text{0},1\right)$ 的样本轨道连续的中心高斯过程，且协方差函数满足：

$R_H\left(t,s\right):=E\left(B_t^H{B}_s^H\right)=\frac{1}{2}\left(t^{2H}+s^{2H}-{\left|t-s\right|}^{2H}\right)$ (1)

定义2.2 若 $B_t$ 为标准布朗运动，可定义随机过程：

$B_t^H={\displaystyle {\int }_0^{t}z\left(t,s\right)\text{d}{B}_s,t\in R_{+}}$

其中积分核

$z\left(t,s\right)=C_H\left[{\left(\frac{t}{s}\right)}^{H-\frac{1}{2}}{\left(t-s\right)}^{H-\frac{1}{2}}-\left(H-\frac{1}{2}\right)s^{\frac{1}{2}-H}{\displaystyle {\int }_s^t{u}^{H-\frac{3}{2}}}{\left(u-s\right)}^{H-\frac{1}{2}}\text{d}u\right],H\in \left(0,1\right)$

其中 $C_H={\left(\frac{2H\Gamma \left(\frac{3}{2}-H\right)}{\Gamma \left(H+\frac{1}{2}\right)\Gamma \left(2-2H\right)}\right)}^{\frac{1}{2}}$。

当 $H\in \left(\frac{\text{1}}{\text{2}},1\right)$ 时， $z\left(t,s\right)=C_H\left(H-\frac{1}{2}\right)s^{H-\frac{1}{2}}{\displaystyle {\int }_s^t{u}^{H-\frac{1}{2}}{\left(u-s\right)}^{H-\frac{3}{2}}}\text{d}u$。

定义2.3 若 $B_t^H$ 为Hurst指数 $H\in \left(\frac{1}{2},1\right)$ 的分数布朗运动则定义过程 [8]：

$\begin{array}{l}{B}_{nt}^H:={\displaystyle \underset{i=1}{\overset{[nt]}{\sum }}n{\displaystyle {\int }_{\frac{i-1}{n}}^{\frac{i}{n}}z\left(\frac{\left[nt\right]}{n},s\right)\text{d}s\frac{1}{\sqrt{n}}}}{X}_i,E\left(X_i\right)=0,D\left(X_i\right)=1\\ z\left(t,s\right)=C_H\left(H-\frac{1}{2}\right)s^{\frac{1}{2}-H}{\displaystyle {\int }_s^t{u}^{H-\frac{1}{2}}}{\left(u-s\right)}^{H-\frac{3}{2}}\text{d}u\end{array}$ (2)

当 $n\to \infty$ 时， $B_{nt}^H$ 弱收敛至 $B_t^H$。

3. 指数泛函离散化

定义3.1 若定义相互独立随机变量序列 $\left\{X_i\right\}$ 满足 $E\left(X_i\right)=\frac{-\mu }{\sqrt{n}},D\left(X_i\right)={\sigma }^2$，定义 ${\xi }_{nt}$ 满足： ${\xi }_{nt}:={\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}\sqrt{n}}{\displaystyle {\int }_{\frac{i-1}{n}}^{\frac{i}{n}}z\left(\frac{\left[nt\right]}{n},s\right)\text{d}s{X}_i}$，则有 ${\xi }_{nt}$ 弱收敛至。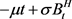

证明：我们将此证明分为两部分。第一部分，我们首先考虑 ${\xi }_{nt}$ 有限维分布的收敛性。对任意 $a_1,a_2,\cdots ,a_d\in R,t_1,t_2,\cdots ,t_d\in \left[0,T\right]$。定义 $Z_n$ 为：

$Z_n:={\displaystyle \underset{k=1}{\overset{d}{\sum }}{a}_k{\xi }_{nt}}$

为证明 $Z_n$ 收敛至方差为 $E{\left({\displaystyle \underset{k=1}{\overset{d}{\sum }}{a}_k{\xi }_{n_{t_k}}}\right)}^2$ 的正态分布，我们首先计算 $Z_n$ 的极限方差。定义 $S_n^2:=D\left(Z_n\right)$。

我们可以得到：

$S_n^2={\displaystyle \underset{k,l=1}{\overset{d}{\sum }}{a}_k{a}_l{\sigma }^{2}n{\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}{\displaystyle {\int }_{\frac{i-1}{n}}^{\frac{i}{n}}z\left(\frac{\left[n_{tk}\right]}{n},s\right)\text{d}s}}}{\displaystyle {\int }_{\frac{i-1}{n}}^{\frac{i}{n}}z\left(\frac{\left[n_{tl}\right]}{n},s\right)\text{d}s}$ (3)

由中值定理得到公式(3)等于

${\displaystyle \underset{k,l=1}{\overset{d}{\sum }}{a}_k{a}_l{\sigma }^2\frac{1}{n}{\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}z\left(\frac{\left[n{t}_k\right]}{n},s_{ni},k\right)z\left(\frac{\left[n{t}_l\right]}{n},s_{ni,l}\right)}}$ (4)

其中 $s_{ni,k},s_{ni,l}\in \left(\frac{i-1}{n},\frac{i}{n}\right]$。因为函数 $z\left(t,\cdot \right)$ 在 $\left(0,T\right]$ 中连续单调递增，从而我们可得公式(3)被积函数等于

$\frac{1}{n}{\sigma }^2{\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}z\left(\frac{\left[n{t}_k\right]}{n},u_{ni}\right)z\left(\frac{\left[n{t}_l\right]}{n},u_{ni}\right)}$ (5)

其中 $u_{ni}\in \left[\min \left(s_{ni,k},s_{ni,l}\right),\max \left(s_{ni,k},s_{ni,l}\right)\right]\subseteq \left(\frac{i-1}{n},\frac{i}{n}\right]$。

从而我们可以得到 $S_n^2$ 是Riemann型积分，核函数z连续，映射 $t\to \frac{\left[nt\right]}{n}$ 一致收敛于 $\left[0,T\right]$ 上的恒等映

射，从而我们可以得到 $S_n^2$ 收敛于：

${\displaystyle \underset{k,l}{\overset{d}{\sum }}{a}_k{a}_l}{\sigma }^2{{\displaystyle {\int }_0^{T}z\left(t_k,s\right)z\left(t_l,s\right)\text{d}s=E\left(\sigma {\displaystyle \underset{k=1}{\overset{d}{\sum }}{a}_k{\xi }_{n{t}_k}}\right)}}^2$ (6)

接下来可以将 $Z_n$ 写作关于i的和：

$Z_n={\displaystyle \underset{k=1}{\overset{d}{\sum }}{a}_k\xi n{t}_k={\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}\sqrt{n}{X}_i}}{\displaystyle \underset{k=1}{\overset{d}{\sum }}ak{\displaystyle {\int }_{\frac{i-1}{n}}^{\frac{i}{n}}z\left(\frac{\left[n{t}_k\right]}{n},s\right)\text{d}s}}={\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}{Z}_{ni}}$ (7)

若 $Z_n$ 满足Lindeberg条件 [9]，我们可以得到对任意 $\epsilon >0$，

$\underset{n\to \infty }{\lim }\frac{1}{S_n^2}{\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}E{\left|Z_{ni}-E{Z}_{ni}\right|}^2{1}_{\left\{\left|Z_{ni}-E{Z}_{ni}\right|>\epsilon S_n\right\}}}=0$

我们将给出 ${\left|Z_{ni}-E{Z}_{ni}\right|}^2$ 的上界。由Cauchy-Schwartz不等式以及 $z\left(\cdot ,s\right)$ 单调递增， $z\left(t,\cdot \right)$ 单调递减。我们可以得到：

$E{Z}_{ni}=E\left[\sqrt{n}{X}_i{\displaystyle \underset{k=1}{\overset{d}{\sum }}{a}_k{\displaystyle {\int }_{\frac{i-1}{n}}^{\frac{i}{n}}z\left(\frac{\left[n{t}_k\right]}{n},s\right)\text{d}s}}\right]=-\mu {\displaystyle \underset{k=1}{\overset{d}{\sum }}{a}_k}{\displaystyle {\int }_{\frac{i-1}{n}}^{\frac{i}{n}}z\left(\frac{\left[n{t}_k\right]}{n},s\right)\text{d}s}$ (8)

$\begin{array}{c}{\left|Z_{ni}-E{Z}_{ni}\right|}^2={\left|\sqrt{n}{X}_i{\displaystyle \underset{k=1}{\overset{d}{\sum }}{a}_k}{\displaystyle {\int }_{\frac{i-1}{n}}^{\frac{i}{n}}z\left(\frac{\left[n{t}_k\right]}{n},s\right)\text{d}s+\mu {\displaystyle \underset{k=1}{\overset{d}{\sum }}{a}_k{\displaystyle {\int }_{\frac{i-1}{n}}^{\frac{i}{n}}z\left(\frac{\left[n{t}_k\right]}{n},s\right)}}}\right|}^2\\ \le n{\left(X_i+\frac{\mu }{\sqrt{n}}\right)}^{2}A{\left({\displaystyle {\int }_{\frac{i-1}{n}}^{\frac{i}{n}}z\left(T,s\right)\text{d}s}\right)}^2\\ \le {\left(X_i+\frac{\mu }{\sqrt{n}}\right)}^{2}A\left({\displaystyle {\int }_{\frac{i-1}{n}}^{\frac{i}{n}}{z}^2\left(T,s\right)\text{d}s}\right)\\ \le {\left(X_i+\frac{\mu }{\sqrt{n}}\right)}^{2}A\left({\displaystyle {\int }_{０}^{\frac{１}{n}}{z}^2\left(T,s\right)\text{d}s}\right)\\ ={\left(X_i+\frac{\mu }{\sqrt{n}}\right)}^{2}A{\delta }_n\end{array}$ (9)

其中 $A:=d{\displaystyle \underset{k=1}{\overset{d}{\sum }}{a}_k^2},{\delta }_n:={\displaystyle {\int }_0^{\frac{1}{n}}{z}^2\left(T,s\right)\text{d}s}$。我们可以得到：

$\left\{\left|Z_{ni}-E{Z}_{ni}\right|>\epsilon S_n\right\}\subseteq \left\{{\left(X_i+\frac{\mu }{\sqrt{n}}\right)}^{2}A{\delta }_n>{\epsilon }^2{S}_n^2\right\}$ (10)

从公式(8)和公式(9)，我们可以得到：

$\begin{array}{l}E{\left|Z_{ni}-E{Z}_{ni}\right|}_1^2{}_{\left\{\left|Z_{ni}-E{Z}_{ni}\right|>\epsilon S_n\right\}}\le E{\left|Z_{ni}-E{Z}_{ni}\right|}_1^2{}_{\left\{{\left(X_i+\frac{\mu }{\sqrt{n}}\right)}^{2}A{\delta }_n>{\epsilon }^2{S}_n^2\right\}}\\ \le E{\left(X_i+\frac{\mu }{\sqrt{n}}\right)}^{2}A{\delta }_{n1}{}_{\left\{{\left(X_i+\frac{\mu }{\sqrt{n}}\right)}^{2}A{\delta }_n>{\epsilon }^2{S}_n^2\right\}}\end{array}$ (11)

从而我们可以得到 ${\left|Z_{ni}-E{Z}_{ni}\right|}^2$ 的上界，进而将其带入Lindeberg条件。

$\begin{array}{l}\frac{1}{S_n^2}{\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}E{\left|Z_{ni}-E{Z}_{ni}\right|}_1^2{}_{\left\{\left|Z_{ni}-E{Z}_{ni}\right|>\epsilon S_n\right\}}}\le \frac{1}{S_n^2}{\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}E{\left(X_i+\frac{\mu }{\sqrt{n}}\right)}^2}A{\delta }_{n1}{}_{\left\{{\left(X_i+\frac{\mu }{\sqrt{n}}\right)}^{2}A{\delta }_n>{\epsilon }^2{S}_n^2\right\}}\\ \le E{\left(X+\frac{\mu }{\sqrt{n}}\right)}_1^2{}_{\left\{{\left(X_i+\frac{\mu }{\sqrt{n}}\right)}^{2}A{\delta }_n>{\epsilon }^2{S}_n^2\right\}}\end{array}$ (12)

其中 $X=X_1$。我们可以得到 $Z_n$ 满足Lindeberg条件， $z{\left(T,\cdot \right)}^2$ 可积公式(12)右侧趋向于0。因此我们可以得到 ${\xi }_{nt}$ 有限维分布的收敛性。

第二部分， 我们将证明 ${\xi }_{nt}$ 的紧性。对任意 $s<t$，由Cauchy-Schwartz不等式，我们可以得到：

$\begin{array}{c}E{\left|{\xi }_{nt}-{\xi }_{ns}\right|}^2=E{\left(\left({\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}\sqrt{n}}{\displaystyle {\int }_{\frac{i-1}{n}}^{\frac{i}{n}}z\left(\frac{\left[nt\right]}{n},u\right)-z}\left(\frac{\left[ns\right]}{n},u\right)\text{d}u\right)X_i\right)}^2\\ \le {\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}E{\left(X_i\right)}^2}{\left(\sqrt{n}{\displaystyle {\int }_{\frac{i-1}{n}}^{\frac{i}{n}}z\left(\frac{\left[nt\right]}{n},u\right)-z}\left(\frac{\left[ns\right]}{n},u\right)\text{d}u\right)}^2\\ ={\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}\left({\sigma }^2+\frac{\mu }{n}\right)}{\displaystyle {\int }_{\frac{i-1}{n}}^{\frac{i}{n}}{\left(z\left(\frac{\left[nt\right]}{n},u\right)-z\left(\frac{\left[ns\right]}{n},u\right)\right)}^2\text{d}u}\\ =\left({\sigma }^2+\frac{\mu }{n}\right){\left|\frac{\left[nt\right]}{n}-\frac{\left[ns\right]}{n}\right|}^{2H}\end{array}$ (13)

接下来对任意 $s\le t\le u$，再次由Cauchy-Schwartz不等式和公式(13)的上界，我们可以得到：

$\begin{array}{l}E\left|{\xi }_{nt}-{\xi }_{ns}\right|\left|{\varsigma }_{nu}-{\xi }_{nt}\right|\le {\left(E{\left({\xi }_{nt}-{\xi }_{ns}\right)}^2\right)}^{\frac{1}{2}}{\left(E{\left({\xi }_{nu}-{\xi }_{nt}\right)}^2\right)}^{\frac{1}{2}}\\ \le \left({\sigma }^2+\frac{\mu }{n}\right){\left|\frac{\left[nt\right]}{n}-\frac{\left[ns\right]}{n}\right|}^H{\left|\frac{\left[nu\right]}{n}-\frac{\left[nt\right]}{n}\right|}^H\\ \le \left({\sigma }^2+\frac{\mu }{n}\right){\left|\frac{\left[nu\right]}{n}-\frac{\left[ns\right]}{n}\right|}^{2H}\end{array}$ (14)

我们可以得到公式(14)的收敛性：

1. 若 $u-s\ge \frac{1}{n}$，则有 $E\left|{\xi }_{nt}-{\xi }_{ns}\right|\left|{\xi }_{nu}-{\xi }_{nt}\right|\le \left({\sigma }^2+\frac{\mu }{n}\right){\left|2\left(u-s\right)\right|}^{2H}$

2. 若 $u-s<\frac{1}{n}$，我们可以得到对任意m，s和t或者t和u在同一区间 $\left[\frac{m}{n},\frac{m+1}{n}\right)$，从而可以得到公式的左边为0。由此对任意 $s<t<u$，上式仍成立。当 $H>\frac{1}{2}$，我们可以得到 ${\xi }_{nt}$ 的紧性。

引理3.2 为简便计算，我们可以得到核函数 $z\left(\frac{\left[nt\right]}{n},s\right)$ 的上下界，由 $z\left(\cdot ,s\right)$ 单调递增和 $z\left(t,\cdot \right)$ 单调递减，我们可以得到：

$0\le z\left(\frac{\left[nt\right]}{n},\frac{i}{n}\right)\le z\left(\frac{\left[nt\right]}{n},s\right)\le z\left(\frac{\left[nt\right]}{n},\frac{i-1}{n}\right)$ (15)

$z\left(\cdot ,s\right)$ 连续。由中值定理，我们可以假设存在一系列由t，i决定的正整数 $C_i$ 满足：

${\displaystyle {\int }_{\frac{i-1}{n}}^{\frac{i}{n}}z\left(\frac{\left[nt\right]}{n},s\right)\text{d}s=\frac{C_i}{n}}$ (16)

从而我们可以记作： ${\xi }_{nt}:={\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}{\xi }_{ni}}$，其中 ${\xi }_{ni}=\frac{C_i}{\sqrt{n}}{X}_i$。

定理3.3 定义过程 $V_{nt}:={\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\prod }}\left(1+{\xi }_{ni}\right)}$， $V_{nt}$ 收敛至 $U_t={\text{e}}^{\sigma B_t^H-\mu t}$。

证明：由泰勒公式 $\log \left(1+x\right)=x-\frac{1}{2}{x}^2+r\left(x^2\right)$，当x趋于0时， $r\left(x^2\right)$ 趋于0，可得，

$\log V_{nt}={\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}\log \left(1+{\xi }_{ni}\right)}={\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}\left({\xi }_{ni}-\frac{1}{2}{\left({\xi }_{ni}\right)}^2+r\left({\xi }_{ni}^2\right)\right)}={\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}{\xi }_{ni}-\frac{1}{2}}{\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}{\left({\xi }_{ni}\right)}^2+}{\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}r\left({\xi }_{ni}^2\right)}$ (17)

接下来证明 ${\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}{\xi }_{ni}^2}$ 和 ${\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}r\left({\xi }_{ni}^2\right)}$ 趋于0。

$E\left({\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}{\xi }_{ni}^2}\right)=E\left({\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}{\left(\frac{C_i}{\sqrt{n}}{X}_i\right)}^2}\right)={\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}E{X}_i^2\frac{C_i^2}{n}}$ (18)

由Markov不等式，对任意n，当 $n\to \infty$，

$P\left(\left|{\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}{\xi }_{ni}^2-0}\right|>\frac{1}{n}\right)\le \frac{E\left({\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}{\xi }_{ni}^2}\right)}{\frac{1}{n}}={\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}\left({\sigma }^2+\frac{{\mu }^2}{n}\right)C_i^2}$ (19)

当 $\mu <\frac{1}{\sqrt{n}},{\sigma }^2<\frac{1}{n^2}$，当 $n\to \infty$，我们可以得到公式(19)趋于0，从而我们可以得到 ${\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}{\xi }_{ni}^2}$ 和 ${\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}r\left({\xi }_{ni}^2\right)}$ 依概率收敛于0。

我们可以得到当 $n\to \infty$， $\log V_{nt}$ 收敛至 ${\displaystyle \underset{i=1}{\overset{\left[nt\right]}{\sum }}{\xi }_n{}_i}$， $V_{nt}$ 收敛至 ${\text{e}}^{\sigma B_t^H-\mu t}$。

定理3.4 定义过程 $V_{n{t}_j}={\displaystyle \underset{i=1}{\overset{\left[n{t}_j\right]}{\sum }}{Y}_{ni}}$，其中 $Y_{ni}=\left(1+{\xi }_{ni}\right),t_j=\frac{j}{n},j=1,2,\cdots ,\left[nt\right]$。定义过程 $A_{nt}=n^{-1}{\displaystyle \underset{j=1}{\overset{\left[nt\right]}{\sum }}{V}_{n{t}_j}}$， $A_{nt}$ 收敛至 ${\displaystyle {\int }_0^t{\text{e}}^{\sigma B_s^H-\mu s}}\text{d}s$。

证明：我们将此证明分为两部分。第一部分，我们将 ${\displaystyle {\int }_0^t{\text{e}}^{\sigma B_s^H-\mu s}}\text{d}s$ 写作Riemann和形式。定义 $g\left(s_j\right)={\text{e}}^{\sigma B_{s_j}^H-\mu s_j}$，其中 $s_j=\frac{j}{n},j=1,2,\cdots ,\left[nt\right]$。从而我们可以得到，对任意n，存在 $N>0$，当 $n>N$ 时，我们有：

$\left|n^{-1}{\displaystyle \underset{j=1}{\overset{\left[nt\right]}{\sum }}g\left(s_j\right)-{\displaystyle {\int }_0^t{\text{e}}^{\sigma B_s^H-\mu s}}}\text{d}s\right|<\frac{1}{n}$ (20)

由定理3.3可知，存在一系列 $N_j>0$，当 $n>\max \left\{N_j\right\}$ 时，我们有：

$\left|V_{n{t}_j}-{\text{e}}^{\sigma B_{t_j}^H-\mu t_j}\right|<\frac{1}{n}$

第二部分，当 $n>\max \left\{N,\max \left\{N_j\right\}\right\}$，由公式(20)，我们可以得到：

$\begin{array}{c}\left|A_{nt}-{\displaystyle {\int }_0^t{\text{e}}^{\sigma B_s^H-\mu s}\text{d}s}\right|\\ =\left|n^{-1}{\displaystyle \underset{j=1}{\overset{\left[nt\right]}{\sum }}{V}_{n{t}_j}-n^{-1}{\displaystyle \underset{j=1}{\overset{\left[nt\right]}{\sum }}g\left(s_j\right)+n^{-1}{\displaystyle \underset{j=1}{\overset{\left[nt\right]}{\sum }}g\left(s_j\right)}-{\displaystyle {\int }_0^t{\text{e}}^{\sigma B_s^H-\mu s}\text{d}s}}}\right|\\ \le \frac{\left|V_{n{t}_1}-g\left(s_1\right)+\cdots +V_{n{t}_{\left[nt\right]}}-g\left(s_{\left[nt\right]}\right)\right|}{n}+\left|n^{-1}{\displaystyle \underset{j=1}{\overset{\left[nt\right]}{\sum }}g\left(s_j\right)-{\displaystyle {\int }_0^t{\text{e}}^{\sigma B_s^H-\mu s}\text{d}s}}\right|\\ \le \frac{1}{n}+\frac{\left[nt\right]}{n^2}\end{array}$ (21)

从而当 $n\to \infty$ 时， $A_{nt}$ 收敛至 ${\displaystyle {\int }_{\text{0}}^t{\text{e}}^{\sigma B_s^H-\mu s}}\text{d}s$。

4. A_t与A_nt的分布

定理4.1 若 $\mu >0$，当 $t\to \infty$ 时， $A_t={\displaystyle {\int }_{\text{0}}^t{\text{e}}^{\sigma B_s^H-\mu s}}\text{d}s$ 几乎处处收敛。

证明：由分数布朗运动的重对数律 [10] 可得：

$\underset{s\to \infty }{\lim }\frac{B_s^H}{s^H\sqrt{\log \log s}}=C_H$ (22)

其中 $C_H$ 为常数，从而我们可以得到：

$\underset{s\to \infty }{\lim }\frac{\sigma B_s^H}{s}=\underset{s\to \infty }{\lim }\sigma \cdot \frac{B_s^H}{s^H\sqrt{\log \log s}}\cdot \frac{s^H\sqrt{\log \log s}}{s}=0$ (23)

公式表明存在 $0\le \epsilon \le \mu$ 和 $S\left(\epsilon \right)$，当 $s>S(\; \epsilon \; )$

${\text{e}}^{\frac{\sigma B_s^H-\mu s}{s}}={\text{e}}^{\frac{\sigma B_s^H}{s}-\mu }\le {\text{e}}^{\epsilon -\mu }$ (24)

从而可以得到，当 $t\to \infty$ 时， $A_t$ 几乎处处收敛。

为了考虑 $A_{nt}=n^{-1}{\displaystyle \underset{j=1}{\overset{\left[nt\right]}{\sum }}{V}_{n{t}_j}}$ 的分布，我们需要计算 $X_i,{\xi }_{ni}$ 和 $Y_n{}_i$ 的一阶矩和二阶矩：

$E\left(X_i\right)=\frac{-\mu }{\sqrt{n}},D\left(X_i\right)={\sigma }^2,E\left(X_i^2\right)=D\left(X_i\right)+E{\left(X_i\right)}^2={\sigma }^2+\frac{{\mu }^2}{n}$

$\begin{array}{l}{\xi }_{ni}=\frac{C_i}{\sqrt{n}}{X}_i,E\left({\xi }_{ni}\right)=\frac{-\mu C_i}{n},\\ D\left({\xi }_{ni}\right)=E{\left({\xi }_{ni}-E\left({\xi }_{ni}\right)\right)}^2=E{\left(\frac{C_i}{\sqrt{n}}{X}_i+\frac{\mu C_i}{n}\right)}^2=\frac{{\sigma }^2{C}_i^{\text{2}}}{n}\end{array}$ (25)

$Y_{ni}=1+{\xi }_{ni}$，我们可以得到：

$\begin{array}{l}E\left(Y_{ni}\right)=E\left(1+{\xi }_{ni}\right)=1-\frac{\mu C_i}{n},D\left(Y_{ni}\right)=E{\left(Y_{ni}-E\left(Y_{ni}\right)\right)}^2=\frac{{\sigma }^2{C}_i^2}{n},\\ E\left(Y_{ni}^2\right)=D\left(Y_{ni}\right)+{\left(E\left(Y_{ni}\right)\right)}^2=1+\frac{{\sigma }^2{C}_i^2-2\mu C_i}{n}+\frac{{\mu }^2{C}_i^2}{n^2}\end{array}$

接下来我们将计算 $V_{nt}$ 与 $A_{nt}$ 的特征函数。

定理4.2 定义为随机变量的特征函数，从而我们可以得到以下公式：

${\phi }_{\theta }\left(x\right)=E\left({\text{e}}^{jx\theta }\right),{\phi }_{\theta }^{\left(k\right)}\left(0\right)=j^{k}E\left({\theta }^k\right),j^2=-1$

${\phi }_{\theta }\left(x\right)={\phi }_{\theta }\left(0\right)+{\phi }_{\theta }^{\left(1\right)}\left(0\right)x+\frac{1}{2}{\phi }_{\theta }^{\left(2\right)}\left(0\right)x^2+o\left(x^2\right)$ (26)

由定理4.1知， $A_{nt}=n^{-1}{\displaystyle \underset{j=1}{\overset{\left[nt\right]}{\sum }}{V}_{n{t}_j}}$，记 $A_{n{t}_j}=\frac{V_{n{t}_j}}{n}$ 为相互独立同分布随机变量，从而我们可以得到：

$\phi A_{nt}\left(x\right)={\phi }_{{\displaystyle \underset{j=1}{\overset{\left[nt\right]}{\sum }}An{t}_j}}\left(x\right)={\displaystyle \underset{j=1}{\overset{\left[nt\right]}{\prod }}\phi A_{ntj}}\left(x\right)$ (27)

首先我们计算 ${\phi }_{An{t}_j}\left(x\right)$，

$\begin{array}{l}E\left(A_{n{t}_j}\right)=E\left(\frac{V_{n{t}_j}}{n}\right)=E\left(\frac{{\displaystyle \underset{i=1}{\overset{\left[n{t}_j\right]}{\prod }}{Y}_{ni}}}{n}\right)=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{\left[n{t}_j\right]}{\prod }}\left(1-\frac{\mu C_i}{n}\right)}\\ E\left(A_{n{t}_j}^2\right)=E\left(\frac{V_{n{t}_j}^2}{n^2}\right)=\frac{1}{n^2}{\displaystyle \underset{i=1}{\overset{\left[n{t}_j\right]}{\prod }}E\left(Y_{ni}^2\right)}=\frac{1}{n^2}{\displaystyle \underset{i=1}{\overset{\left[n{t}_j\right]}{\prod }}\left(1+\frac{C_i^2{\sigma }^2-2\mu C_i}{n}+\frac{{\mu }^2{C}_i^2}{n^2}\right)}\end{array}$ (28)

我们记 $E\left(A_{n{t}_j}\right)=G\left(n,\left[n{t}_j\right]\right),E\left(A_{n{t}_j}^2\right)=H\left(n,\left[n{t}_j\right]\right)$。我们将公式(28)代入公式(26)，我们可以得到：

${\phi }_{An{t}_j}\left(x\right)=1+jG\left(n,\left[n{t}_j\right]\right)x-\frac{1}{2}H\left(n,\left[n{t}_j\right]\right)x^2+O\left(x^2\right)$ (29)

由公式，我们可以得到：

${\phi }_{A_{nt}}\left(x\right)={\phi }_{{\displaystyle \underset{j=1}{\overset{\left[nt\right]}{\sum }}An{t}_j}}\left(x\right)={\displaystyle \underset{j=1}{\overset{\left[nt\right]}{\prod }}\left(1+jG\left(n,\left[n{t}_j\right]\right)x-\frac{1}{2}H\left(n,\left[n{t}_j\right]\right)x^2+O\left(x^2\right)\right)}$ (30)

进而我们可以得到：

${\phi }_{A_t}\left(x\right)=\underset{n\to \infty }{\lim }{\phi }_{Ant}(\; x\; )$