东濮老油田注水井分层启动压力预测技术研究

Study on Stratified Starting Pressure Prediction Technology for Injection Wells in Dongpu Mature Oilfield

摘要: 分层启动压力是确定分层注水方案的主要依据，是开展多层油藏层间治理，实现精细注水的前提和基础。本文基于中原油田东濮老区油藏特性，研究了启动压力梯度随储层物性的变化规律，基于BP神经网络建立了小层启动压力预测模型，形成一套适合油藏特点的启动压力求取方法，对于指导油田精细注水、改善注水开发效果具有重要意义。

Abstract: The stratified starting pressure is the main basis to determine the stratified water injection program. Based on the reservoir characteristics of Dongpu mature area of Zhongyuan oilfield, this paper studies the variation rule of starting pressure gradient with reservoir physical property. A small layer startup pressure prediction model based on BP neural network is established. A set of starting pressure calculation method suitable for reservoir characteristics is formed. The method is of great significance for guiding fine water injection and improving the effect of water injection development.

1. 前言

中原油田属于多层砂岩复杂断块油藏，层内非均质性强，层间渗透率级差大，经过长期注水开发，层间矛盾进一步加剧。注水井各小层吸水不均匀，导致纵向上注水波及体积小，水驱效率低。渗透率较高层吸水很多，产生单层突进现象，而低渗层却不吸水 [1]。确定小层启动压力是老油田开展多层油藏层间治理、实现精细注水的前提和基础。

目前国内外有关油藏注水启动压力方面的研究极少，荣准 [2] 等人在考虑储层物性参数和油藏动态因素的基础上，基于有限的现场分层测试资料，采用神经网络方法预测注水启动压力。但由于考虑的因素不全，未考虑启动压力梯度影响，且采用的样本数据有限，因此研究成果不具备普遍推广应用价值。

常规确定注水井小层启动压力的测试方法有管柱法、氧活化测试 [3]、试井解释及分层测试等。受储层条件及井况的限制，分层启动压力测试技术难度大，成本高，测试周期长，同时由于分层启动压力测试井数少而且分散，难以形成规律性认识。

本文通过开展岩心高压驱替试验，确定注水启动压力的主要影响因素，研究启动压力梯度随储层物性的变化规律，建立小层启动压力预测模型，形成一套适合油藏特点的启动压力求取方法，对于指导油田精细注水、改善注水开发效果、提高注水效率和经济效益等，具有重要意义。

2. 启动压力梯度实验研究

采用稳态法岩心驱替试验，从物性、压力、不同渗透率组合等方面开展启动压力梯度与岩石主要物性参数之间的关系研究 [4]，确定启动压力梯度的主要影响因素。

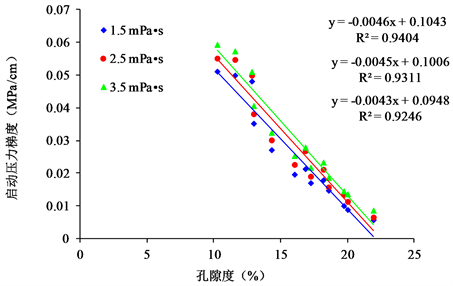
Figure 1. Chart of relationship between starting pressure gradient and porosity

图1. 启动压力梯度与孔隙度关系图版

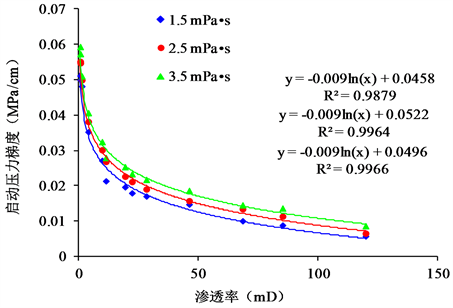
Figure 2. Chart of relationship between starting pressure gradient and permeability

图2. 启动压力梯度与渗透率关系图版

从图1、图2中可以看出随着岩心孔隙度、渗透率的降低，启动压力梯度分别呈上升趋势，其中渗透率小于10 × 10⁻³ μm²时，启动压力梯度随渗透率的减小急剧增大，注水难度增大。

通过实验分析，影响启动压力梯度的主要因素包括：孔隙度、渗透率、束缚水饱和度、残余油饱和度、含水饱和度、平均孔喉半径(粒度中值)、原油粘度等，其中某些因素的影响是显著的，某些是不敏感的。选择束缚水饱和度、黏土含量、孔隙度、渗透率、粒度中值、残余油饱和度、原油粘度、平均孔吼半径，等参数作为预考虑的影响参数。通过灰色关联分析，用灰色关联度的大小来描述因素之间联系的强弱与顺序关系。

3. 注水小层启动压力影响因素研究

以渗流力学理论为依据 [5]，采用灰色关联分析法 [6]，选择孔隙度、渗透率、油水粘度比、黏土含量、束缚水饱和度、含水饱和度、残余油饱和度、启动压力梯度、地层压力、吸水指数、吸水层有效厚度、表皮系数12个参数作为注水分层启动压力的预考虑影响因素。

根据关联度计算结果排序为地层压力 > 渗透率 > 残余油饱和度 > 含水饱和度 > 束缚水饱和度 > 启动压力梯度 > 油水粘度比 > 孔隙度 > 吸水指数 > 黏土含量 > 吸水层有效厚度 > 表皮系数。

研究表明，目的区块地层压力、渗透率、残余油饱和度、含水饱和度、束缚水饱和度、启动压力梯度、油水粘度比、孔隙度、吸水指数对分层启动压力影响显著，黏土含量、吸水层有效厚度、表皮系数对分层启动压力影响相对较弱。

4. 注水小层启动压力预测方法研究

由于启动压力是一个多因素影响下的非线性因素，利用人工神经网络原理建立启动压力的BP人工神经网络预测模型。

4.1. BP神经网络

BP神经网络是一种按误差反向传播(误差反传)训练的多层前馈网络 [7] (见图3)。BP算法包括信号的正向传播和误差的反向传播 [8] 两个过程，即计算误差输出时按从输入到输出的方向进行，而调整权值和阈值则从输出到输入的方向进行。输入层各神经元接收来自外界的输入信息，并传递给中间层各神经元，而中间层负责信息转换，误差通过输出层，按误差梯度下降的方式修正各单元权值，向隐层、输入层逐层反传 [9]。经过反复学习训练，神经网络即能对类似样本的输入信息自行处理输出误差最小的经过非线形转换的信息(见图4)。

Figure 3. Structure of BP network

图3. BP网络结构

Figure 4. Three layer BP network diagram

图4. 三层BP网络图

输出层的输出向量用o表示，其中列向量 $o_k$ 为输出层第k个神经元对应的输出向量；期望输出向量用d表示，其中列向量 $d_k$ 为输出层第k个神经元对应的期望输出向量；输入层到隐含层之间的权值矩阵用v表示，其中列向量 $v_{ij}$ 为由输入层第i个神经元输入隐含层，在隐含层中第j个神经元对应的权向量；隐含到输出层之间的权值矩阵用w 表示 ，其中列向量 $w_{jk}$ 为由隐含层第j个神经元输入输出层，在输出层中第k个神经元对应的权向量；i表示输入神经元个数；j表示隐含层神经元个数；k表示输出神经元个数。

对于一个单隐层的三层感知器，各层信号之间的数学关系 [10] 如下：

对于输出层：

$o_k=f\left(ne{t}_k\right),k=1,2,\cdots ,l$ (1)

$ne{t}_k={\displaystyle \underset{j=0}{\overset{m}{\sum }}{w}_{jk}{y}_j},k=1,2,\cdots ,l$ (2)

对于隐含层：

$y_j=f\left(ne{t}_j\right),j=1,2,\cdots ,m$ (3)

$ne{t}_j={\displaystyle \underset{i=0}{\overset{n}{\sum }}{v}_{ij}{x}_i},j=1,2,\cdots ,m$ (4)

变换函数 $f\left(x\right)$ 均为单极性Sigmoid函数

$f\left(x\right)=\frac{1}{1+{\text{e}}^{-x}}$ (5)

当网络输出与期望输出不等时，存在输出误差E，定义如下

$E=\frac{1}{2}{\left(d-O\right)}^2=\frac{1}{2}{\displaystyle \underset{k=1}{\overset{l}{\sum }}{\left(d_k-o_k\right)}^2}$ (6)

对于隐层有

$E=\frac{1}{2}{\displaystyle \underset{k=1}{\overset{l}{\sum }}{\left[d_k-f\left(ne{t}_k\right)\right]}^2}=\frac{1}{2}{{\displaystyle \underset{k=1}{\overset{l}{\sum }}\left[d_k-f\left({\displaystyle \underset{j=0}{\overset{m}{\sum }}{w}_{jk}{y}_j}\right)\right]}}^2$ (7)

对于输入层有

$E=\frac{1}{2}{{\displaystyle \underset{k=1}{\overset{l}{\sum }}\left\{d_k-f\left[{\displaystyle \underset{j=0}{\overset{m}{\sum }}{w}_{jk}f\left(ne{t}_j\right)}\right]\right\}}}^2=\frac{1}{2}{{\displaystyle \underset{k=1}{\overset{l}{\sum }}\left\{d_k-f\left[{\displaystyle \underset{j=0}{\overset{m}{\sum }}{w}_{jk}f\left({\displaystyle \underset{i=0}{\overset{n}{\sum }}{v}_{ij}{x}_i}\right)}\right]\right\}}}^2$ (8)

网络输入误差是各层权值 $w_{jk}$ 、 $v_{ij}$ 的函数，调整仅值可改变误差E。调整权值的原则是使误差不断地减少，因此应使用权值的调整量与误差的梯度下降成正比，即：

$\Delta w_{jk}=-\eta \frac{\partial E}{\partial w_{jk}},j=0,1,2,\cdots ,m;k=1,2,\cdots ,l$ (9)

$\Delta v_{ij}=-\eta \frac{\partial E}{\partial v_{ij}},j=0,1,2,\cdots ,n;k=1,2,\cdots ,m$ (10)

式中，负号表示梯度下降，常数 $\eta \in \left(0,1\right)$ 表示比例系数， $\eta$ 为学习速率，y为本层输入信号， $\delta$ 为本层输出的误差信号。

4.2. 分层启动压力预测

基于上述BP神经网络理论方法和灰色关联分析结果，确定小层启动压力的主要影响因素，剔除无关和不敏感因素，以束缚水饱和度、地层压力、黏土含量、残余油饱和度、粒度中值、原油粘度、含水饱和度、启动压力梯度、绝对吸水量、孔隙度、吸水层有效厚度、吸水指数、渗透率等参数作为参与训练学习的影响因素参数，启动压力作为目标函数。BP神经网络通过训练学习，多次检验误差来调试模型误差达到最小，最终确定误差最小且较为合理的模型参数，建立稳定的预测模型，利用这个预测模型即可预测在诸多影响因素为已知情况下的启动压力。

收集整理W81和PNS2X两个区块的物性数据及分层启动压力测试资料作为样本数据，进行训练学习。随着样本数据训练次数的增加，各层预测误差进一步减小，拟合程度较好，网络训练后的预测值与实际值误差有较大的改善(见图5)，检测结果证明网络稳定，收敛速度快，预测的结果可信(见表1)。

Figure 5. Variation of network error with training times

图5. 网络误差随训练次数的变化图

Table 1. Network training parameters and overall relative error

表1. 网络训练参数与总体相对误差

根据建立的区块启动压力预测模型，分别对部分注水井小层启动压力进行了预测分析，表2列出了实验数据与预测结果，可以看出，根据启动压力预测模型计算的预测结果与实测数据符合性较好，相对误差基本控制在一定范围内，预测结果是准确的。

Table 2. Experimental data and prediction results

表2. 实验数据与预测结果

5. 结论

1) 结果表明：基于BP神经网络，建立综合考虑启动压力梯度、储层特性及注水条件等因素的注水小层启动压力预测技术是可行和可靠的，适用于同类油藏在没有测试资料的条件下确定各小层启动压力，可以为分层治理提供决策依据，有效指导老区精细注采，提高水驱动用程度。

2) 应用区块样本数据的准确性对于启动压力预测数据的精度有着直接的关系，建议结合油藏地质特性建立相关物性参数模型，以保证样本数据的准确性，提高小层启动压力预测的精度。

3) 分层启动压力的影响因素较多，这些因素之间又存在一定的关联，并且不同地区各影响因素之间的关联性不是一成不变的，针对目标油藏的影响因素分析及小层启动压力预测有待进一步研究和完善。