求解双曲守恒律方程的WENO-AO型熵稳定格式

WENO-AO Type Entropy Stable Scheme for Solving Hyperbolic Conservation Law Equations

摘要: 通过在单元交界面处进行WENO-AO重构，构造了一种求解双曲守恒律方程的高分辨率熵稳定格式。该格式有三个优势：1) 该格式在光滑区域是五阶精度的，同时在间断附近无伪振荡产生；2) 在对称条件下，线性权值可以是任意和为1的正数；3) 该格式可以避免极值的裁剪。数值实验表明，该格式具有良好的鲁棒性、高分辨率等特性。

Abstract: By performing WENO-AO reconstruction at the interface of the cells, a high-resolution entropy stable scheme for solving hyperbolic conservation law equations is constructed. This scheme has three advantages: 1) The scheme has fifth-order accuracy in the smooth area, and there is no spurious oscillation near the discontinuity. 2) Under the condition of symmetry, the linear weight can be any positive number with the sum of 1. 3) This scheme can avoid extreme clipping. Numerical experiments show that the scheme has good robustness, high resolution and so on.

1. 引言

双曲守恒律方程广泛应用于科学和工程计算中。如海洋学(浅水方程)、空气动力学(欧拉方程)、等离子体物理学(MHD方程)和结构力学(非线性弹性)。在一维情形下，它们具有如下形式：

$\begin{array}{l}{u}_t+f{\left(u\right)}_x=0\forall \left(x,t\right)\in ℝ\times {ℝ}_{+}\\ u\left(x,0\right)=u_0\left(x\right)\forall x\in ℝ\end{array}$ (1.1)

其中 $u:ℝ\times {ℝ}_{+}\mapsto {ℝ}^m$ 是守恒变量， $f\left(u\right):{ℝ}^m\to {ℝ}^m$ 是相应的通量函数。众所周知，即使所给的初始条件充分光滑，方程(1.1)的解在时间推进的某个时刻也可能会出现间断，产生激波、接触间断等现象。因此，寻求满足方程(1.1)的唯一弱解成为主要挑战。为此引入了熵条件：

$\eta {\left(u\right)}_t+q{\left(u\right)}_x\le 0$ (1.2)

其中： $\left(\eta ,q\right)$ 为熵对，熵函数 $\eta :{ℝ}^m\to ℝ$ 是一个凸函数，熵通量函数 $q:{ℝ}^m\to ℝ$ 满足 ${\partial }_{u}q=v^{\text{T}}{\partial }_{u}f$，并称 $v={\partial }_u\eta$ 为熵变量。从而确定了满足相关物理特性的唯一弱解。

Tadmor等人提出的熵稳定格式一直备受关注。该格式由熵守恒通量和耗散项两部分构成。熵守恒通量在光滑区域表现良好，保持总熵不变。但在激波等间断区域会产生伪振荡，需要添加合适的数值粘性来维持熵的耗散。由于Roe格式对激波有良好的捕捉效果，Ismail和Roe对其数值粘性项加以延拓，并将之添加到熵守恒通量上，得到了熵稳定格式。该格式可有效避免伪振荡等现象，但在空间方向上只能达到一阶精度。科研工作者们构造了一系列高阶熵稳定格式，但其稳定性不佳。

本文基于熵稳定格式，通过在单元交界面处进行高阶WENO-AO型重构，采用三阶强稳定(SSP) Runge Kutta离散化方法进行时间推进，得到了一种求解双曲守恒律方程的高分辨率数值格式。最后，通过一些数值算例验证该格式的性能。

2. 熵稳定格式

考虑R中的Cartesian网格 ${\left\{x_j\right\}}_{j\in Z}$，规定空间离散化单元中心为 $I_j=\left[x_{j-\frac{1}{2}},x_{j+\frac{1}{2}}\right]$，网格大小为 $h=\Delta x=x_{j+1}-x_j$， $x_j$ 为 $I_j$ 的中点值。则半离散守恒格式(1.1)的解为：

$\frac{\text{d}}{\text{d}t}{u}_j\left(t\right)=-\frac{1}{h_j}\left({\hat{f}}_{j+\frac{1}{2}}-{\hat{f}}_{j-\frac{1}{2}}\right)$ (2.1)

这里 $u_j\left(t\right)=u\left(x_j,t\right)$， ${\hat{f}}_{j+\frac{1}{2}}$ 是与 $f$ 相容的数值通量，满足 $\hat{f}\left(u,u,\cdots ,u\right)=f\left(u\right)$。相应地，格式(1.3)称为熵守恒的，如果它满足离散熵准则：

$\frac{\text{d}}{\text{d}t}\eta \left(u_j\left(t\right)\right)+\frac{1}{h_j}\left({\hat{q}}_{j+\frac{1}{2}}-{\hat{q}}_{j-\frac{1}{2}}\right)=0$ (2.2)

这里 ${\hat{q}}_{j+\frac{1}{2}}$ 与熵通量函数相容，即

${\hat{q}}_{j+\frac{1}{2}}=\hat{q}\left(u_{j-p+1},\cdots ,u_{j+p}\right),\hat{q}\left(u,u,\cdots ,u\right)=q\left(u\right)$ (2.3)

定理2.1 (Tadmor [1] )如果 ${\hat{f}}_{j+\frac{1}{2}}$ 对所有的j满足

${\left[v\right]}_{j+\frac{1}{2}}\cdot {\hat{f}}_{j+\frac{1}{2}}={\left[\psi \right]}_{j+\frac{1}{2}}$ (2.4)

那么格式(2.1)是熵守恒的，其数值熵通量为：

$q_{j+\frac{1}{2}}={\bar{v}}_{j+\frac{1}{2}}\cdot {\hat{f}}_{j+\frac{1}{2}}-{\bar{\psi }}_{j+\frac{1}{2}}$ (2.5)

这里 $\psi$ 为熵势， ${[\ast ]}_{j+\frac{1}{2}}:={(\ast )}_{j+1}-{(\ast )}_j,{\left(\bar{\ast }\right)}_{j+\frac{1}{2}}=\frac{{(\ast )}_j\text{+}{(\ast )}_{j+1}}{2}$。

1) 对于标量方程(N = 1)，(2.4)有唯一的二阶精度熵守恒通量：

$f_{j+\frac{1}{2}}^{EC}\left(u_j,u_{j+1}\right)=\{\begin{array}{l}\frac{\psi \left(v_{j+1}\right)-\psi \left(v_{j-1}\right)}{v_{j+1}-v_{j-1}},u_j\ne u_{j+1}\\ f\left(u_j\right),u_j=u_{j+1}\end{array}$， (2.6)

2) 一维理想气体的Euler方程为：

$u_t+f{\left(u\right)}_x=0$， (2.7)

这里 $u={\left(\rho ,\rho u,E\right)}^{\text{T}},f\left(u\right)={\left(\rho u,\rho u^2+p,\rho uH\right)}^{\text{T}}$，变量 $\rho$ 、u、 $p=\left(\gamma -1\right)\left(E-\frac{1}{2}\rho u^2\right)$ 、E、 $H=\left(E+p\right)/\rho$ 分别代表密度、速度、压力、总能和总焓， $\gamma =1.4$ 为理想气体常数。

我们使用热力学熵函数和熵通量函数对来求解欧拉方程：

$\eta \left(u\right)=\frac{-\rho s}{\gamma -1},q\left(u\right)=\frac{-\rho us}{\gamma -1}$， (2.8)

其中物理熵为 $s=\ln p-\gamma \ln \rho$。计算可得，熵变量为

$v=\frac{\partial U}{\partial u}={\left(\frac{\gamma -s}{\gamma -1}-\frac{\rho u^2}{2p},\frac{\rho u}{p},-\frac{\rho }{p}\right)}^{\text{T}}$，熵势为 $\psi \left(v\right)=\rho u$，熵守恒通量满足 $v^{\text{T}}{f}^{EC}=〚\psi 〛$。

在文献 [2] 中，Ismail和Roe构造了Euler方程中 $v^{\text{T}}{f}^{EC}=〚\psi 〛$ 的显式解。定义平均状态：

$z=\left(\begin{array}{l}{z}_1\\ z_2\\ z_3\end{array}\right)=\sqrt{\frac{\rho }{p}}\left(\begin{array}{l}1\\ u\\ p\end{array}\right)$ (2.9)

则单元交界面 $x_{j+\frac{1}{2}}$ 处的熵守恒通量函数为：

$f_{j+\frac{1}{2}}^{EC}{}^{EC}={\left(\begin{array}{l}\hat{\rho }\hat{u}\\ \hat{\rho }{\hat{u}}^2+{\hat{p}}_1\\ \hat{\rho }\hat{u}\hat{H}\end{array}\right)}_{}$ (2.10)

其中 $\hat{u}=\frac{{\bar{z}}_2}{{\bar{z}}_1},\hat{\rho }={\bar{z}}_1{z}_3^{\ln },{\hat{p}}_1=\frac{{\bar{z}}_3}{{\bar{z}}_1},{\hat{p}}_2=\frac{\gamma +1}{2\gamma }\frac{z_3^{\ln }}{z_1^{\ln }}+\frac{\gamma -1}{2\gamma }\frac{{\bar{z}}_3}{{\bar{z}}_1},\hat{a}={\left(\frac{\gamma {\hat{p}}_2}{\hat{\rho }}\right)}^{\frac{1}{2}},\hat{H}=\frac{{\hat{a}}^2}{\gamma -1}+\frac{{\hat{u}}^2}{2}$，对数平均为：

${(\ast )}_{j+\frac{1}{2}}^{\ln }=\frac{{〚\ast 〛}_{j+\frac{1}{2}}}{{〚\ln (\ast )〛}_{j+\frac{1}{2}}}$。

这些熵守恒格式适用于熵保持的光滑流，但在激波处会出现伪振荡。而这些振荡产生的原因是——熵守恒格式无法在激波附近产生足够的所需熵。故需在熵守恒通量中添加适当的耗散算子来抑制伪振荡的产生。

定理2.2 (Tadmor [3] )假设 $D_{j+\frac{1}{2}}\ge 0$， $f_{j+\frac{1}{2}}^{EC}$ 是一个熵守恒通量，若数值通量形式为

${\hat{f}}_{j+\frac{1}{2}}=f_{{}_{j+\frac{1}{2}}}^{EC}-\frac{1}{2}{D}_{j+\frac{1}{2}}{\left[v\right]}_{j+\frac{1}{2}}$ (2.11)

那么格式(2.1)是熵稳定的。即，它满足离散熵不等式

$\frac{\text{d}}{\text{d}t}\eta \left(u_j\left(t\right)\right)+\frac{1}{h_j}\left({\hat{q}}_{j+\frac{1}{2}}-{\hat{q}}_{j-\frac{1}{2}}\right)\le 0$ (2.12)

设 $A=R\Lambda R^{-1}$ 为雅可比矩阵， $\Lambda$ 是相应特征值组成的对角矩阵，R为相应地右特征向量矩阵。则正耗散矩阵可以写为 $D_{i+\frac{1}{2}}=R_{i+\frac{1}{2}}{\stackrel{⌢}{\Lambda }}_{i+\frac{1}{2}}{B}_{i+\frac{1}{2}}{R}_{i+\frac{1}{2}}^{\text{T}}$， $\stackrel{⌢}{\Lambda }$ 为正对角矩阵，B为相应地缩放比例矩阵，且满足 $R^{-1}\text{d}u=B{R}^{\text{T}}\text{d}v$。我们可以选择常用的耗散算子 ${\stackrel{⌢}{\Lambda }}^{Roe}=\left|\Lambda \right|$， ${\stackrel{⌢}{\Lambda }}^{Rusanov}=\max \left|\Lambda \right|I$。

数值熵的耗散，尤其是间断附近的耗散。若熵产过多，间断附近会出现抹平现象；若熵产不足，间断附近会产生伪震荡。为构造恰当地数值耗散，Ismail和Roe [2] 对Euler方程的耗散算子做出了以下修改：

${\stackrel{⌢}{\Lambda }}_{EC1}=\left|\Lambda \right|+\frac{1}{6}\left|〚{\Lambda }_{u\pm a}〛\right|$， (2.13)

${\stackrel{⌢}{\Lambda }}_{EC2}=\left|{\Lambda }_{EC2}\right|+{\alpha }_{EC2}\left|〚{\Lambda }_{u\pm a}〛\right|$， (2.14)

其中

${\Lambda }_{EC2}=diag\left(\left(1+\beta \right)\left(u-a\right),u,\left(1+\beta \right)\left(u+a\right)\right)$， (2.15)

${\alpha }_{EC2}=\left({\alpha }_{\max }-{\alpha }_{\min }\right)\left(\max \left(0,sign\left(d{M}_{\max }-〚M〛\right)\right)\right)+{\alpha }_{\min }$。 (2.16)

这里 $〚M〛$ 代表通量交界面Mach数的改变， $〚{\Lambda }_{u\pm a}〛=diag\left(〚u-a〛,0,〚u+a〛\right)$。根据经验，选择 $\beta ={\alpha }_{\min }=\frac{1}{6},{\alpha }_{\max }=2.0,d{M}_{\max }=0.5$。

3. WENO-AO型重构

本文基于原始变量，在单元交界面处采用WENO-AO重构，获得左右高阶近似 $u_{j+\frac{1}{2}}^{-}$ 和 $u_{{}_{j+\frac{1}{2}}}^{\text{+}}$，分别代替原数值通量(2.11)中的 $u_j$ 和 $u_{j+1}$。进而得到WENO-AO型熵稳定数值通量为：

$f_{j+\frac{1}{2}}^{WENO-AO}=f_{j+\frac{1}{2}}^{EC}\left(u_{j+\frac{1}{2}}^{-},u_{j+\frac{1}{2}}^{+}\right)-\frac{1}{2}{D}_{j+\frac{1}{2}}\left(v_{j+\frac{1}{2}}^{+}-v_{j+\frac{1}{2}}^{-}\right)$ (3.1)

下面以 $u_{j+\frac{1}{2}}^{\pm }$ 中的 $u_{j+\frac{1}{2}}^{\pm }$ 为例，给出利用WENO-AO重构计算 $u_{j+\frac{1}{2}}^{-}$ 的方法 [4]，由对称性可得 $u_{j+\frac{1}{2}}^{+}$ 的重构过程。为了方便起见，定义 $\Delta u_j=u_{j+1}-u_j$。

首先，选定四个插值模板：

$\begin{array}{l}{S}_0=\left\{x_{i-3},x_{i-2},x_{i-1},x_i\right\},\\ S_1=\left\{x_{i-2},x_{i-1},x_i,x_{i+1}\right\},\\ S_2=\left\{x_{i-1},x_i,x_{i+1},x_{i+2}\right\},\\ S_3=\left\{S_0,S_1,S_2\right\}\end{array}$ (3.2)

其次，构造三个二次多项式和一个四次多项式：

$\begin{array}{l}\frac{1}{h}{\displaystyle {\int }_{x_{j-1/2}}^{x_{j+1/2}}{P}_{\text{0}}\left(x\right)\text{d}x}=\frac{\Delta u_j}{h},j=i-3,i-2,i-1,\\ \frac{1}{h}{\displaystyle {\int }_{x_{j-1/2}}^{x_{j+1/2}}{P}_1\left(x\right)\text{d}x}=\frac{\Delta u_j}{h},j=i-2,i-1,i,\\ \frac{1}{h}{\displaystyle {\int }_{x_{j-1/2}}^{x_{j+1/2}}{P}_{\text{2}}\left(x\right)\text{d}x}=\frac{\Delta u_j}{h},j=i-1,i,i+1,\\ \frac{1}{h}{\displaystyle {\int }_{x_{j-1/2}}^{x_{j+1/2}}{P}_3\left(x\right)\text{d}x}=\frac{\Delta u_j}{h},j=i-3,i-2,i-1,i,i+1\end{array}$ (3.3)

事实上，这些多项式在点 $x=x_j$ 的值给 $u_{j+\frac{1}{2}}^{-}$ 提供了三个三阶和一个五阶近似。经计算可得：

$\begin{array}{l}{P}_0\left(x_j\right)=\frac{1}{6h}\left(2\Delta u_{j-3}-7\Delta u_{j-2}+11\Delta u_{j-1}\right),\\ P_1\left(x_j\right)=\frac{1}{6h}\left(-\Delta u_{j-2}+5\Delta u_{j-1}+2\Delta u_j\right),\\ P_2\left(x_j\right)=\frac{1}{6h}\left(2\Delta u_{j-1}+5\Delta u_j-\Delta u_{j+1}\right),\\ P_3\left(x_j\right)=\frac{1}{60h}\left(2\Delta u_{j-3}-13\Delta u_{j-2}+47\Delta u_{j-1}+27\Delta u_j-3\Delta u_{j+1}\right)\end{array}$ (3.4)

从而可求得 $u_{j+\frac{1}{2}}^{-}$ 的重构方式为：

$u_{j+\frac{1}{2}}^{-}=\frac{{\omega }_3}{d_3}\left(P_3-d_0{P}_0-d_1{P}_1-d_2{P}_2\right)+d_0{P}_0+d_1{P}_1+d_2{P}_2$ (3.5)

WENO-AO重构的思想是：如果大模板 $S_3$ 是光滑的，则子模板 $S_0,S_1,S_2$ 必须是光滑的。在这种情况下，所有的平滑指标都有密切相似的值，从而 ${\omega }_0\to d_0,{\omega }_1\to d_1,{\omega }_2\to d_2,{\omega }_3\to d_3$。公式(3.5)意味着 $u_{j+\frac{1}{2}}^{-}\to P_3$，我们的格式在光滑区域达到五阶精度。如果大模板 $S_3$ 不光滑，有 ${\omega }_3\to 0$。公式(3.5)意味着 $u_{j+\frac{1}{2}}^{-}\to d_0{P}_0+d_1{P}_1+d_2{P}_2$，我们的格式退化到三阶CWENO重构。这样， $S_0,S_1,S_2$ 中最平滑的一个子模板将被寻找以避免伪振荡现象。

为了在(3.5)中完成 $u_{j+\frac{1}{2}}^{-}$ 的重构，需要计算权重 $w_i$，即

$w_j=\frac{{\alpha }_j}{{\displaystyle {\sum }_k{\alpha }_k}},{\alpha }_j=d_j\left(1+\frac{{\tau }^2}{\epsilon +I{S}_j}\right),j,k=0,1,2,3$ (3.6)

这里取 $\epsilon ={10}^{-12}$，以防止分母为零。对于模板 $S_0,S_1,S_2,S_3$，取线性权重为：

$\begin{array}{l}{d}_0=\left(1-d_c\right)\left(1-d_{cc}\right)/2;\\ d_1=\left(1-d_c\right)d_{cc};\\ d_2=\left(1-d_c\right)\left(1-d_{cc}\right)/2;\\ d_3=d_c\end{array}$ (3.7)

其中 $d_c,d_{cc}\in \left[0.85,0.95\right]$，且 $d_0+d_1+d_2+d_3=1$。

计算光滑性指标 $I{S}_i$，用来测量每个模板中所构造多项式的光滑性。

$I{S}_i={\displaystyle \underset{l=1}{\overset{r}{\sum }}{\displaystyle {\int }_{x_{j-1/2}}^{x_{j+1/2}}{h}^{2l-1}{\left(P_i^{\left(l\right)}\left(x\right)\right)}^2\text{d}x}},i=0,1,2,3$ (3.8)

当 $i=0,1,2$ 时， $r=2$ ；当 $i=3$ 时， $r=4$。即有：

$\begin{array}{l}I{S}_0=\frac{1}{4h^2}{\left(\Delta u_{j-3}-4\Delta u_{j-2}+3\Delta u_{j-1}\right)}^2+\frac{13}{12h^2}{\left(\Delta u_{j-3}-2\Delta u_{j-2}+\Delta u_{j-1}\right)}^2,\\ I{S}_1=\frac{1}{4h^2}{\left(\Delta u_{j-2}-\Delta u_j\right)}^2+\frac{13}{12h^2}{\left(\Delta u_{j-2}-2\Delta u_{j-1}+\Delta u_j\right)}^2,\\ I{S}_2=\frac{1}{4h^2}{\left(3\Delta u_{j-1}-4\Delta u_j+\Delta u_{j+1}\right)}^2+\frac{13}{12h^2}{\left(\Delta u_{j-1}-2\Delta u_j+\Delta u_{j+1}\right)}^2,\end{array}$

$\begin{array}{l}I{S}_3=\frac{1}{144h^2}{\left(\Delta u_{j-3}-8\Delta u_{j-2}+8\Delta u_j-\Delta u_{j+1}\right)}^2\\ +\frac{1}{15600h^2}{\left(-11\Delta u_{j-3}+174\Delta u_{j-2}-326\Delta u_{j-1}+174\Delta u_j-11\Delta u_{j+1}\right)}^2\\ +\frac{781}{2880h^2}{\left(-\Delta u_{j-3}+2\Delta u_{j-2}-2\Delta u_j+\Delta u_{j+1}\right)}^2\\ +\frac{1421461}{1310400h^2}{\left(\Delta u_{j-3}+4\Delta u_{j-2}+6\Delta u_{j-1}-4\Delta u_j+\Delta u_{j+1}\right)}^2\end{array}$ (3.9)

参数 $\tau =\frac{1}{3}\left(\left|I{S}_3-I{S}_0\right|+\left|I{S}_3-I{S}_1\right|+\left|I{S}_3-I{S}_2\right|\right)=O\left(h^4\right)$。

4. 数值实验

在本节中，给出了全离散格式获得的数值结果，并进行了比较。在时间方向上，采用三阶强稳定(SSP) Runge Kutta离散化方法 [5]。这种时间离散化的SSP性质在完全离散格式 [6] 的情况下，也以其凸性保持

了熵的稳定性。准确地说，保持了总熵 $E\left(t\right):={\displaystyle {\sum }_i\eta \left(u_i\left(t\right)\right)}$。三阶SSP Runge Kutta时间离散化方法为：

$\begin{array}{l}{u}^{\left(1\right)}=u^n+\Delta tL\left(u^n\right),\\ u^{\left(2\right)}=\frac{3}{4}{u}^n+\frac{1}{4}{u}^{\left(1\right)}+\frac{1}{4}\Delta tL\left(u^{\left(1\right)}\right),\\ u^{\left(n+1\right)}=\frac{1}{3}{u}^n+\frac{2}{3}{u}^{\left(2\right)}+\frac{2}{2}\Delta tL\left(u^{\left(2\right)}\right)\end{array}$ (4.1)

这里 ${\left(L\left(u\right)\right)}_i=-\frac{1}{h}\left({\hat{f}}_{i+\frac{1}{2}}-{\hat{f}}_{i-\frac{1}{2}}\right)$， ${\hat{f}}_{i\pm \frac{1}{2}}$ 为熵稳定数值通量(2.11)。

4.1. Burgers方程

$u_t+{\left(\frac{u^2}{2}\right)}_x=0$ (4.2)

间断初始条件：

$u\left(x,0\right)=\{\begin{array}{l}1,\left|x\right|\le \frac{1}{3}\\ -1,\frac{1}{3}\le \left|x\right|\le 1\end{array}$ (4.3)

对于初值为(4.3)的Burgers方程，其精确解包含左稀疏波和在点 $x=1/3$ 处的激波。从图1可以看出熵稳定格式(ES)在稀疏波出现间断，而WENO-AO型熵稳定格式(WENO-AO)可以精确捕捉到稀疏波，并且在激波附近无伪振荡产生，具有“高分辨率”的特性。

Figure 1. Solution of Burgers equation with initial condition (4.3) at t = 0.32 using 100 grids and CFL = 0.25

图1. Burgers方程，初始条件(4.3), N = 100, timeout = 0.32, CFL = 0.25

4.2. 一维Euler方程

我们使用两组初始数据求解Euler方程：

4.2.1. Sod激波管问题的初始值

$\{\begin{array}{l}\left({\rho }_l,u_l,p_l\right)=\left(1,0,1\right)x<0.5\\ \left({\rho }_r,u_r,p_r\right)=\left(0.125,0,0.1\right)x>0.5\end{array}$ (4.4)

Sod激波管问题是一个黎曼问题，初始间断分为左稀薄波、接触间断和右激波。我们采用Neumann边界条件，取CFL = 0.25，在空间区间[0, 1]上取200个网格点，计算T = 0.16时刻的解。即在扰动到达计算区域的边界之前的解。密度和内能的计算结果如图2所示。我们可以清楚地看到，WENO-AO型熵稳定重构可以更精确地捕捉到稀疏波、接触间断和激波，且没有振荡。

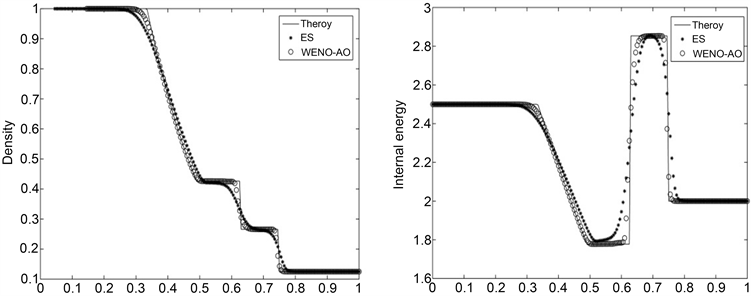
Figure 2. Solution of Sod’s shock tube test 1, N = 200, timeout = 0.14, CFL = 0.25

图2. Sod激波管问题的解，N = 200, timeout = 0.14, CFL= 0.25

4.2.2. Lax激波管问题的初值

$\{\begin{array}{l}\left({\rho }_l,u_l,p_l\right)=\left(0.445,0.698,3.528\right)x<0.5\\ \left({\rho }_r,u_r,p_r\right)=\left(0.5,0,0.571\right)x>0.5\end{array}\text{}$ (4.5)

Lax激波管问题是一个黎曼问题，解的密度和内能分布均由一个真正的非线性场(稀疏波、冲击波)和一个线性退化场(接触不连续性)组成。这种测试在高阶求解时具有挑战性，可能在接触间断和激波之间产生伪振荡。振荡是由解的第一阶段中波之间的相互作用引起的，当不连续性非常接近以至于算法找不到光滑模板时，可以对它们进行部分固化，用重构的方式实现波近似解耦。WENO-AO重构能够自动降阶，可以帮助减少振荡。结果如图3所示，在空间范围[0, 1]中取200个网格，使用ES格式和WENO-AO型熵稳定重构格式计算到T = 0.13时刻。观察到WENO-AO型熵稳定重构更精确地解决了平滑波，并在没有振荡的情况下快速捕捉冲击，具有较高的分辨率和更好的稳健性。

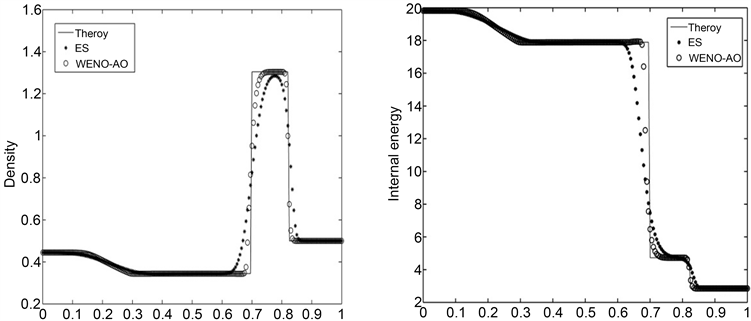
Figure 3. Solution of Lax’s shock tube test 2, N = 200, timeout = 0.14, CFL = 0.25

图3. Lax激波管问题的解，N = 200, timeout = 0.13, CFL = 0.25

5. 结语

本文以熵稳定格式为基础，通过在单元交界面处进行WENO-AO重构，建立了一种求解双曲守恒律方程的数值方法。通过Burgers方程和Euler方程的数值模拟可知，该格式具有分辨率高、捕捉能力强等特点。