1. 分级网格及其对偶网格的构造
对奇异摄动两点边值问题,由于小参数
的影响会产生边界层,普通的数值方法在均匀Shishkin网格上很难在靠近边界层处得到理想的数值解。为了得到奇异摄动问题稳定可靠的数值解,应要在其边界层区域放置比边界层外区域更多的网格点,以适应问题的奇异摄动特性。我们采用分级网格来解决边界层问题 [1] [2]。
根据奇异摄动边值问题的边界层,我们可分为以下三类,(1) 边界层存在于
两端点处,(2) 边界层存在于区间
的左端点,(3) 边界层存在于区间
的右端点。本文将着重分析边界层存在于区间
的左端点。
当边界层存在于区间
的左端点,将区间
划分为两个子区间
、
,每个子区间等分为
个网格点。调用参数
定义为:
.
这里
由边界层内网格的疏密程度决定,
是正的常数。比如可取
。N表示网格节点个数,且N是2的倍数。
是很小的正参数
。
其中网格节点定义为
网格的步长定义为:
我们对应的对偶分级网格点可以表示为:
其中对偶分级网格节点定义为:
对偶分级网格的步长记为
.
2. 基函数及空间构造
我们针对分级网格,可以得到相应的节点(不包括边界点)基函数如下:
同时,在对偶网格中对应内节点的对偶单元构造相应的分段常数基函数为:
定义线性有限元空间作为测试函数空间
,分段常数函数空间
作为检验函数空间,显然
。
3. 有限体积元方法及其格式
考虑如下线性奇异摄动两点边值问题 [3]:
(1)
其中
是很小的正参数
, 和
是已知量。假设在
上
是充分光滑函数。
和
是已知量。假设在
上
是充分光滑函数。
作如下变量变换,我们得到:
就可以将(1)化为如下齐次边界条件问题:
(2)
其中
。
对以上奇异摄动方程(2)对偶剖分中任意单元
上积分
(3)
上式具体可以写成
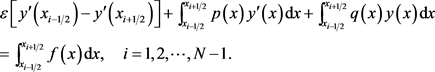 (4)
(4)
取相应的有限元
作y近似
(5)
由于
,所以满足
(6)
在区间
中,有
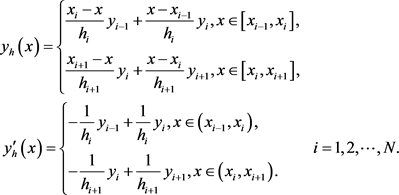
将表达式(6)代入(5),我们就可以得到一个关于
的线性代数方程组
(7)
注意,在边界上:
,令上式中的矩阵
其中
其中
则(7)式化为如下线性矩阵形式代数方程组
我们对以上的有限体积元方法的研究,有文献 [4] 可以得到了如下的结论:
定理3.1
是方程(2)的有限体积元解,在分级网格
的所有节点上
在分级网格
上,其超收敛性估计:
4. 数值例子
本小节给出如下数值例子来验证有限体积元法的有效性。
例题 考虑如下奇异摄动两点边值问题 [5]:
(8)
其精确解为
其中
。
微分方程(8)中
,对应的有限体积元格式为:
本例是左边界层,取
将区间
划分为两个子区间
、
,每个子区间等分为
个网格点。在分级网格下,网格节点为:

区间步长为:
对于相同的小参数
和剖分数N,针对不同的
值,得到分级网格的数值解,我们比较其与精确解的误差,如表1和表2。
通过表1和表2,我们可以看出,在分级网格的剖分下,数值解与精确解的误差相对来说较小。且当
越大,剖分精度越高,与精确解的误差越小。通过以上数据,我们可以得到,分级网格可以更好地计算边界层的数值解,靠近边界层处节点误差与其他节点的误差同阶。

Table 1. Finite volume element error when ε = 10 − 3 , N = 1000 , λ = 2
表1. 当
时的有限体积元误差

Table 2. Finite volume element error when ε = 10 − 3 , N = 1000 , λ = 2
表2. 当
时的有限体积元误差
基金项目
本文为国家自然科学基金项目(11571102)资助课题。