Gorenstein (m, n)-投射模

Gorenstein (m, n)-Projective Modules

摘要: 本文引入了Gorenstein (m, n)-投射模的概念。在强左(m, n)-凝聚环上研究了这类模的一些性质，并给出了Gorenstein (m, n)-投射模的一些等价刻画。

Abstract: In this article, the notion of Gorenstein (m, n)-projective modules is introduced. Some properties of such modules are investigated over strongly left (m, n)-coherent rings, and some equivalent characterizations of Gorenstein (m, n)-projective modules are given.

1. 引言

作为有限生成投射模的一种推广，Auslander和Bridger在文献 [1] 中研究了双边Noether环上Gorenstein维数为0的有限生成模。1995年，在文献 [2] 中Enochs和Jenda在一般环上引入Gorenstein投射模和Gorenstein内射模的概念。自此，以Gorenstein投射(内射)模为研究对象的Gorenstein同调代数受到了学者们的广泛关注 [1] - [6]。

2001年，作为n-内射模，P-内射模，FP-内射模的统一推广，Chen，Ding，Li和Zhou在文献 [7] 中引入了(m, n)-内射模的概念。2005年，Zhang等人在文献 [8] 中证明了在(m, n)-凝聚环上，(m, n)-内射左R-模的示性模是(m, n)-平坦的。同年，在文献 [9] 中，Mao和Ding在凝聚环上研究了模的FP-投射维数以及环的FP-投射整体维数。2006年，Mao和Ding在文献 [10] 中证明了 $\left(P_{m,n},I_{m,n}\right)$ 是完备的余挠理论，其中 $P_{m,n}$ 是(m, n)-投射模类， $I_{m,n}$ 是(m, n)-内射模类。2014年，曾月迪在文献 [11] 中引入强(m, n)-凝聚环的概念，并证明了在强(m, n)-凝聚环上， $\left(P_{m,n},I_{m,n}\right)$ 是完备遗传余挠对。2020年，杨强和赵仁育在文献 [12] 中研究了Gorenstein (m, n)-内射模，并在强(m, n)-凝聚环上利用Gorenstein (m, n)-内射模给出了左(m, n)-内射环的一些等价刻画。

受上述研究的启发，本文引入Gorenstein (m, n)-投射模的概念。证明了Gorenstein (m, n)-投射模关于直和封闭；在强左(m, n)-凝聚环和任意环上，给出了Gorenstein (m, n)-投射模的等价刻画。

2. 预备知识

设m和n是任取的两个正整数，R是具有单位元的结合环，所涉及的模均为左R-模。用 ${\text{id}}_R\left(M\right)$ 表示模M的内射维数，用 $\tilde{I}$ 表示所有内射维数有限的左R-模类，对于左R-模M，用 $M^{+}={\text{Hom}}_Z\left(M,Q/Z\right)$ 表示M的示性模。

定义2.1 称左R-模M是(m, n)-表示的，如果存在左R-模的短正合序列 $0\to K\to R^m\to M\to 0$，其中K是n-生成的。

定义2.2 称左R-模M是(m, n)-内射的，如果对任意的(m, n)-表示左R-模P， ${\text{Ext}}_R^1\left(P,M\right)=0$。

定义2.3 称左R-模N是(m, n)-投射的，如果对任意的(m, n)-内射左R-模M， ${\text{Ext}}_R^1\left(N,M\right)=0$ 。

注记2.4 (1) (m, n)-表示模是(m, n)-投射模；

(2) (m, n)-投射模关于直和，直和项和扩张封闭。

定义2.5 称环R是左(m, n)-凝聚环，如果左R-模 $R^m$ 的每一个n-生成子模是有限表示的。

定义2.6 称环R是强左(m, n)-凝聚环，如果 ${}_{R}R{}^m$ 的每一个n-生成子模是(m, n)-表示的。

3. Gorenstein (m, n)-投射模及其性质

定义3.1 称左R-模M是Gorenstein (m, n)-投射模，如果存在(m, n)-投射左R-模的正合序列

$\Im =\cdots \to P_1\to P_0\to P_{-1}\to P_{-2}\to \cdots$,

使得 $M=\mathrm{Im}\left(P_0\to P_{-1}\right)$，并对任意的 $E\in \tilde{I}\cap I_{m,n}$， ${\text{Hom}}_R\left(\Im ,E\right)$ 正合。

Gorenstein (m, n)-投射左R-模的类记为 $G{P}_{m,n}$。

注记3.2 (1) (m, n)-投射左R-模是Gorenstein (m, n)-投射左R-模；

(2) 若M是Gorenstein (m, n)-投射左R-模，则对任意 $E\in \tilde{I}\cap I_{m,n}$， ${\text{Ext}}_R^1\left(M,E\right)=0$ ；

(3) 若 $\Im =\cdots \to P_1\to P_0\to P_{-1}\to P_{-2}\to \cdots$ 是(m, n)-投射左R-模的正合序列，并对任意的 $E\in \tilde{I}\cap I_{m,n}$， ${\text{Hom}}_R\left(\Im ,E\right)$ 正合，则每个箭头的像，核，余核都是Gorenstein (m, n)-投射左R-模；

(4) Gorenstein (m, n)-投射左R-模关于直积封闭。

命题3.3 Gorenstein (m, n)-投射左R-模关于直和封闭。

证明 设 ${\left(M_i\right)}_{i\in \text{I}}$ 是一簇Gorenstein (m, n)-投射左R-模，令 $M={\oplus }_{i\in \text{I}}{M}_i$。对任意的 $i\in \text{I}$，因为 $M_i$ 是Gorenstein (m, n)-投射左R-模，所以存在(m, n)-投射左R-模的正合序列

${\Im }^i=\cdots \to P_1^i\to P_0^i\to P_{-1}^i\to P_{-2}^i\to \cdots$，

使得 $M_i\cong \mathrm{Im}\left(P_0^i\to P_{-1}^i\right)$，并对任意的 $E\in \tilde{I}\cap I_{m,n}$， ${\text{Hom}}_R\left({\Im }^i,E\right)$ 正合。于是有正合序列

${\oplus }_{i\in \text{I}}{\Im }^i=\cdots \to {\oplus }_{i\in \text{I}}{P}_1^i\to {\oplus }_{i\in \text{I}}{P}_0^i\to {\oplus }_{i\in \text{I}}{P}_{-1}^i\to {\oplus }_{i\in \text{I}}{P}_{-2}^i\to \cdots$，

使得 $M\cong \mathrm{Im}\left({\oplus }_{i\in \text{I}}{P}_0^i\to {\oplus }_{i\in \text{I}}{P}_{-1}^i\right)$，并对任意的 $E\in \tilde{I}\cap I_{m,n}$， ${\text{Hom}}_R\left({\oplus }_{i\in \text{I}}{\Im }^i,E\right)\cong {\Pi }_{i\in \text{I}}\left({\Im }^i,E\right)$ 正合。因此M是Gorenstein (m, n)-投射左R-模。

命题3.4 设R是强左(m, n)-凝聚环，M是左R-模，则以下成立：

(1) 若M是Gorenstein (m, n)-投射左R-模，则对任意的 $E\in \tilde{I}\cap I_{m,n}$，任意的 $i\ge 1$， ${\text{Ext}}_R^{\text{1}}\left(M,E\right)=0$ ；

(2) 对任意左R-模的正合序列 $0\to N\to G_{k-1}\to \cdots \to G_1\to G_0\to M\to 0$， $G_i\left(0\le i\le k-1\right)$ 是Gorenstein (m, n)-投射模，则对任意的 $E\in \tilde{I}\cap I_{m,n}$，以及任意的 $i>0$， ${\text{Ext}}_R^i\left(N,E\right)\cong {\text{Ext}}_R^{k+i}\left(M,E\right)$。

证明 (1) 设M是Gorenstein (m, n)-投射左R-模，E是(m, n)-内射左R-模，且 ${\text{id}}_R\left(E\right)=k<\infty$，考虑下列正合序列

$0\to M\to P_0\to P_1\to \cdots \to P_{k-1}\to P_0\to N\to 0$，

其中 $P_j\left(0\le i\le k-1\right)$ 是(m, n)-投射左R-模，因为R是强左(m, n)-凝聚环，由 [11] 定理2.2知 $\left(P_{m,n},I_{m,n}\right)$ 是完备遗传余挠对，所以 ${\text{Ext}}_R^{i\ge 1}\left(P_j,E\right)=0,0\le j\le k-1$。故对任意的 $i\ge 1$， ${\text{Ext}}_R^i\left(N,E\right)\cong {\text{Ext}}_R^{k+i}\left(M,E\right)$。又因为 ${\text{id}}_R\left(E\right)=k<\infty$，所以对任意的 $i\ge 1$， ${\text{Ext}}_R^i\left(N,E\right)\cong {\text{Ext}}_R^{k+i}\left(M,E\right)=0$。

(2) 的证明由(1)可得。

定理3.5 设R是强左(m, n)-凝聚环，M是左R-模，则M是Gorenstein (m, n)-投射左R-模当且仅当存在(m, n)-投射左R-模的正合序列

$\Im =\cdots \to P_1\to P_0\to P_{-1}\to P_{-2}\to \cdots$，

使得 $M=\mathrm{Im}\left(P_0\to P_{-1}\right)$。

证明 Þ)显然。

• )设N是(m, n)-内射左R-模，且 ${\text{id}}_R\left(N\right)=k<\infty$。下证 ${\text{Hom}}_R\left(\Im ,N\right)$ 正合，对k进行归纳总结。当 $k=0$ 时，结论显然成立。设 $k\ge 1$，考虑短正合序列

$0\to N\to E\to L\to 0$，

其中E是内射模， ${\text{id}}_R\left(L\right)=k-1$。则有短正合序列

$0\to L^{+}\to E^{+}\to N^{+}\to 0$，

因为R是强左(m, n)-凝聚环，由 [8] 定理5.7知， $E^{+}$ 和 $N^{+}$ 是(m, n)-平坦模，故 $L^{+}$ 是(m, n)-平坦模，再由 [8] 定理5.7知，L是(m, n)-内射模。由归纳假设知 ${\text{Hom}}_R\left(\Im ,L\right)$ 正合。于是存在复形的短正合序列

$0\to {\text{Hom}}_R\left(\Im ,N\right)\to {\text{Hom}}_R\left(\Im ,E\right)\to {\text{Hom}}_R\left(\Im ,L\right)\to 0$，

其中 ${\text{Hom}}_R\left(\Im ,E\right)$ 和 ${\text{Hom}}_R\left(\Im ,L\right)$ 正合，从而由 [13] 定理6.3知， ${\text{Hom}}_R\left(\Im ,N\right)$ 正合。因此M是Gorenstein (m, n)-投射的。

推论3.6 设R是强左(m, n)-凝聚环，M是左R-模，则以下等价：

(1) M是Gorenstein (m, n)-投射模；

(2) 存在左R-模的正合序列 $0\to M\to P_{-1}\to P_{-2}\to \cdots$，其中每个 $P_i$ 是(m, n)-投射模；

(3) 存在左R-模的短正合序列 $0\to M\to P\to L\to 0$，其中P是(m, n)-投射模，L是Gorenstein (m, n)-投射模。

证明 (1) Þ (3) Þ (2)显然。

(2) Þ (1)设 $\cdots \to P_1\to P_0\to M\to 0$ 是(m, n)-投射分解。由(2)知，存在左R-模的正合序列

$0\to M\to P_{-1}\to P_{-2}\to \cdots$，

其中 $P_{-1},P_{-2},\cdots$ 是(m, n)-投射左R-模，于是有左R-模的正合序列

$\cdots \to P_1\to P_0\to P_{-1}\to P_{-2}\to \cdots$，

使得 $M=\mathrm{Im}\left(P_0\to P_{-1}\right)$。故由定理3.5知M是Gorenstein (m, n)-投射模。

命题3.7 设R是强左(m, n)-凝聚环， $0\to M_1\to M_2\to M_3\to 0$ 是左R-模的短正合序列。则以下成立：

(1) 若 $M_1$ 是Gorenstein (m, n)-投射模， $M_3$ 是(m, n)-投射模，则 $M_2$ 是Gorenstein (m, n)-投射模；

(2) 若 $M_3$ 是Gorenstein (m, n)-投射模， $M_2$ 是(m, n)-投射模，则 $M_1$ 是Gorenstein (m, n)-投射模。

证明 (1) 因为 $M_1$ 是Gorenstein (m, n)-投射模，所以存在左R-模的短正合序列 $0\to M_1\to P\to N\to 0$，其中P是(m, n)-投射模，则N是Gorenstein (m, n)-投射模。考虑下列推出图1：

Figure 1. Pushout diagram

图1. 推出图

在短正合序列 $0\to P\to Q\to M_3\to 0$ 中，P和 $M_3$ 是(m, n)-投射模，由 [9] 注记2.8知，Q是(m, n)-投射模。在短正合序列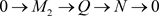中，因为N是Gorenstein (m, n)-投射模，所以由推论3.6知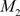，是Gorenstein (m, n)-投射模。

(2) 类似地，由推论3.6可得。

定理 3.8 设R环，则以下等价：

(1) 每个左R-模是Gorenstein (m, n)-投射的；

(2) 环R满足以下两个条件：

(i) 每个内射左R-模是(m, n)-投射的；

(ii) 每个内射维数有限的(m, n)-内射左R-模是内射的。

证明 (1) Þ (2) 设M是内射左R-模。则有(1)知M是Gorenstein (m, n)-投射模。于是存在短正合序列

，

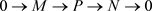其中P是(m, n)-投射模，由于M是内射模，所以该正合序列可裂。因此M是P的直和项，由注记2.4 (2)知，M是(m, n)-投射模。故(i)成立。设E是内射维数有限的(m, n)-内射左R-模，N是一个左R-模。由(1)知，N是Gorenstein (m, n)-投射模。于是由注记3.2 (2)知，，所以E是内射模，故(ii)成立。

(2) Þ (1) 设M是左R-模。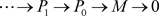是M的一个(m, n)-投射分解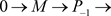，是M的一个内射分解，由(i)知存在(m, n)-投射左R-模的正合序列

，

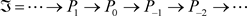使得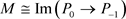。设E内射维数有限的(m, n)-内射左R-模，由(ii)知，E是内射模，所以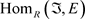正合。因此M是Gorenstein (m, n)-投射模。

基金项目

国家自然科学基金资助项目(11861055)。