叶轮结构参数改变对高比转速离心风机性能的影响

The Influence of Impeller Structure Parameters Change on the Performance of High Specific Speed Centrifugal Fan

摘要: 本文以T4-79 No.5风机为研究对象，采用数值模拟的方法，研究叶轮结构参数改变对处于高比转速工况的离心风机性能的影响。在原风机模型的基础上，分别改变叶轮的叶片数、轮径比、宽径比和出口安装角，通过数值模拟，对不同结构叶轮在高比转速工作区间进行了气动分析以及流动特性分析。结果表明：适当减少叶片数、增大轮径比、缩小宽径比有利于提高离心风机整机性能；随着出口安装角的减小，压力降低，效率增加，比转速变大，适合于高比转速工况运行。

Abstract: Taking the T4-79 No.5 fan as the research object, numerical simulation method is adopted to study the influence of impeller structural parameters change on the performance of the centrifugal fan under the condition of high specific speed. On the basis of the original fan model, the number of blades, the ratio of wheel diameter, the ratio of width to diameter and the outlet installation angle of the impeller were respectively changed. Through numerical simulation, the aerodynamic anal-ysis and flow characteristics analysis of the impeller of different structures in the working range of high specific speed were carried out. The results show that reducing the number of blades, in-creasing the ratio of wheel diameter and reducing the ratio of width to diameter are beneficial to improve the performance of the centrifugal fan. With the decrease of outlet installation angle, pressure decreases; efficiency increases; and specific speed increases, which are suitable for high specific speed operation.

1. 引言

离心风机是用于输送气体的机械，在国民经济的各个部门中应用广泛，特别是在化工、石油、能源、冶金和航空航天等领域，是主要的能耗设备之一 [1]。随着离心风机应用范围的拓展以及节能要求越来越高，部分常规系列的离心通风机已不能满足现场需求。经过大量调研，在大型工业系统如除尘、锅炉、排烟系统中，大量应用的4-72、4-73、4-79系列风机在运行时，处在大流量、低压头的情况，其运行比转速大致处于90~100的区间，部分风机比转速高达120，风机效率已低于70%，甚至更低，对于功率在1000千瓦以上的大型风机来说，能源浪费严重。例如某水泥厂窑尾除尘风机，测试进口流量806,000 m³/h，风机进口温度145℃，进口密度为0.8134 kg/m³，进出口全压3492 Pa，转速837 rpm，其运行工况比转速为108.1，运行效率61.3%。因此研究适合于大流量低压头的离心叶轮，使其在高比转速工况下运行也能有较理想的效率，也是工业节能的重要方向。

对于离心风机的研究，国内外已有显著的进展 [2] - [9]；而高比转速离心叶轮的研究，多集中于水轮机以及压气机，对于通风机领域的研究还相对较少。庞海宇等 [10] 在3-108离心风机的基础上进行了两次优化设计，总结出在大流量工况下，调整蜗壳与进风口可以改善流动损失。李轩等 [11] 对不同叶型的高比转速离心风机进行研究，结果表明在大流量工况下，板型叶片风机性能优于翼型叶片风机性能。Behzadmehr [12] 以数值模拟和实验相结合的方式，研究了后盘转子半径、入口半径、入口减速率等入口参数，对后向风机效率的影响，结果表明转子半径和其它参数的交互作用不明显，而其它参数的影响和彼此间的互相作用是十分显著的。王嘉冰等 [13] 的研究发现，不同的集流器形式可以导致风机内部流动状态有较大的变化，特别是锥弧形集流器，由于其喉部至叶轮进口的扩散段气流容易脱离壁面，导致边界层脱离而形成旋涡，使得叶轮流道内的流动情况恶化。阳诚武等 [14] 以前向叶片风机与后向叶片风机为基础，研究短叶片安装角度、短叶片周向位置、短叶片长度以及长短叶片数对风机整体性能的影响，结果表明：短叶片长度同时对两种形式风机的做功能力有较大影响，还会影响后向式风机的效率；短叶片的周向位置则对两种形式的风机的压力和效率均有重大的影响；短叶片安装角则对两种风机的性能影响都比较少。孙泳峰等 [15] 对带有封闭度为0.3、0.6、1的前盖板以及锥形前盘的离心风机进行数值模拟研究，结果表明在设计工况下，当封闭度为0.6时风机静压与全压均为最大，锥形前盘对于压力与效率的提高效果并不理想，并且在大流量工况下采用锥形前盘，会使风机的压力与效率下降。

T4-79系列为比转速较高的常用工业离心风机。本文以T4-79 No.5离心风机作为研究对象，其叶轮结构参数如图1所示，定义叶轮进口直径D₁与叶轮出口直径D₂之比为轮径比，叶轮出口宽度b₂与叶轮出口直径D₂之比为宽径比。在其它部件不变的情况下，改变叶轮的结构参数，包括叶片数、轮径比、宽径比、出口安装角，研究叶轮参数改变对风机在高比转速工况下运行时的影响规律，为今后高比转速离心风机设计提供参考。

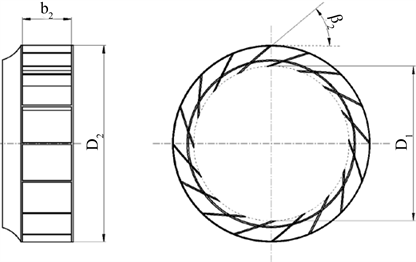
Figure 1. Diagram of centrifugal fan impeller

图1. 离心风机叶轮示意图

2. 高比转速离心风机的数值模拟

2.1. 动力学模拟基础模型建立

本文采用T4-79 No.5离心风机作为研究基础模型，如图2所示，基本参数如表1所示。

Table 1. Basic parameters of prototype fan

表1. 原型风机各项基本参数

应用Pro/E软件进行三维建模，然后对实体域模型进行布尔运算，得到对应的流体域。各模块采用统一接口定义，更改的模型可以共用其它模块。

表2给出了离心通风机模型在高效点下的网格无关性验证结果，从结果可以看出，当网格总数大于350万时，压力值变化不大，因此综合考虑计算资源以及精确度，选用第三组即400万网格作为计算模型。

在之后的研究中，依照此数量级为基础，对于每一个新类型模型进行在400万网格左右进行总共3次的无关性验证。

Figure 2. Prototype fan model

图2. 风机基础模型

Table 2. Grid independence validates data

表2. 网格无关性验证数据

2.2. 数值计算方法

采用CFD-FLUENT对风机内部流场进行数值模拟。计算时采用三维雷诺时均守恒Navier-Stokes方程。湍流模型采用标准k-ε模型，计算方法采用SEGREGATED隐式方法，压力–速度耦合采用SIMPLE算法，湍动能、湍流耗散项及动量方程采用二阶迎风格式离散 [16]。

其中湍流动能k及湍流耗散率ε的输运方程为：

$\frac{\partial \left(\rho k\right)}{\partial t}+U_i\frac{\partial \left(\rho k\right)}{\partial x_j}=\frac{\partial }{\partial x_j}\left(\frac{{\mu }_t}{{\sigma }_k}\frac{\partial k}{\partial x_j}+\mu \frac{\partial k}{\partial x{}_j}\right)+{\mu }_t\left(\frac{\partial U_i}{\partial x_j}+\frac{\partial U_j}{\partial x_i}\right)\frac{\partial U_i}{\partial x_j}-\rho \epsilon$ (1)

$\frac{\partial \left(\rho \epsilon \right)}{\partial t}+U_i\frac{\partial \left(\rho \epsilon \right)}{\partial x_i}=\frac{\partial }{\partial x_j}\left(\frac{{\mu }_t}{{\sigma }_{\epsilon }}\frac{\partial \epsilon }{\partial x_j}+\mu \frac{\partial \epsilon }{\partial x_j}\right)+C_{1\epsilon }{\mu }_t\frac{\epsilon }{k}\left(\frac{\partial U_i}{\partial x_j}+\frac{\partial U_j}{\partial x_i}\right)\frac{\partial U_i}{\partial x_j}-\rho C_{2\epsilon }\frac{{\epsilon }^2}{k}$ (2)

湍流黏度：

${\mu }_t=\rho C_{\mu }{k}^2/\epsilon$ (3)

式中： ${\sigma }_k$ 和 ${\sigma }_{\epsilon }$ 为湍动能k和耗散率ε对应的Prandtl数， $C_{1\epsilon }$ 、 $C_{2\epsilon }$ 、 $C_{\mu }$ 为经验常数。

由于模型中同时存在动网格区如叶轮，以及静网格区如蜗壳，因此叶轮选用旋转坐标，蜗壳、集流器等选用静止坐标，旋转区域与静止区域间采用MRF——多重参考系模型进行耦合，即用稳态方法计算非稳态问题。气流在风机中做不可压缩流动，并忽略重力对流场的影响 [17] [18]。进口边界条件采用质量流量进口，出口设置为自由出口。壁面采用无滑移边界条件，近壁区域采用标准壁面函数。

2.3. 可靠性验证

根据于洪 [19] 提供的4-79 No.5系列风机性能数据及介绍，与本文基础模型风机的模拟数据进行对比，验证基础模型的可靠性，将模拟结果与理论值绘制成如图3所示性能曲线。由图可知计算模拟值与理论的趋势基本一致，其效率值最大偏差均在2%以内，从而验证了本文所采用的数值计算模型及方法的可靠性。计算模型略低于理论值，是因为计算模型做了一些简化以及耦合方程本身带来的一些误差及损失 [20]。

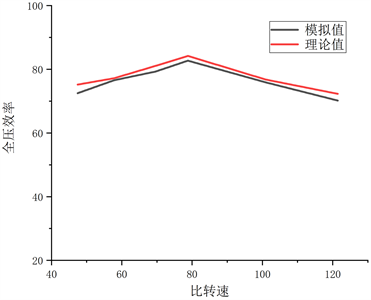
Figure 3. Comparison of prototype model performance curve

图3. 原始风机性能曲线对比

3. 高比转速工况下叶轮结构参数改变结果分析

叶轮是离心风机的核心气动部件，叶轮损失也是整个风机损失的主要来源，当叶轮处于偏离设计工况，即在高比转速工况下运行时，此时叶轮内部流动更加复杂，流动损失加大。因此若想提高高比转速工况下离心风机性能，对叶轮结构参数的研究意义重大。本文拟改变叶片数、轮径比、出口安装角、宽径比，而其它结构不变，研究高比转速工况离心风机的性能变化规律。

3.1. 叶片数对高比转速离心风机性能的影响

叶片数是决定风机气动性能的主要参数之一，叶片数过多会使气流的有效通流面积减小，导致叶轮入口的冲击损失以及沿程摩擦损失加剧，风机全压和效率下降。而叶片数过少则会加剧二次涡流的形成。在高比转速工况下，流量急剧增大，流动阻塞以及叶片与气流的沿程摩擦将成为主要流动损失，因此在考虑调整叶片数时，叶片数应适当减少。在其它条件不变的情况下，仅改变叶片数，研究其对离心风机性能的影响。原风机模型叶片数为Z = 16，拟选取叶片数Z = 14、Z = 12、Z = 10、Z = 8、Z = 6，并分别重新建立模型，并进行数值模拟计算。

叶片附近是气流变化最为剧烈的部位，网格的分布也最为密集，因此在对叶轮叶片数讨论过程中，由于叶片周围存在复杂流动，因此需要重新进行网格无关性验证，其结果如表3。为了节约计算资源，选择230万网格数作为6~10叶片叶轮模型的网格数量。

Table 3. Verification of grid independence of 8-blade impeller

表3. 8叶片叶轮网格无关性验证

图4为不同叶片数模型的无因次性能曲线。叶片数为10~14的模型中，高比转速区域的静压效率平均高于原模型约3%~5%。而6、8叶片模型在高比转速区域也有不低的静压效率，且在区间内较原模型高5%~8%。

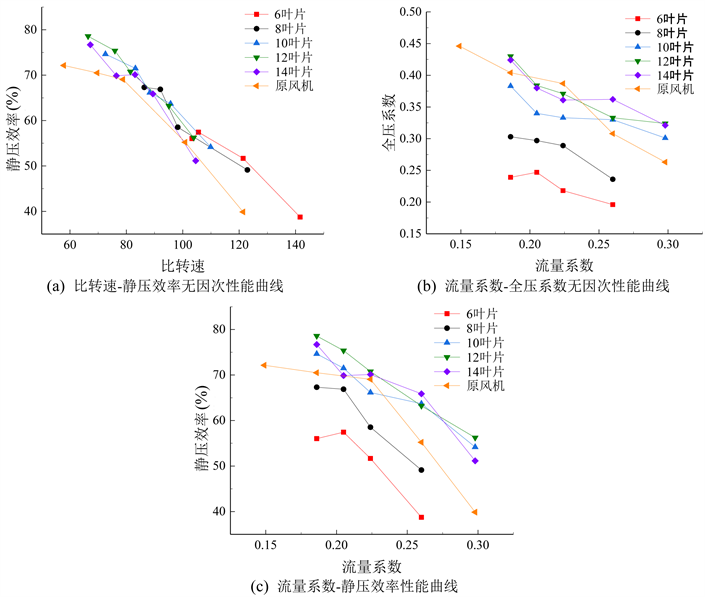
Figure 4. Performance curve of different blade numbers

图4. 不同叶片数性能曲线

在同一流量区间内，随着叶片数的减少，压力随之减小，10叶片以下压力减小速度明显变大。在大流量系数区间，随着叶片数的减少，风机压力降低明显，而风机比转速变大，并且叶片数越少，对应比转速越大，静压效率曲线越平缓。叶片数6~12时，在流量区间内压力降低，但其效率均有所提升，说明在流量区间内，压力下降适合于提升静压效率，特别是在高比转速区间(90~110)，以叶轮在高比转速工况下的高效率为目标，需要在原基础上减少叶片数。

如图5为不同叶片数叶轮在流量系数为0.26时的50%叶高速度云图。由图可知，随着叶片数的减小，流道越来越大，叶片吸力面流动分离趋势逐渐增加，叶片入口低速流体逐步向叶轮径向扩展，因此，随着叶片数的减少，流道内扩压度增大，气流离开叶轮落后角增加，平均速度下降，导致压力降低。但由于叶片少，阻塞程度下降，叶轮的通流能力显著提升，利于大流量工况运行，仅需合理控制流道内的流动分离损失。

显然，叶片数降低，叶片流道的相对通流能力增大，意味着该类流动特点适合于大流量的流动，即离心风机的高比转速运行工况。

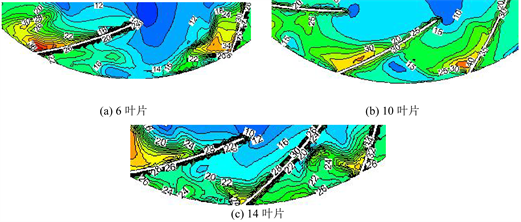
Figure 5. 50% high speed cloud chart with different number of blades

图5. 不同叶片数50%叶高速度云图

3.2. 轮径比对高比转速离心风机性能的影响

叶轮进出口直径D₁和D₂的确定原则为叶道内的流动损失最小，由于流动损失与叶片进口相对速度的平方成正比，可知进口相对速度越小，损失越小。如果进口直径过大，则圆周速度增大，导致气流进口相对速度很大；如果进口直径过小，但径向速度会因为进口截面积的减小而增大，使得相对速度很大。因此对于轮径比，必须选择一个合适的值。目前轮径比D₁/D₂的确定一般采用推荐值，但是在本文所研究的高比转速工作区间，进口相对速度必然增大，损失也会增大。因此考虑改变进口直径时，讨论其进口损失及流道变化对整机效率的影响。

以原型风机轮径比D₁/D₂ = 0.704为基础，将其缩放为原来的0.94、0.97、1.03、1.06、1.09、1.12倍，并与原型进行对比，以经济性原则考虑，不改变叶轮出口直径以匹配其它部件，即D₂ = 500 mm不变，依照轮径比改变D₁的大小。

如图6为不同轮径比叶轮性能曲线。由图6(a)可知随着轮径比的增大，在比转速为90~110的区间，1.06倍轮径比的静压效率曲线最高，较原模型提升3%左右，同时变化趋势也最平缓。轮径比减小时，在低比转速区域可以较为明显的提高风机性能，静压效率提升了7%，但同时也会导致比转速覆盖范围变小。而其余不同轮径比的模型，特别是在比转速为100及以上的工况区间，效率较原始模型提升不明显，甚至低于原始模型。

由图6(b)可知，当轮径比增大时，在流量系数为0.26之后的区域可以发现出现了曲线间断的现象，1.03倍轮径比曲线尤为明显，此时压力升高，性能曲线不连续，为风机大流量工况的断裂点。断裂点通常出现在大流量区间，此时蜗壳内部流动复杂，形成大量涡流，出现断裂点，导致性能曲线不连续。

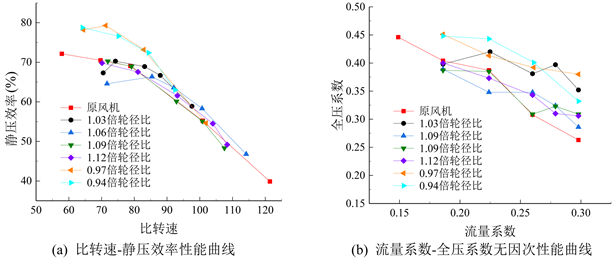
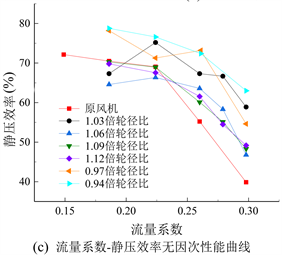
Figure 6. Performance curve of different wheel diameter ratio

图6. 不同轮径比性能曲线

图7分别为1.06、1.09、1.12倍基础风机模型轮径比的180˚子午面速度流线图。随着轮径比增大，叶片逐渐缩短，气体在流道内没有得到充分发展，导致二次流加剧，特别是1.09~1.12倍轮径比模型，在流道间产生了巨大的漩涡，造成了很大的流动损失。表明在高比转速工作区间，流量偏大，增大轮径比虽然可以在一定程度上减小流动损失及摩擦损失，但是二次流的发展也会使损失加剧，因此选择一个适合的轮径比仍比较重要。

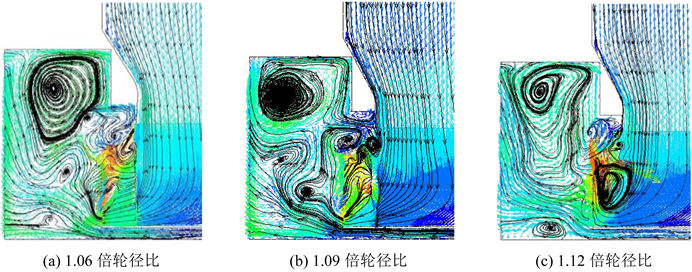
Figure 7. 180˚ meridian plane velocity streamline diagram with different wheel diameter ratio

图7. 不同轮径比180˚子午面速度流线图

3.3. 宽径比对高比转速离心风机性能的影响

对于宽径比b₂/D₂，当其它设计参数不变时，宽径比增大带来出口角减小，叶片出口宽度增大。前者有利于效率提高，后者却会导致叶轮通道扩压度增大，引起分离 [21]，并且会使压力上升，在高比转速工作区间，为大流量、低压头的工作环境，不能一味增大宽径比。为了研究宽径比改变对高比转速工况离心风机的性能变化规律，在原宽径比基础上，维持风机出口直径D₂不变，增大出口宽度b来改变宽径比，分别取原风机宽径比的0.92倍、0.96倍、1.04倍、1.08倍、1.12倍，进行建模及数值模拟。

如图8分别为不同宽径比下的性能曲线。由图可知，宽径比减小，在流量考核范围内，压力变化不大，因此比转速变化也不大，但是静压效率升高；0.92倍宽径比时静压效率曲线分布处于最上方。

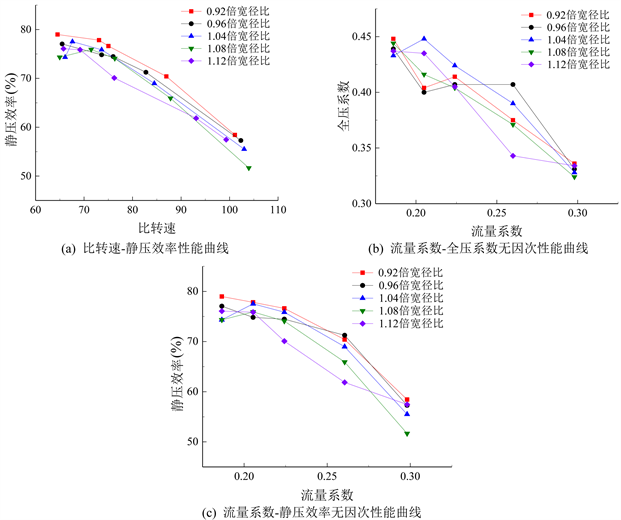
Figure 8. Performance curve of different width diameter ratio

图8. 不同宽径比性能曲线图

图9为0.96倍、1.08倍、1.12倍宽径比的离心风机模型，在流量系数为0.26，比转速均处于90附近的180˚子午面总压–流线图。由图可知，在叶轮流道内，随着宽径比的增大，二次流造成的影响逐渐增大；1.08倍宽径比时，仅在叶高50%处附近产生了一定程度的阻塞，而1.12倍宽径比时，则在50%以上部分均有不同程度的阻塞，并且形成了明显的回流，说明宽径比过大在高比转速工况下会导致边界层分离加剧。而在蜗壳通道，随着宽径比的增大，可以发现蜗壳通道内无论是涡的数量还是剧烈程度，均有明显改善，降低了流动损失。

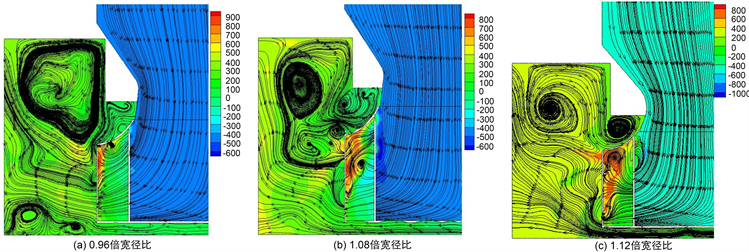
Figure 9. Flow line diagram of total pressure at 180˚ meridian with different width diameter ratio

图9. 不同宽径比180˚子午面速度流线图

3.4. 出口安装角对高比转速离心风机性能的影响

在后向式叶轮中，在合理的范围内，随着出口安装角的增大，流量-压力性能曲线会向右上方移动，出口安装角过度增加，又会使全压中的动压比例升高，增大流动的扩散度导致效率下降。为了探究在高比转速区间不同出口安装角叶轮的风机性能，在基础模型出口安装角β₂为39˚的基础上，取β₂ = 36˚、42˚、45˚、48˚，对叶轮建模，并划分网格，与其余各部分流体域组合后进行数值模拟计算。

图10为不同出口安装角下离心风机的性能曲线。由图可知，随着出口安装角的增大，压力升高，使新模型性能曲线的最佳工况点快速左移，向低比转速方向移动；出口安装角减小时，可以发现其性能曲线较其他曲线明显处于上方，在比转速覆盖区域差别不大的情况下，静压效率较高。同时结合两图可以看出，出口安装角的变化，并不会使比转速的覆盖范围产生明显的变化。

根据叶片出口安装角的变化，可以看出，随着叶片出口安装角的降低，压力降低，比转速变大，性能曲线向高比转速方向移动，且效率有所提高。

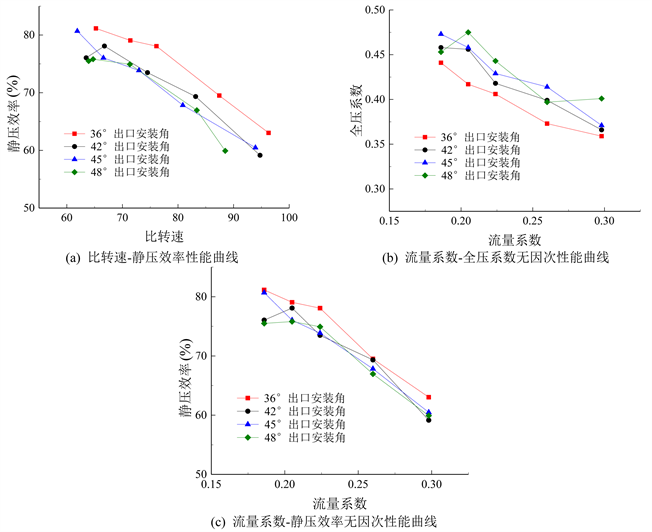
Figure 10. Performance curve of different outlet installation angles

图10. 不同出口安装角性能曲线图

4. 结论

通过以上数值模拟及分析，可以得到如下结论：

(1) 随着叶片数的减少，大流量系数区间风机静压及全压下降，比转速变大，静压效率曲线平缓。在高比转速区域，6~12叶片性能曲线均优于原模型，适当降低叶片数可以减小摩擦损失及流动损失，叶片流道的相对通流能力增大，即这种流动特性适合于离心风机的高比转速运行工况。

(2) 轮径比增大，在高比转速工作区间的性能曲线逐渐变平缓，轮径比为原风机的1.06倍时，高效工况点均处在比转速为90~110的高比转速区间，相较与原始模型，在该高比转速区间，平均静压效率提升了3%以上。

(3) 当宽径比为原风机的0.92倍时，静压效率曲线较其它宽径比模型平均增大了2%~3%，适当缩小宽径比有助于提高整机性能；宽径比的改变对于比转速的覆盖范围并无明显的影响。

(4) 叶片出口安装角的变化对离心风机的影响为：随着出口安装角的减小，压力降低，效率增加，比转速变大，适合于高比转速工况运行。