1. 引言
大学数学通识课包括高等数学、线性代数、概率统计以及复变函数等一些基本课程,大学数学通识课是理工科学生必备的知识基础 [1] [2]。通过大学数学通识课的学习,学生不但可以掌握基础知识,为以后进一步学习奠定基础,同时,通过数学通识课的学习,还可以培养学生良好的思维品质,提高学生分析问题、解决问题的能力。传统教学以讲授为主,这种教学方式的优点是信息量大,系统性强,便于完成教学任务。课堂教学一般分三步走:概念、定理、例题与练习。这种方式便于提高学生的解题能力,但不利于培养学生解决实际问题的能力。另外,在这种教学模式下,学生被动学习,无法调动学生的学习兴趣,严重影响创造力的发挥,教学模式的改革势在必行。
数学以理论为基础,但最终为实践服务。将理论应用于实际,这是学习的目的,也应该是我们教学的着眼点 [3] [4]。为进一步提高学生利用数学解决实际问题的能力,提高学生学习兴趣,在大学数学的教学过程中引入数学实验已成为现代教学的发展趋势 [5] [6] [7] [8]。在课堂上融入数学实验,可以提高学生的主体意识,提高学生学习数学的趣味性,让学生不但会学、而且会用数学。在大学数学教学过程中开展实验教学的研究,适应当代社会对大学生的培养要求,促进学生身心发展,是以人为本的科学发展观在高校数学教学中重要体现。如何结合高校数学通识课的特点,将数学实验循序渐进、高效地引入到高等数学教学中是一个值得研究和探讨的问题。本文结合大学数学教学实践,提出对如何更好将数学实验融入到大学数学教学的一些认识和思考。
2. 数学实验融入大学数学教学的具体举措
2.1. 教材撰写时每章节增加数学实验内容
Matlab是一款应用广泛、功能强大的数学软件。利用Matlab可以求微分方程、线性方程组的解,进行随机模拟,画图,另外Matlab中还有许多可以直接调用的函数和解决比较复杂问题的功能模块,例如优化模块、时间序列模块等等。在教材的每一章节之后适当的添加相应的数学实验内容,便于学生借助数学软件探究本章知识内容、深化对所学知识的认识,也有利于学生利用所学数学知识去解决实际问题。现在有越多越多的教材都非常重视增加数学实验的内容。例如在2011年1月郭跃华、朱月萍主编的《概率论与数理统计》教材每一章节中,都增加了数学实验内容 [9]。再如2006年蔡瑞胸编著的《金融时间序列分析》教材不但介绍计量经济学和统计学的基础理论和方法,另外还大量介绍了金融时间序列分析的最新进展,强调实例和数据分析 [10]。在大学数学课程中融入数学实验内容是现代教学的发展趋势。
2.2. 借助数学实验推进过程教学
1) 借助Matlab介绍抽象概念,加深学生理解
大学数学里有许多抽象的知识,直接介绍,学生接受比较困难,不利于学习的进一步深入 [11]。借助于Matlab的绘图功能,便于展示抽象概念的本质特征,使学生对概念有比较直观的认识,既能提高学生学习的兴趣,又可以增加学生对概念的理解和记忆,降低学习的难度。
案例1 《高等数学》上册空间解析几何一章介绍了空间点坐标与卦限关系。如果死记非常困难,用Matlab将空间直角坐标系画出来,对照图形,先分析每个卦限中点的坐标特征,然后再加以记忆,就很容易把握这部分内容。绘制空间直角坐标系命令如下:
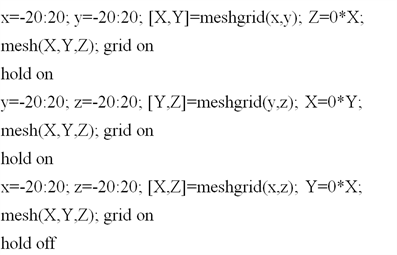
运行该程序,可以得出空间直角坐标系(图1)。结合图1对每个卦限的点坐标进行分析,就很容易掌握点坐标和卦限的对应关系。
案例2 空间曲面及其方程。
空间曲面可以用方程来刻画,常见空间曲面包括旋转曲面、柱面等。大部分学生空间想象能力还是缺乏的,难以由一个方程联想到相应的空间图形,因而很难进一步把握空间图形的性质。借助Matlab,画出相关图形,结合图形对照讲解,可以创造学习情境、激发学生学习兴趣、降低学生学习难度。运行如下Matlab命令,可得图2和图3。
从图2和图3中,不难看出曲线在旋转过程中到旋转轴的距离是不变的,而动直线沿着准线移动形成柱面,柱面的母线是一组平行直线等等。用Matlab绘图,可以教会学生用实验的方法研究抽象的概念,化难为易。此外,定积分的概念、《概率理与数理统计》中许多重要的概念借助于Matlab中绘图功能既可以深化学生对概念的认识,也有助于学生在后续处理实际问题时,能够通过图形迅速判断出数据的统计特征:如在概率统计分布函数教学过程中利用Matlab展示常见分布函数的图像,学生在后续数据处理时,可以反过来根据分布曲线的特征,选用合适的拟合曲线。
2) 借助数学实验,揭示重要数学规律
数学中有许多定理非常抽象,借助数学实验,容易揭示数学规律,有助于对定理形成深刻的认识。
案例3 函数单调性、凹凸性以及极值和拐点判别方法。
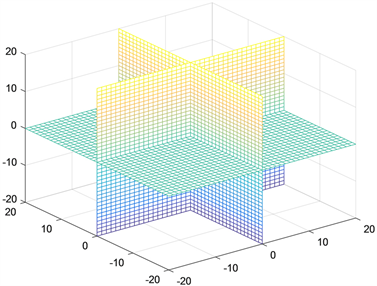
Figure 1. The coordinate system of right angle of the space
图1. 空间直角坐标系
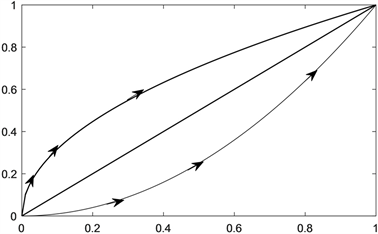
Figure 4. The curves with properties of monotonicity and convexity
图4. 曲线单调性凹凸性图
这一部分判别方法基本都以定理形式呈现,定理中,一阶导数、二阶导数被用来判别函数单调性、凹凸性以及求极值点和拐点。书上归纳了好几个定理,不容易记忆 [12]。事实上,在进行这部分教学时,我们可借助于Matlab绘制函数图像进行观察。例如输入一下命令可得图4。
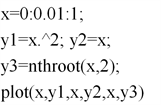
图4中的几条曲线,尽管凸凹性不同,但都是单调增的,此时一阶导数都大于0,因此单调增(减)跟一阶导数有关:一阶导数大于等于0,单调增,一阶导数小于等于0,单调减。凹凸性则跟二阶导数值有关,二阶导数小于等于0,曲线凸,反之,曲线凹。再如在高等数学二重积分、三重积分、第一型曲面积分、第二型曲面积分教学中利用数学实验展现微元法思想,既可以降低学生学习难度,还可以提高学生学习效率。同样,概率统计中的许多抽象的性质定理例如频率和概率的关系,大数定律等,借助 Matlab设计实验进行教学,可以给学生留下深刻的印象,使得其对知识的理解更为深刻。
3. 结语
在大学数学教学中,我们要注意不但让学生会学,还要让学生会用。数学实验可以提高学生的学习兴趣,可以使学生在探讨的过程中对知识有更深刻的理解,使学生养成良好的科学思维品质,为以后学习或进一步深造打下坚实的基础。
致谢
感谢淮安市自然科学基金(HABZ202019)的资助!