1. 引言
《应用数学》课程是士官必修的任职基础课程,课程以“必须、够用”为准则制定了教学目标与教学内容 [1]。课程教学内容多、教学要求高、学员数学基本功差等都加剧了教学的难度。课程以BOPPPS教学法为依据,改变教学模式,形成“填鸭–预习–评价”三位一体的教学模式,意在迅速提高士官知识起点,更好地完成教学目标,完成“脑力马拉松”,训练意志力,有效培养士官学员的数学素养。
BOPPPS注重以学员为中心,充分发挥学员的主动性,重视学员的参与和反馈,注重教学互动和反思,从而更有效地得到良好的教学效果。BOPPPS模型将教学过程划分为导入–学习目标–前测–参与式学习–后测–总结六个阶段 [2]。但是由于军队院校的特殊性,以及教学对象本身的矛盾,即学员起点低、思维方式单一以及知识管理弱等,照搬模式并不适用,并且会在很大程度上影响教学效果。本文将在此模型的基础上进行改进,变成“‘填鸭’补充–前测–导入–学习目标–参与式学习–后测–总结”模式,以案例来呈现其合理性。
2. 寻找教学起点,实现BOPPPS教学模式与应用数学教学相结合
士官学员来源广泛且基础层次不齐,为明确教学起点,更有针对性的实施教学,会进行学前摸底测试。测试包含14%的小学内容,70%的初中内容,以及16%的高中内容,表1可直观反映出学员成绩两极分化大,并无坚实的数学基础支撑。
大部分学员认知基础差、思维方式是典型的点线性思维(图1),知识管理差,抽象思维弱,知识之间无法产生联系、迁移。少数是类网状思维(图2),可以在几个类似的知识点间形成网状管理形成闭环,这部分学员基础好,抽象思维较强,可以进行横向迁移。
由此可以看出,大部分学员不具备大专层面的数学基础,难以支撑学习应用数学 [3]。因此,在BOPPPS教学模式下,增加“填鸭”补充将前测环节前置,即在学习之前,要对必须的数学知识进行“填鸭式”循环补充,达到学习应用数学的起点。
对于抽象思维弱、难以接受复杂概念的现象,要合理的设计课堂环节,尽量让学员从已知或者可观察的方面,自己总结概括概念定理,实现以教员单纯“讲授”转变成学员主动“学习”,见图3。除此之外,增加学员课后相互评价并讲解的过程,更加有利于激发学员的学习兴趣。值得注意的是,学员层次差距大,因此在保证大多数学员都能达到教学目标的情况下,也要注意分层次的教学。
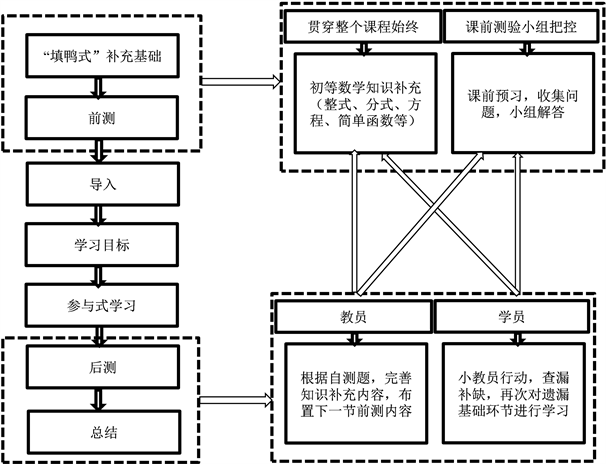
Figure3. Combined with BOPPPS and Applied Mathematics
图3. BOPPPS模式与应用数学相结合
3. 基于BOPPPS教学模式与应用数学结合下的课堂案例
数列的极限是上承数列,下接函数的极限,是连接常量数学与变量数学的桥梁。“极限”是现代数学的基本思想方法,贯穿了整个应用数学的始终,数列的极限是极限理论中最简单的一部分,是对数学世界认识从有限到无限的敲门砖。但是内容的理解上有一定的难度,因此,对学员的知识掌握上的要求是能够阐述数列极限的概念并且会用数列的极限的四则运算求解简单的极限问题,下表2是基于BOPPPS教学模式下的课堂设计。

Table 2. Limit of the sequence’ teaching design
表2. 数列的极限的课堂设计
4. 总结与反思
本文基于BOPPPS教学模型给出了一节课数列的极限的教学设计,但是模型不能机械的套用,而是应该以学员的实际情况,及时作出调整。根据学员特点,增加了“填鸭”补充基础阶段以及将前测部分提前,这样就可以给教员课堂依据,及时调整内容。“填鸭”补充应有的知识结构是“速成法”,其更多的是依赖学员的学习自觉性,而这恰恰正是学员缺少的,这样会导致学员基础不牢固,因此需要“小教员”协助。明确在课程教学目标中,让学员知道这部分知识的用处,增加学员的学习积极性,而不是单纯的三维目标,从而达到较好的课堂效果。