圆管内置不同形状涡产生器管内流动特性的数值分析

Numerical Study of the Flow Characteristics in a Circular Tube Fitted with Different Shape Vortex Generator

摘要: 圆管内置涡产生器是一种被动式的强化传热方式。涡产生器在管内诱导产生的二次流是强化传热的主要原因，而二次流强度受制于流动参数和涡产生器的结构参数。本文采用数值方法对圆管内置不同形状涡产生器的流动特性进行了研究。研究结果表明：不同形状涡产生器在圆管内产生的平均二次流强度和沿流动方向的局部二次流强度依次为等腰梯形涡产生器最强，直角梯形涡产生器次之，矩形涡产生器最弱；在传统扭带基础上裁除材料面积相同的条件下，涡产生器形状对管内流体的平均阻力系数和沿流动方向的局部阻力系数影响甚微。对比不同位置的二次流强度云图发现，与基带处相比，涡产生器在圆管内诱导产生了更强的二次流。内置不同形状的涡产生器后，管内流体的二次流强度分布和流线分布发生变化，与其余三种形状的涡产生器相比，等腰梯形涡产生器诱导产生的二次流更强。

Abstract: The vortex generator inserted into a circular tube is a passive heat transfer enhancement method. The secondary flow induced by the vortex generator in the tube is the main reason for the heat transfer enhancement, and the intensity of secondary flow is subject to flow parameters and the structural parameters of vortex generators. In this paper, the numerical method is used to study the flow characteristics of the different shapes vortex generators inserted into the circular tube. It is found that the average secondary flow intensity and the local secondary flow intensity along the flow direction generated by the vortex generators with different shapes are the strongest in the order of isosceles trapezoidal vortex generators, followed by right-angle trapezoid vortex generator and the weakest in the rectangular vortex generator. When the geometric area of material cut from the traditional twisted tape to form different vortex generator inserts is identical, the shape of vortex generator has little influence on the average friction factors and the local friction factors along the flow direction. By comparing the secondary flow cloud graphs at different locations, it is found that compared with the baseband, the vortex generator induces stronger secondary flow in the tube. When vortex generators with different shapes are built in, the secondary flow intensity distribution and streamline distribution of the fluid in the tube change. Compared with the other three vortex generators with different shapes, the isosceles trapezoidal vortex generator can induce stronger secondary flow.

1. 引言

管内插入扰流元件是常见的管内强化换热技术，因为其成本相对较低，工艺简单，方便制造和安装，并且可以有效地抑制污垢生成，有利于旧换热器的改造，所以在工程技术领域得到了广泛使用 [1]。扭带是结构最简单的内插扰流元件，其强化传热的主要机理是扭带诱导管内流体产生了二次流，使得流体的流动方向发生了变化。二次流是指垂直主流方向平面上的流动，通常比主流速度小一个数量级，但可以明显强化对流传热，又不会过多地引起流动机械能的耗散，其主要原因是壁面上的阻力损失主要取决于主流在壁面法向方向的速度梯度，而不取决于二次流的梯度 [2]。由于扭带在管内强化换热上取得的良好效果，学者们对二次流强度和对流换热的影响因素开展了广泛研究。Rindt等 [3] 对Re = 500，Pr = 5时，壁温随轴向变化的螺旋盘管换热器的混合对流发展进行了研究，并与恒定壁温边界条件进行比较，分析了浮力对传热和二次流的影响。为了明确斜肋的流体流动结构及其对轴向传热分布的影响，Robert等 [4] 对斜肋诱导产生二次流进行了实验和数值模拟，明确地证明了斜肋比传统横肋具有传热优越性。Pankaj等 [5]、Sinha等 [6] 和Khanjian等 [7] 对矩形通道装有矩形和三角形纵向涡产生器对流体流动和传热特性进行了数值研究。结果表明，由于涡产生器产生强烈的二次流动，破坏了热边界层，加剧了通道壁面附近和中心之间的流体混合并导致传热的增强，且压力损失相对较小。Habibi等 [8] 对由三个弯曲管道组成的扭曲管中的层流传热进行了数值模拟。讨论了雷诺数和管壁温度变化对二次流动拓扑结构的影响，以及它们与传热强化的一致性。Wu等 [9] 采用实验的方法对换热管内流体流动与传热进行了可视化研究，分析了管内流体的二次流特性。研究结果表明，管内流体的二次流与其传热机理有着密切的关系。Lin等 [10] 对传统扭带结构进行改进，按特定形状切除部分扭带基体形成一种传统涡产生器内插件，在均匀壁温条件下，采用数值方法对内插圆管的平行四边形涡产生器管内层流流动和传热特性进行研究。武永和等 [11] 对内插不同形状传统涡产生器管内层流流动与传热特性进行数值研究。研究发现，内插不同形状的涡产生器后，管内二次流强度Se和平均Nu数均随Re的增大而增大，二者的变化具有一致性。

以上文献验证了管内二次流强度和努塞尔数有相同的变化趋势，通过研究二次流的影响因素，可以进一步研究管内换热。本文基于这一研究基础，采用数值模拟的方法，对内置不同形状的涡产生器管内流体流动特性进行研究，分析涡产生器形状对管内二次流强度和阻力系数的影响。

2. 物理模型与数学模型

2.1. 物理模型

如图1(a)所示，扭曲涡产生器具有周期性结构，是在传统扭带的基础上，按照既定几何形状裁去部分材料的薄金属片沿轴向螺旋扭转而成。未经扭曲的薄金属片(本文称为基片)，其结构简图如图1(b)所示。

Figure 1. Schematic diagram of twisted vortex generator

图1. 涡产生器结构示意图

涡产生器厚度为δ，其扭转180度的轴向长度为节距H，基片宽度为W，T_r为扭率(或扭曲比)，扭率的大小对圆管内二次流的强度起决定性作用，其定义式为：

$T_{\text{r}}=H/W$ (1)

定义扭带的螺旋角α为涡产生器的攻击角，与扭带扭率T_r有以下关系：

$\alpha =\arctan \left[\pi /\left(2H/W\right)\right]$ (2)

基片形式下涡产生器的结构参数定义为：W_b为无涡产生器部分的基片宽度，称为基带宽度；W为有涡产生器部分的基片宽度；β和γ为涡产生器的迎流形状角和背流形状角；B为每个涡产生器与管壁接触的轴向长度；S_s是未扭曲之前相邻涡产生器之间的间距；S_t是扭曲后相邻涡产生器之间的间距，其大小由涡产生器攻击角α和未扭曲之前相邻涡产生器之间的间距S_s决定，具体关系式为：

(3)

由于涡产生器形状及结构参数较多，本文仅对内置不同形状的涡产生器的管内层流流动进行了数值模拟，值得注意的是不同形状的涡产生器在扭带上裁去部分的面积相等，其结构参数如表1所示，涡产生器形状为等腰梯形(TVG1)、平行四边形(TVG2)、直角梯形(TVG3)和矩形(TVG4)，固定涡产生器的攻击角α (即扭率T_r)、涡产生器的间距S_t和基带宽度W，通过改变涡产生器与管壁接触的轴向长度B以保证扭带上裁去部分的面积相等。

为了节约计算资源，对计算域进行简化，选取一段包含8对涡产生器的流动管道作为计算域模型，其结构简图如图2所示。加长入口段长度使流体流动达到充分发展，延长出口段以消除出口干扰的影响，入口段出口段的长度L₁、L₃均为10D。本文所研究雷诺数范围选取Re = 50~800。

Table 1. Geometrical parameters of vortex generator

表1. 涡产生器结构参数

Figure 2. Computational domain

图2. 计算域模型

2.2. 物理模型建立过程

本文利用SolidWorks软件对内置涡产生器的圆管建立物理模型。采用“先内后外”的建模思路，首先建立涡产生器及其基带部分的模型，然后建立换热管模型，具体方法为：1) 在SolidWorks中建立直径为W的圆柱模型；2) 在圆柱模型上按照一定形状采用旋转切除命令切除掉多余部分的模型，得到未切除之前的原始模型；3) 在原始模型的基础上通过扫描切除命令得到涡产生器及基带模型，如图3(a)所示；4) 进行仿真模拟时，简化管壁，认为壁面上没有厚度。通过拉伸命令得到圆管内置涡产生器模型，如图3(b)所示。

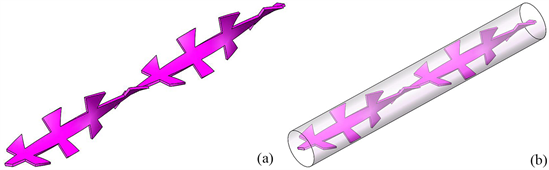
Figure 3. Model diagram established by SolidWorks

图3. SolidWorks建立的模型图

2.3. 数学模型

为建立流体流动的数学模型，作以下简化假设：1) 流体和涡产生器的物性参数为常数；2) 内插涡产生器圆管内流动是定常不可压缩流动；3) 不考虑流体中的粘性耗散和质量力。

在作上述假设后，计算区域的控制方程如下：

连续性方程：

$\frac{\partial u_i}{\partial x_i}=0$ (4)

动量方程：

$\frac{\partial }{\partial x_i}\left(\rho u_i{u}_k\right)=\frac{\partial }{\partial x_i}\left(\mu \frac{\partial u_k}{\partial x_i}\right)-\frac{\partial p}{\partial x_k},\left(k=1,2,3\right)$ (5)

边界条件：

在x-y-z直角坐标系中，边界条件的数学表达式如下：

进口(Inlet)处：通过UDF施加充分发展的入口速度，其公式如(6)所示：

$u_{\text{in}}=u_{\text{c}}\left(1-\frac{r^2}{R^2}\right),v=w=0$ (6)

式中，u_c是圆管中心的速度。

出口(Outlet)处：

$\frac{\partial u}{\partial x}=\frac{\partial v}{\partial x}=\frac{\partial w}{\partial x}=0$ (7)

在测试段圆管壁上，速度为无滑移边界条件：

$u\left(x,y,z\right)=v\left(x,y,z\right)=w\left(x,y,z\right)=0$ (8)

入口段和出口段圆管壁上，速度为无滑移边界条件。

在与基带和涡产生器接触面上，速度为无滑移边界条件：

$u\left(x,y,z\right)=v\left(x,y,z\right)=w\left(x,y,z\right)=0$ (9)

参数定义：

雷诺数Re和阻力系数f定义为：

$Re=\frac{\rho u_{\text{m}}D}{\mu },f=\frac{2\Delta pD}{\rho u_{\text{m}}^2{L}_2}$ (10)

式中，L₂是计算域中测试段圆管的长度，Δp是测试段的压降，u_m是光滑圆管进口截面的平均速度。

流动阻力系数计算公式为：

$f_0=64/Re$ (11)

绝对涡通量的定义式为 [12] [13]：

$J_{\text{ABS}}^n={\displaystyle \iint \left|{\omega }^n\right|\text{d}A/A}$ (12)

$J_{\text{ABS}}^n={\displaystyle \iint \left|{\omega }^n\right|\text{d}V/V}$ (13)

式(12)为截面上的绝对涡通量，式(13)为计算区域流体的绝对涡通量。

二次流强度的定义式为：

$Se=\rho J_{\text{ABS}}^{\text{n}}{D}_h^2/\mu$ (14)

2.4. 网格划分

本文利用ANSYS ICEM软件对圆管内置涡产生器模型进行网格划分。采用“先面后体”的划分网格思路，首先在进口或出口面上的划分面网格，然后由面网格拉伸成体网格，具体方法为：1) 模型导入ANSYS ICEM软件之后，对模型进行拓扑处理，检查模型是否完整；2) 对模型进口进行面网格划分，得到圆柱面上的面网格。3) 将已经划分好的面网格沿着引导线进行旋转拉伸，得到内置涡产生器管内结构块的分布。4) 将得到的结构化块的点线面与建立的模型的点线面进行关联，得到的初步网格示意图。5) 细化网格。调整网格节点数量，生成高网格质量的网格。为了清楚表示圆管壁面处与涡产生器处的网格分布，本文截取两组涡进行展示，如图4所示。

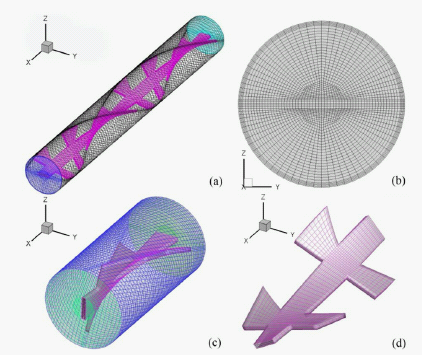
Figure 4. Schematic diagram of grid division by ICEM

图4. ICEM划分的网格示意图

3. 网格独立性考核及算法考核

3.1. 网格独立性考核

对Re = 400时圆管内插扭曲涡产生器(T_r = 4, S_t/W = 0.989, B/W = 0.578, W_b/W = 0.3, β = γ = 60˚)管内流体层流流动的数值模拟结果进行了网格考核，不同网格数下的计算结果如表2所示。经考核，在计算层流状态时圆管内插扭曲涡产生器管内流体流动特性时采用的网格为网格3。

Table 2. Grid independence test

表2. 网格独立性考核

3.2. 数值结果准确性验证

本文对光滑圆管管内层流流动进行了数值模拟，并将模拟结果与公式(11)的计算结果进行了对比验证，对比结果如图5所示。通过对比，说明本文所采用的数值模拟方法是可靠的。

4. 数值结果分析

4.1. 涡产生器形状对平均阻力系数与二次流强度的影响

如图6所示，内插不同形状涡产生器的管内二次流强度与阻力系数随雷诺数的变化。如图6(a)所示，随着雷诺数Re增加，内插不同形状涡产生器管内流体的阻力系数f逐渐变小。Re = 50~800范围内，涡产生器形状对管内流体的阻力系数f影响很小。如图6(b)所示，随着雷诺数Re增加，内插不同形状涡产生器管内流体的二次流强度Se逐渐变大。Re = 50~200范围内，不同形状涡产生器的二次流强度基本相同；Re = 200~800范围内，不同形状涡产生器的二次流强度发生变化，等腰梯形涡产生器的二次流强度逐渐高出其他三种形状，但都呈现增大的变化趋势。

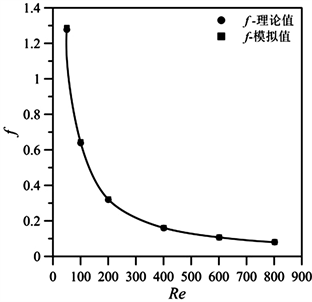
Figure 5. Comparison of Nu_m and f between simulation results and empirical formulas

图5. Nu_m和f模拟结果与经验公式的比较

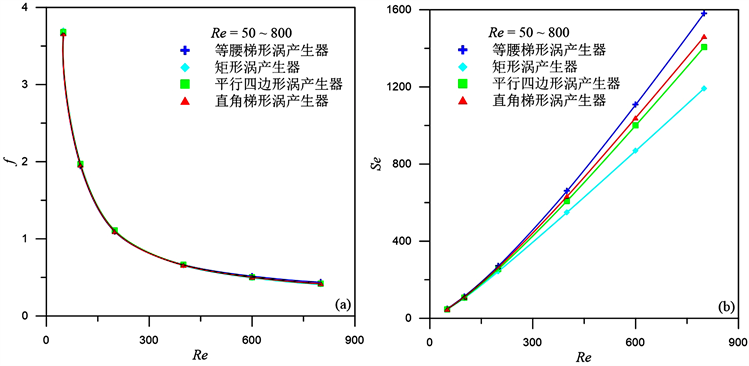
Figure 6. The variation of average resistance coefficient and secondary flow intensity with Reynolds number Re

图6. 平均阻力系数与二次流强度随雷诺数Re的变化

图7为Re = 400时，管内置不同形状的涡产生器后流体的流线图。如图所示，流体通过入口段的光滑圆管内，流体流线是一簇平直的线条，在流经测试段时，由于扭曲的基带和涡产生器的限制和影响，流体沿着基带和涡产生器之间的空间做螺旋运动。涡产生器形状的不同导致流体的混合程度不同，流线形状也不相同。流体流经出口段后，受扭带和涡产生器影响，流体仍做螺旋运动，随着出口段的延长，流体又恢复到入口时的运动状态。

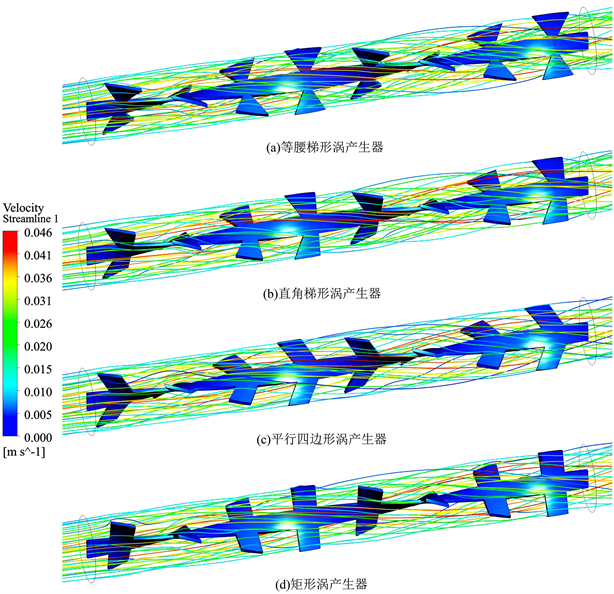
Figure 7. When Re = 400, the fluid flow diagram after inserting vortex generators of different shapes into the tube

图7. Re = 400时，管内插不同形状涡产生器后流体流线图

为了具体分析涡产生器对流体流动的影响，下面将对内置不同形状涡产生器的管内流体流动的局部阻力系数和二次流强度进行分析。

4.2. 涡产生器形状对局部阻力系数和二次流强度的影响

图8为Re = 400，x = 0.19~0.334m范围内，内置不同形状涡产生器对管内流体流动方向上局部阻力系数和二次流强度的影响。由于涡产生器排布的周期性，沿流体流动方向的局部阻力系数和二次流强度呈现出周期性变化。图8(a)为内置不同形状涡产生器管内流体的局部阻力系数随流体流动的变化曲线。内置不同形状涡产生器的管内流体的局部阻力系数在流动方向上呈现周期性下降的变化趋势，而涡产生器的形状对管内流体沿流动方向的局部阻力系数影响较小。图8(b)为内置不同形状涡产生器诱导管内流体产生的二次流在流体流动方向上的变化趋势。不同形状的涡产生器诱导管内流体产生的二次流呈现周期性上升趋势，这说明管内流体产生的涡会随着流体流动向后传递。在x = 0.19~0.334m范围内，等腰梯形涡产生器诱导产生二次流最强，直角梯形涡产生器次之，矩形涡产生器诱导产生的二次流最弱。

为了更好地研究每一个涡产生器对管内流体流动的影响，选取5号涡作为研究对象进行分析。如图9所示为沿流体流动方向上涡产生器的编号及5号涡不同位置的截面分布。

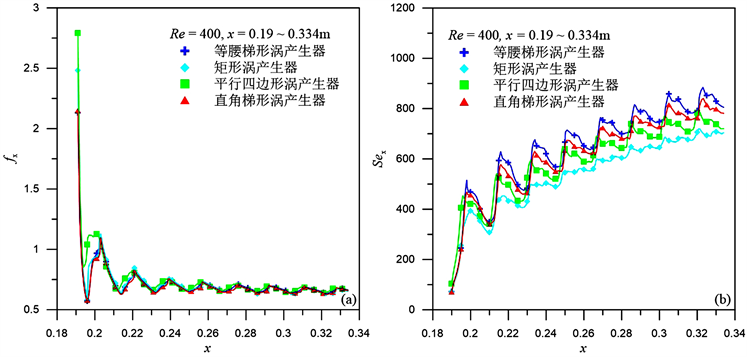
Figure 8. When Re = 400, the influence of vortex generators of different shapes on the local resistance coefficient and the local secondary flow strength

图8. Re = 400时，涡产生器形状对局部阻力系数和二次流强度的影响

Figure 9. Section position

图9. 截面位置图

图10所示为Re = 400时，内置等腰梯形涡产生器管内流体沿流动方向上截面的流线图。在x = 0.261 m的截面上，基带诱导流体旋转流动；随着流体沿主流方向不断流动，流体流进布置有涡产生器的区域，涡产生器和基带区域的流体出现小的漩涡，此时漩涡靠近管壁位置且处于基带两侧，如图10(c)所示；当流体流进涡产生器中间区域时，基带两侧的漩涡开始向管子中心位置移动，如图10(d)所示；在之后的流体流动区域，流体又恢复到流体进入涡产生器区域之前的流动。这说明涡产生器可以改变局部流体区域的流动，使得流体能够产生更加强烈的旋转流动。

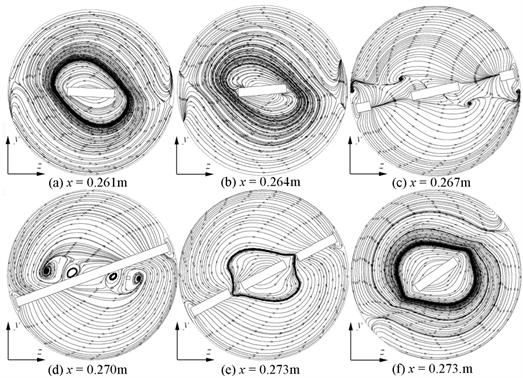
Figure 10. Flow diagram at different positions in the tube

图10. 管内不同位置流线图

图11所示为Re = 400，x = 0.270 m时，内置不同形状涡产生器管内流体流动的流线图。在x = 0.270 m处，内置不同形状涡产生器后，圆管内流体在涡产生器区域的流线分布发生变化。与矩形涡产生器和平行四边形涡产生器相比，内置等腰梯形涡产生器和直角梯形涡产生器的管内流体在涡产生器区域都产生了小的漩涡，并且漩涡分布于涡产生器的两侧。这说明不同形状的涡产生器可以改变管内流体的流动状态，使管内局部流体再次发生旋转。

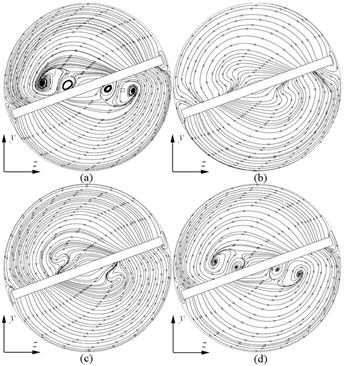
Figure 11. When x = 0.270 m, flow diagram of the fluid inside the vortex generator with different shapes. (a) Isosceles trapezoidal vortex generator; (b) Rectangular vortex generator; (c) Parallelogram vortex generator; (d) Right-angle trapezoidal vortex generator

图11. x = 0.270 m，内置不同形状涡产生器管内流体的流线图。(a) 等腰梯形涡产生器；(b) 矩形涡产生器；(c) 平行四边形涡产生器；(d) 直角梯形涡产生器

图12所示为Re = 400时，5号涡的不同位置二次流强度云图。如图所示，对于同一种形状的管内流体流动，在仅有基带的位置，二次流主要分布在管壁处；在基带和涡产生器组合处，管壁的二次流逐渐增强，且基带和涡产生器也产生了二次流。结合图10不同位置的流线图，发现流线发生变化时，二次流强度也发生变化。涡产生器诱导流体在涡产生器两侧产生小的漩涡，导致二次流增强。这说明涡产生器可以诱导产生较强的二次流。

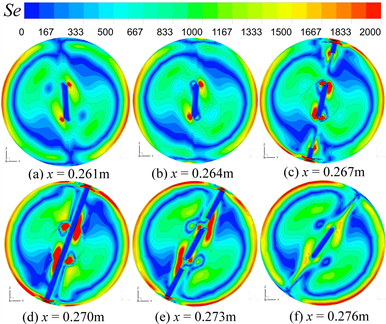
Figure 12. Cloud map of secondary flow distribution at different positions in the tube

图12. 管内不同位置二次流分布云图

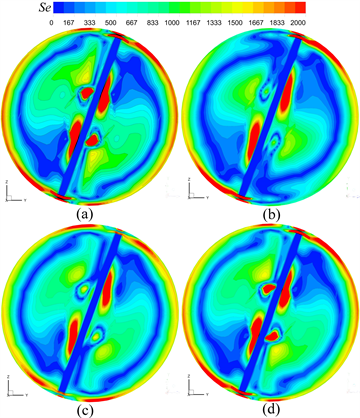
Figure 13. When x = 0.270 m, cloud map of secondary flow distribution of vortex generators of different shapes. (a) Isosceles trapezoidal vortex generators; (b) Rectangular vortex generator; (c) Parallelogram vortex generator; (d) Right-angle trapezoidal vortex generator

图13. x = 0.270 m，不同形状涡产生器二次流分布云图。(a) 等腰梯形涡产生器；(b) 矩形涡产生器；(c) 平行四边形涡产生器；(d) 直角梯形涡产生器

当x = 0.270 m时，不同形状涡产生器导致管内二次流强度分布如图13所示。在管壁处，矩形涡产生器诱导的二次流主要靠近涡产生器处，其他三种形状的涡产生器诱导的二次流存在于管壁各个位置；在基带部分，等腰梯形涡产生器和直角梯形涡产生器诱导的二次流在基带两侧都存在，而矩形涡产生器和平行四边形涡产生器诱导的二次流只存在于基带一侧。

5. 结论

本文对内置不同形状的扭曲涡产生器的圆管管内层流流动进行了数值模拟，分析了涡产生器形状对管内层流流动特性的影响。得到的主要结论如下：

1) 在Re = 200~800范围内，在扭带裁去部分面积相同的情况下，等腰梯形涡产生器诱导产生的二次流最强，直角梯形涡产生器次之，矩形涡产生器最差；涡产生器的形状对管内流体的平均阻力系数影响较小。

2) 涡产生器的形状对管内流体沿流动方向的局部阻力系数影响较小；管内诱导产生的局部二次流大小依次为：等腰梯形涡产生器 > 直角梯形涡产生器 > 平行四边形涡产生器 > 矩形涡产生器。

由于管壁和涡产生器共同作用，靠近管壁的流体会产生更强的二次流；沿着流体流动方向，涡产生器区域的二次流强于基带区域；涡产生器可以诱导产生漩涡。

基金项目

感谢甘肃省高等学校科研成果转化项目(2018D-12)的资助。

NOTES

^*通讯作者。