多排凹坑对叶片气动及噪声特性的研究

Study on Aerodynamic and Noise Characteristics of Blades with Multiple Rows of Pits

摘要: 本文通过改变叶片两种凹坑的排列方式，采用大涡模拟(LES)方法探究相对长度和排列方式对叶片的气动特性的影响，声场上采用LMS Virtual.lab直接边界元法研究了相对长度和排列方式对叶片的噪声特性的影响，并揭示了多排凹坑设计对叶片边界层流动控制及噪声抑制的机理。研究结果表明：排布方式对卵圆形凹坑的影响不大，采用矩形排布的圆形凹坑时叶片尾缘压力脉动明显下降。多排凹坑引起高频段窄带噪声增大，其中圆形凹坑模型的总声压级下降约3 dB。当采用菱形排布时降噪效果更好，此时额外诱导的周期性涡脱落噪声较小。通过进一步研究分析，认为多排凹坑降噪的机理为：吸力面表面凹坑设计对叶片湍流流动具有一定的控制效果，坑面处形成的反向涡流干扰了边界层内相干结构的展向联系，一定程度上可以抑制尾缘处大尺度脱落涡形成，削弱壁面分离流结构，可以有效降低与大尺度相干涡关联的中低频噪声。

Abstract: In this paper, by changing the arrangement of the two pits of the blade, the large eddy simulation (LES) method was used to investigate the influence of relative length and arrangement on the aerodynamic characteristics of blades. The effects of relative length and pit arrangement on blade noise characteristics were studied by LMS Virtual.lab direct boundary element method, and the mechanism of multi-row pit design on flow control and noise suppression of blade boundary layer were revealed. The research results show that: the arrangement has little effect on oval pits blades, the pressure pulsation at the trailing edge of the blade decreases obviously when the circular pit is arranged in a rectangular pattern. Multiple rows of pits cause high frequency narrow-band noise to increase, and the total sound pressure level of the circular pit model decreased by about 3 dB. The noise reduction effect is better when diamond layout is adopted. At this time, the additional induced periodic vortex shedding noise is smaller. Through further research and analysis, it is concluded that the noise reduction mechanism of multi-row pits is that: the design of the pit on the suction surface can control the turbulent flow of the blade; the backward eddy currents formed at the pit surface interfere with the spanwise relations of the coherent structures in the boundary layer; to some extent the formation of large scale shedding vortex at trailing edge can be restrained, and wall separation flow structure is weakened, that can effectively reduce the low and medium-frequency noise associated with large scale vortices.

1. 引言

2015年，国家标准委员会针对风力机组对居民产生一种“风电场综合征”的影响，引起了人们耳鸣、眩晕症状，诱发失眠症、心脏病等疾病的问题，修订并施行相关标准《风力发电机组噪声测量方法》，保证居民的健康生活 [1]。风机的气动噪声包括旋转噪声与湍流噪声，旋转噪声是一种离散性噪声，容易观测与感知，湍流噪声属于宽频性噪声，在低速低压工况中占主导作用，是降噪的主要目标。目前，降低湍流噪声的方法有锯齿尾缘、多孔表面、以及非光滑表面等。对于非光滑表面方法，Walsh等 [2] 在上世纪末打破传统思维方式，证明了流向沟槽表面可以有效降低平板表面摩擦阻力。经过系统性试验研究后 [3] [4] [5] [6]，学者发现形状、尺度、布置方式合适的小肋沟槽具有较好的湍流减阻效应。国外学者发现 [7] [8] [9]，具有酒窝表面的高尔夫球可以飞得更远，说明酒窝凹坑具有减阻能力。受沙漠中自然地形的启发，周培 [10] 研究了一种卵圆形凹坑，发现其具备比圆形凹坑更好的压力连带效应，凹坑面沿流动方向上形成了高速–低速–高速的速度分布带，低速区与高速区之间的压降抵消了部分压差阻力。李凯杰 [11] 将深径比为0.5的凹坑阵列应用在离心泵叶轮吸力面上，发现凹坑内部的低速反向小涡结构减少了壁面受力，使模型的扬程和效率提升。杨弘炜 [12] 等采集中华鲟皮肤特征，设计了菱形排布的凹坑点阵织构并应用于NACA16012翼型上，经水洞试验后，翼型阻力系数下降22%。叶轮机械的介质通常处于高温高压状态，需要考虑叶片壁面的磨损、腐蚀，因此实际应用中需要考虑非光滑表面结构强度。多排凹坑具有设计简单、结构稳定、对非光滑表面结构强度要求较低的特点，目前关于吸力面凹坑排列方式对叶片自噪声影响的研究较少，故有必要进一步展开研究。

2. 数值计算方法

2.1. 几何模型及边界条件

本文以NACA6510片为基础叶片，弦长C = 100 mm，展长B = 15 mm，图1为非光滑叶片吸力面上多排凹坑结构的俯视图，非光滑面上排布了相同尺寸的凹坑元素，如虚线区域显示。根据刘家成等 [13] 分析结论，选取深径比为0.2的卵圆形凹坑，从0.65C处开始排布。非光滑面的相对长度L/C分别取5%、7.5%、12.5%，排布方式采用矩形排布与菱形排布，得到6组参数的E系列非光滑面，以分析各参数模型下湍流边界层流动情况。在展开对壁面压力脉动与噪声特性影响的定量分析时，引入相同参数的D系列非光滑面模型，与前6组模型对比。模型主要参数见表1。

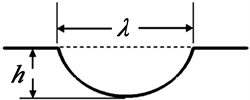(a) 圆形结构 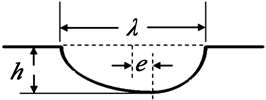(b) 卵圆形结构 (c) 相对长度定义示意图

Figure 1. Two-dimensional diagram of non-smooth surface of suction surface of blade

图1. 叶片吸力面的非光滑面二维示意图

Table 1. Main parameters and values of the model

表1. 模型主要参数及数值

计算域进口和上下远场均给定自由来流速度条件，速度U为30 m/s，雷诺数Re = 2 × 10⁵。出口于叶片下游约30C处，采用自由出流条件，叶片壁面为无滑移条件，叶片展向方向设定为周期性边界条件。

使用商业软件Fluent做叶片流场，声场上采用LMS Virtual.lab直接边界元法。来流工质为空气，基于弦长的雷诺数Re_c = 2 × 10⁵，由于进口马赫数小于0.3，故可认为流动是不可压缩的。定常计算采用SST k-ω双方程湍流模型，将收敛结果作为瞬态计算初始场，开启LES方程同时打开FW-H方程计算叶片绕流流场及辐射声场。给定速度入口，自由出流的边界条件，叶片展向为周期性边界条件，时间步长∆t取2 × 10⁻⁵ s。

对于非定常流动计算，采用大涡模拟可以较好地模拟湍流结构，其原理是：对于受边界条件影响明显的大尺度运动进行直接数值模拟；对于具有较多普适性的小尺度湍流结构则通过构造亚格子模型进行模化。比起对所有小尺度涡采取直接模拟计算，采用大涡模拟时所需计算量要小得多。本文主要分析流动与气动噪声的联系，要求对流场模拟的精度较高、准确较严。有研究表明 [14]，LES方法已具备气动噪声计算的精度需要。

LES方法中，对于变量 $\bar{\varphi }$，空间滤波后变为：

$\bar{\varphi }={\displaystyle {\int }_D\varphi G\left(x,x^{\prime }\right)\text{d}{x}^{\prime }}$ (1)

式中：D为流动区域； $G\left(x,x^{\prime }\right)$ 为滤波函数，其表达式如下：

$G\left(x,x^{\prime }\right)=\{\begin{array}{l}1/V,x^{\prime }\in V\\ 0,x^{\prime }\notin V\end{array}$ (2)

式中：V为计算网格单元的体积。将式(2)代入式(1)可得：

$\bar{\varphi }=\frac{1}{V}{\displaystyle \underset{D}{\int }\varphi \text{d}{x}^{\prime }}$ (3)

用式(3)处理连续性方程及瞬时N-S方程，可得：

$\frac{\partial \overline{u_i}}{\partial x_i}=0$ (4)

$\rho \frac{\partial \overline{u_i}}{\partial t}+\rho \frac{\partial }{\partial x_j}\left(\overline{u_i}\overline{u_j}\right)=-\frac{\partial \bar{p}}{\partial x_i}+\frac{\partial y}{\partial x_i}\left(\mu \frac{\partial \overline{u_i}}{\partial x_j}\right)-\frac{\partial {\tau }_{ij}}{\partial x_j}$ (5)

式(4)和(5)即为不可压缩大涡模拟运动方程，式中滤波后的变量带有上划线，其中，方程以 ${\tau }_{ij}=\rho \overline{u_i{u}_j}-\rho \overline{u_i}\overline{u_j}$ 亚格子应力表征小尺度涡对大涡运动方程的影响。本文采用动力Smagorinsky-Lilly亚格子动力模型：

${\tau }_{ij}=-2{\mu }_t\overline{S_{ij}}$ (6)

${\mu }_t={\left(C_s\Delta \right)}^2\left|\bar{S}\right|$ (7)

$\overline{S_{ij}}=\frac{1}{2}\left(\frac{\partial \overline{u_i}}{\partial x_j}+\frac{\partial \overline{u_j}}{\partial x_i}\right)$ (8)

$\left|\bar{S}\right|=\sqrt{2\overline{S_{ij}}\overline{S_{ij}}}$ (9)

上式中， ${\mu }_t$ 为亚格子湍流粘性系数； $\Delta$ 为网格尺度； $C_s$ 为亚格子常数； $\overline{S_{ij}}$ 为网格平均应变率。

2.2. 网格划分及网格无关性验证

网格是离散化的基础。本文利用ICEM对模型进行网格划分。采用三维结构化网格，为了节约工作量，按图2所示划分计算域：其中，A域为外流场，长50C、宽40C，翼型前缘点距离进口及上下边界20C，保证远场条件。计算域高度为叶片翼展b。B域为近流场，距离进口20C，网格需要加密，长3.5C、宽2C、尾迹1.5C，采用外H内O型拓扑结构，A、B两子域交界面的流向方向网格一一对应。叶片表面Y⁺值均小于1，满足大涡模拟对计算网格的要求。

本文对吸力面多排凹坑的叶片模型设置了4套方案，在6˚攻角下进行网格无关性验证。由表2可见，当网格量超过520万时，计算结果已基本保持稳定，升阻比变化率不超过0.02%。故采用第4种网格方案，整体网格量控制在520万到550万之间。

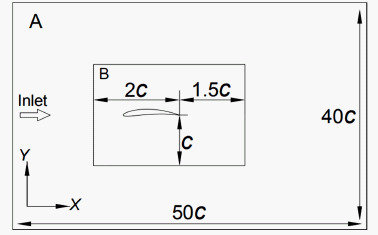
Figure 2. Schematic diagram of numerical calculation domain

图2. 数值计算域示意图

Table 2. Grid independence verification

表2. 网格无关性验证

3. 计算结果分析

3.1. 相对长度、排列方式对叶片气动特性的影响

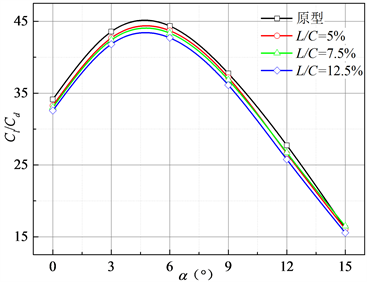
图3为两种排布方式时，不同相对长度的E系列模型叶片气动特性分布。从图中可以看出：① 小攻角下，随着相对长度L/C增大，模型叶片的升阻比逐渐下降，其中α = 0˚时下降较大，L/C = 12.5%时模型的升阻比最差，比原型低4.6%；② 大攻角下，叶片气动性能变化幅度低于小攻角时下降程度，当L/C = 7.5%时，矩形排布模型的升阻比最优，与光滑叶片相比增大1.7%，而菱形时增大0.9%。

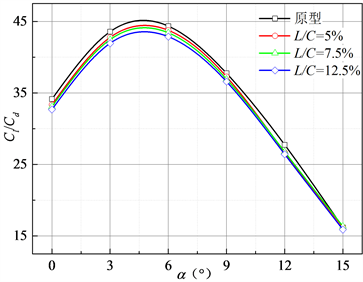(a) 矩形排布 (b) 菱形排布

Figure 3. Influence of relative length on aerodynamic characteristics of E series models

图3. 相对长度对E系列模型气动特性的影响

当不改变凹坑的流向长度λ、正交深度h时，凹坑多排设计会增大其压差阻力，故小攻角下叶片升阻比明显下降。综上所述，在本文关注的参数范围内卵圆形凹坑排布不能有效改善叶片整体气动特性，因此，本文将重点分析多排凹坑设计对叶片绕流流场非定常特性及噪声特性的影响。

3.2. 相对长度、排列方式对叶片尾缘涡核心区的影响

光滑叶片的表面流动经历了转捩过程，壁面出现湍流流动，尾缘流动发生分离，并随着攻角增大壁湍流逐渐发展充分，分离流范围扩大，产生大面积分离。非光滑表面具有多个内陷的反向涡对，可视为组合式的涡流发生器，通过壁面分布的二次涡流结构，影响壁湍流中二维性流向涡的生长尺度。因此，有必要对非光滑叶片的涡核心区进行分析，以分析多排凹坑设计对附面层涡系运动的影响。

图4为α = 0˚时光滑叶片涡核心区分布云图，图5为α = 0˚时E系列非光滑叶片涡核心区分布云图，各云图已用速度大小渲染。横向对比可以看出，随着非光滑面相对长度增大，附面层管状涡的尺度明显减少。这说明非光滑壁面对附面层流向涡的生长具有显著抑制作用，凹坑内部的反向涡对很好地抑制了Λ涡区的发生位置，大尺寸流向涡的展向联系被坑面的反向涡流削弱。纵向对比来看，矩形排布模型的表面涡流成核发生概率下降，相对长度较大时矩形排布对流向涡抑制更强。

Figure 4. Q criterion vortex-nucleus isosurface of a smooth blade (α = 0˚)

图4. α = 0˚时光滑叶片Q准则涡核等值面

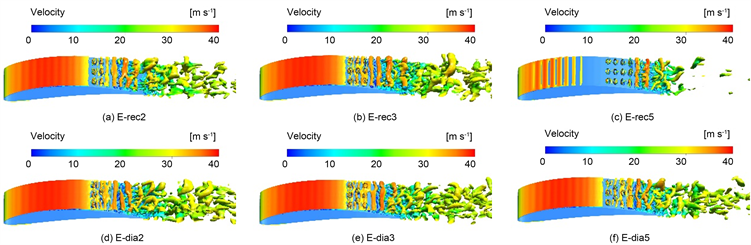
Figure 5. The E series non-smooth blade Q criterion vortex core isosurface (α = 0˚)

图5. α = 0˚时E系列非光滑叶片Q准则涡核等值面

3.3. 相对长度、排列方式对叶片压力脉动的影响

根据上文分析，凹坑内部反向涡对抬升，其展向分布理论上可以影响湍流边界层内的相关结构，削弱大尺度流向涡，有助于降低壁面压力脉动程度。R D Sandberg等 [15] 对低雷诺数下NACA0012翼型绕流流场进行分析，研究分析发现，当转捩发生时尾缘噪声要远比未发生时的强烈，这侧面说明转捩发生时叶片尾缘的脉动激励声源强烈。对L/C = 7.5%时E系列非光滑模型进行分析，同时与同参数D系列模型比较。如图6所示以尾缘2 mm处监测点g为分析对象，图7、图8分别为0˚、12˚攻角下不同模型尾缘处压力脉动对比。

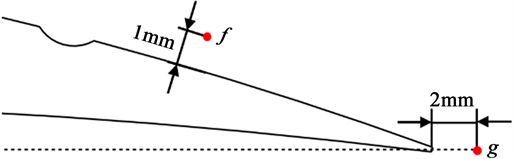
Figure 6. Schematic diagram of monitoring point location distribution

图6. 监测点位置分布示意图

图7可以看出，α = 0˚时各模型可以大幅度降低压力脉动主峰幅值，最大幅值下降了100 Pa，降幅80%，各模型压力脉动幅值主要在中低频。其中E系列非光滑面在两种排布下压力脉动幅值最小，而D系列模型则说明矩形排布更有效。

(a) 矩形排布 (b) 菱形排布

Figure 7. Pressure pulsation distribution at trailing edge point g of the blade (L/C = 7.5%, α = 0˚)

图7. L/C = 7.5%时叶片尾缘点g压力脉动分布(α = 0˚)

图8可以看出，α = 12˚时各模型降低了叶片尾缘压力脉动最大幅值，最大峰值频率从33 Hz变化为150 Hz，其中矩形排布相对较优，D系列模型降低幅值约71%，E系列模型降低约59%。综合两张图来看：(1) 排布方式对卵圆形凹坑的影响不大；(2) 矩形排布的圆形凹坑使压力脉动进一步降低。整体来看，0˚及12˚攻角下非光滑面对尾缘压力脉动均有一定抑制效果，0˚时卵圆形凹坑设计显著抑制了尾缘压力脉动，α = 12˚时圆形凹坑设计效果更好，这侧面反映了卵圆形凹坑内部涡流大，对下游流动的调控效果较明显。

3.4. 相对长度、排列方式对叶片远场噪声的影响

总体来看，排布方式对多排凹坑设计的噪声抑制具有重要影响，因此，本文在各个攻角下对相对长度L/C = 7.5%时不同模型噪声特性进行对比分析。

(a) 矩形排布 (b) 菱形排布

Figure 8. Pressure pulsation distribution at trailing edge point g of the blade (L/C = 7.5%, α = 12˚)

图8. L/C = 7.5%时叶片尾缘点g压力脉动分布(α = 12˚)

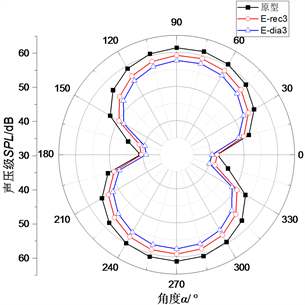
图9为α = 0˚时各模型叶片噪声辐射指向性。图中反映，各非光滑模型叶片的总声压级各方向上均下降。其中尾缘方向330˚下降约5.4 dB，下降较为明显。D系列模型的降噪效果整体较好，相对长度为7.5%时总声压级低了14%。

(a) E系列非光滑面 (b) D系列非光滑面

Figure 9. The directional distribution of noise radiation from the model blades (α = 0˚)

图9. α = 0˚时模型叶片噪声辐射指向性分布

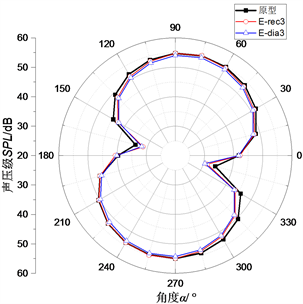
图10为α = 6˚时不同排布方式的模型叶片的噪声指向性。图中可见，非光滑叶片的总声压级与光滑叶片相当，此时排布方式变化对总声压级几乎没影响，这说明6˚攻角下，对相对长度L/C = 7.5%时不同模型而言，多排设计的凹坑在展向上对湍流边界层的影响变弱。

为更好的探究噪声降低的频谱特性，选择如图11处的监测点7，分析了0˚、6˚攻角下该点处的频谱特性。图12为0˚攻角下，各模型于监测点7处的无计权噪声频谱图。图中可见，各模型的中低频噪声有所下降，其中菱形排布的圆形凹坑模型在1150 Hz下声压级最低，下降约27 dB，幅值下降46%。图13为6˚攻角下，各模型于监测点7处的无计权噪声频谱图。图中可见，各模型在1 kHz内低频噪声下降更明显，但是6 kHz附近出现窄带离散噪声，从图可以看出，采用矩形排布时，高频离散噪声的峰值特征更明显。

(a) E系列非光滑面 (b) D系列非光滑面

Figure 10. The directional distribution of noise radiation from the model blades (α = 6˚)

图10. α = 6˚时模型叶片噪声辐射指向性分布

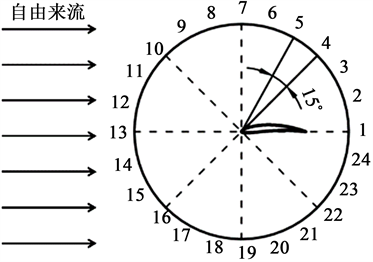
Figure 11. Diagram of acoustic monitoring points

图11. 声学监测点示意图

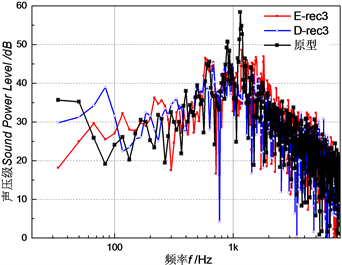(a) 矩形排布 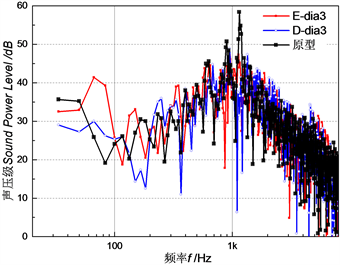(b) 菱形排布

Figure 12. Spectrum diagram of sound pressure level at the model blade receiving point Recei-7 (α = 0˚)

图12. α= 0˚时模型叶片接收点receive-7处声压级频谱图

(a) 矩形排布 (b) 菱形排布

Figure 13. Spectrum diagram of sound pressure level at the model blade receiving point Recei-7 (α = 6˚)

图13. α= 6˚时模型叶片接收点receive-7处声压级频谱图

4. 结论

通过流场数值模拟计算和声比拟混合方法，研究了不同攻角下两种类型非光滑表面的相对长度与排布方式对气动特性、绕流流场特性及噪声特性的影响，通过分析获得以下结论：

1) 小攻角下，多排凹坑的非光滑面显著增大了叶片阻力系数，故升阻比下降较为明显，当相对长度L/C = 12.5%时，升阻比下降4.6%；大攻角下，叶片阻力系数下降不明显，总体上升阻比较原来轻微下降。故当多排凹坑布置在分离区时，非光滑叶片具有较好的气动性能。

2) 从瞬时流动特性来看，多排凹坑对壁面非定常流动具有较强的调节作用。以6˚攻角为例，凹坑内部反向涡对调节底层紊流动能，将低速区抑制在0.7倍弦长以内，增大了下游壁面流动动能，改善了附面层速度亏损，有利于抑制壁面分离、抑制湍流边界层发展。从各模型来看，矩形排布优于菱形排布，相对长度较大时矩形排布的调节效果明显。叶片厚度、弯度增大不仅会使叶片分离点位置前移，还会恶化分离后的边界层内流动，使边界层增厚、层内速度扰动加剧，不稳定流动与叶片间的相互作用增强。

3) 采用声学直接边界元方法分析了叶片噪声特性：① 当α = 0˚时，菱形排布的卵圆形凹坑对流场中大涡破碎更彻底，总声压级下降幅度可达11.2%；② 当α = 12˚时，随着相对长度L/C增大，多排凹坑引起高频段窄带噪声增大，其中圆形凹坑模型的总声压级下降约3 dB。当采用菱形排布时降噪效果更好，此时额外诱导的周期性涡脱落噪声较小。