多种角度探究椭圆的焦半径、焦点弦、∠F1PF2的最大值问题

The Maximum of Focal Radius, Chord of Focus and Angle ∠F1PF2 of Ellipse Are Studied from Different Angles

摘要: 椭圆的焦半径、焦点弦、焦点三角形等相关知识是高考的难点，也是学生最容易混淆的知识点之一，只有在学生掌握相关结论的基础上才能更好地解决相关习题。本文主要运用代数、参数方程等方法以及数形结合的思想探究了焦半径、焦点弦的最值问题及焦点三角形的角∠F1PF2最大值问题，从多个角度分析了相关问题，更有助于培养学生的发散思维能力。

Abstract: The focus radius, focus chord and focus triangle of ellipse are the difficult points in the college en-trance examination. Only on the basis of students’ mastery of the relevant conclusions can they better solve the relevant exercises. In this paper, the maximum of focal radius, the chord of focal point and the maximum of angle of focal triangle are studied by means of algebra, parametric equation and the thought of the combination of number and shape. It is more helpful to cultivate students’ ability of divergent thinking.

1. 椭圆的焦半径问题(椭圆上任意一点到焦点的距离)

例1 椭圆 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ ( $a>b>0$ )的左、右焦点分别为 $F_1,F_2$，椭圆上任意一点 $P\left(x_0,y_0\right)$，求 $\left|P{F}_2\right|$ 的取值范围。

解法一 设 $F_2\left(c,0\right)$，由题意可知， $\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}=1$，即 $y_0^2=b^2-\frac{b^2}{a^2}{x}_0^2$，

$\therefore \left|P{F}_2\right|=\sqrt{{\left(x_0-c\right)}^2+y_0^2}=\sqrt{{\left(a-\frac{c}{a}{x}_0\right)}^2}=\left|a-e{x}_0\right|$。

$\because 0<e<1$， $-a\le x_0\le a$， $\left|P{F}_1\right|+\left|P{F}_2\right|=2a$， $\therefore \{\begin{array}{l}\left|P{F}_2\right|=a-e{x}_0\\ \left|P{F}_1\right|=a+e{x}_0\end{array}$ [1]。

解法二 令 $\{\begin{array}{l}{x}_0=a\cos \theta \\ y_0=b\sin \theta \end{array}$ ( θ 为参数)

$\therefore \left|P{F}_2\right|=\sqrt{{\left(a\cos \theta -c\right)}^2+{\left(b\sin \theta \right)}^2}=\sqrt{{\left(a-c\cos \theta \right)}^2}=a-c\cos \theta$。

即 $\left|P{F}_2\right|=a-ea\cos \theta =a-e{x}_0$。

$\because \left|P{F}_1\right|+\left|P{F}_2\right|=2a$， $\therefore \left|P{F}_1\right|=a+ea\cos \theta =a+e{x}_0$，其中 $-a\le x_0\le a$。

2. 椭圆中焦点弦问题

例2 过椭圆焦点的直线与椭圆 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ ( $a>b>0$ )交于 $A,B$ 两点，求弦 $\left|AB\right|$ 的取值范围。

解法一 设直线l的方程为： $x=my+c$，交点坐标分别为 $A\left(x_1,y_1\right),B\left(x_2,y_2\right)$。

$\{\begin{array}{l}\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\\ x=my+c\end{array}\Rightarrow y^2\left(b^2{m}^2+a^2\right)+2mc{b}^{2}y-b^4=0$.

$\therefore y_1+y_2=\frac{-2mc{b}^2}{b^2{m}^2+a^2}$， $y_1{y}_2=\frac{-b^4}{b^2{m}^2+a^2}$，

$\begin{array}{c}\left|AB\right|=\sqrt{1+m^2}\cdot \sqrt{\frac{4m^2{c}^2{b}^4}{{\left(b^2{m}^2+a^2\right)}^2}+\frac{4b^4}{b^2{m}^2+a^2}}=2a{b}^2\cdot \frac{m^2+1}{b^2{m}^2+a^2}\\ =2a{b}^2\cdot \frac{\left(b^2{m}^2+a^2\right)\frac{1}{b^2}+1-\frac{a^2}{b^2}}{b^2{m}^2+a^2}=2a{b}^2\cdot \left(\frac{1}{b^2}-\frac{\frac{a^2}{b^2}-1}{b^2{m}^2+a^2}\right)\end{array}$.

当 $m=0$ 时， ${\left|AB\right|}_{\min }=\frac{2b^2}{a}$ ；

当 $m\to \infty$ 时，即直线l的斜率 $k=\frac{1}{m}$ 越接近0时，弦 $\left|AB\right|$ 越大 [2]，

$\therefore$ 当直线l的斜率为0时， ${\left|AB\right|}_{\max }=2a$。

解法二 设椭圆的方程为 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$，直线l的参数方程为 $\{\begin{array}{l}x=c+t\cos \theta \\ y=t\sin \theta \end{array}$ (其中t为参)。

代入椭圆方程得 $\frac{{\left(c+t\cos \theta \right)}^2}{a^2}+\frac{t^2{\sin }^2\theta }{b^2}=1$，

即

$t^2\left(a^2{\sin }^2\theta +b^2{\cos }^2\theta \right)+t\cdot 2b^{2}c\cos \theta -b^4=0$,

$t_1+t_2=-\frac{2b^{2}c\cos \theta }{a^2{\sin }^2\theta +b^2{\cos }^2\theta }=-\frac{2b^{2}c\cos \theta }{a^2-c^2{\cos }^2\theta }$,

$t_1\cdot t_2=\frac{-b^4}{a^2{\sin }^2\theta +b^2{\cos }^2\theta }=\frac{-b^4}{a^2-c^2{\cos }^2\theta }$,

$\left|AB\right|=\left|t_1-t_2\right|=\sqrt{{\left(t_1+t_2\right)}^2-4t_1\cdot t_2}=\frac{2a{b}^2}{a^2-c^2{\cos }^2\theta }$.

当 ${\cos }^2\theta =1$ 时， $\left|AB\right|$ 有最大值2a；当 ${\cos }^2\theta =0$ 时， $\left|AB\right|$ 有最小值 $\frac{2b^2}{a}$ [3]。

解法三 设过椭圆右焦点F的直线l与椭圆的交点分别为 $A\left(x_1,y_1\right),B\left(x_2,y_2\right)$，由焦半径公式可知：

$\left|AF\right|=a-e{x}_1$, $\left|BF\right|=a-e{x}_2$, $\left|AB\right|=\left|AF\right|+\left|BF\right|=2a-e\left(x_1+x_2\right)$

由解法一可知： $x_1+x_2=m\left(y_1+y_2\right)+2c$，其中 $y_1+y_2=\frac{-2mc{b}^2}{b^2{m}^2+a^2}$ ；

$\therefore \left|AB\right|=2a-e\left(x_1+x_2\right)=2a-\frac{2a{c}^2}{b^2{m}^2+a^2}$。

当 $m=0$ 时， ${\left|AB\right|}_{\min }=\frac{2b^2}{a}$ ；当m足够大时，即直线斜率为0时， ${\left|AB\right|}_{\max }=2a$。

3. 椭圆上任意一点P与椭圆焦点F₁, F₂构成的角ÐF₁PF₂最大值问题

例3 设椭圆的标准方程为： $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ ( $a>b>0$ )，椭圆上任意一点P与椭圆焦点 $F_1,F_2$ 构成的角为 $\angle F_{1}P{F}_2$ ；当P为椭圆的上顶点时(或下顶点时)， $\angle F_{1}P{F}_2$ 最大。

证法一 设椭圆上任意一点P，焦点坐标分别为 $F_1\left(-c,0\right),F_2\left(c,0\right)$，且 $\left|P{F}_1\right|+\left|P{F}_2\right|=2a$。

$\cos \angle F_{1}P{F}_2=\frac{{\left|P{F}_1\right|}^2+{\left|P{F}_2\right|}^2-4c^2}{2\left|P{F}_1\right|\cdot \left|P{F}_2\right|}=\frac{{\left(\left|P{F}_1\right|+\left|P{F}_2\right|\right)}^2-4c^2}{2\left|P{F}_1\right|\cdot \left|P{F}_2\right|}=\frac{2b^2}{\left|P{F}_1\right|\cdot \left|P{F}_2\right|}-1$,

$\left|P{F}_1\right|\cdot \left|P{F}_2\right|\le {\left(\frac{\left|P{F}_1\right|+\left|P{F}_2\right|}{2}\right)}^2=a^2$，当 $\left|P{F}_1\right|=\left|P{F}_2\right|$ 时，等号成立 $\cos \angle F_{1}P{F}_2\ge \frac{2b^2}{a^2}-1$，

$\therefore$ 当 $\left|P{F}_1\right|=\left|P{F}_2\right|$ 时， $\cos \angle F_{1}P{F}_2$ 有最小值， $\angle F_{1}P{F}_2$ 最大，此时点P为椭圆的上顶点(或下顶点)。

证法二 椭圆的参数方程为 $\{\begin{array}{l}x=a\cos \theta \\ y=b\sin \theta \end{array}$ ( $\theta$ 为参数)，则椭圆上的点为 $p\left(a\cos \theta ,b\sin \theta \right)$ [3]；点P到原点O的距离： $\left|OP\right|=\sqrt{a^2{\cos }^2\theta +b^2{\sin }^2\theta }=\sqrt{b^2+c^2{\cos }^2\theta }$。

当 ${\cos }^2\theta =0$ 时，即 $\theta =\frac{\pi }{2}$ (或 $\frac{3\pi }{2}$ )时， ${\left|OP\right|}_{\min }=b$，此时点P为椭圆的上顶点(或下顶点)。

以原点O为圆心， $\left|O{F}_2\right|=c$ 为半径做圆，如图1，图2，图3所示：

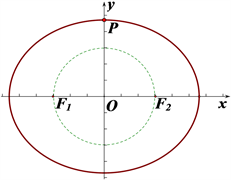
Figure 1. The radius is less than the short half axis

图1. 半径小于短半轴

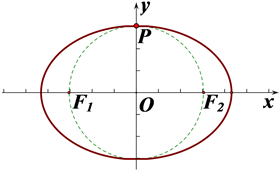
Figure 2. The radius is equal to the short half axis

图2. 半径等于短半轴

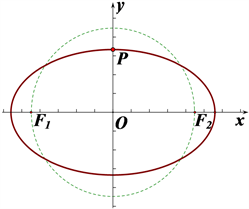
Figure 3. The radius is greater than the short half axis

图3. 半径大于短半轴

$\because$ 点P为椭圆的上顶点(或下顶点时)，到圆心O的距离最短 ${\left|OP\right|}_{\min }=b$

$\therefore$ $\angle F_{1}P{F}_2$ 最大，此时点P为椭圆的上顶点(或下顶点)。

4. 椭圆上任意一点P与椭圆左右顶点A, B构成的角ÐAPB最大值问题

证法一 由于椭圆关于坐标轴对称，不妨设椭圆第一象限上任意一点 $p\left(x_0,y_0\right)$，左右顶点坐标分别为 $A\left(-a,0\right),B\left(a,0\right)$，记 $\angle PAB=\alpha ,\angle PBA=\beta ,\angle APB=\gamma$，如图4所示：

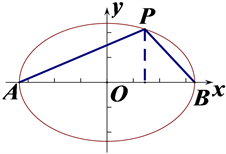
Figure 4. P is the moving point on the ellipse

图4. P为椭圆上动点

$\tan \alpha =\frac{y_0}{x_0+a}$ (1)

$\tan \beta =\frac{y_0}{a-x_0}$ (2)

$\tan \gamma =\tan \left[\pi -\left(\alpha +\beta \right)\right]=-\tan \left(\alpha +\beta \right)=-\frac{\tan \alpha +\tan \beta }{1-\tan \alpha \cdot \tan \beta }$ (3)

将(1)、(2)式带入(3)式整理可得： $\tan \gamma =-\frac{2a{b}^2}{c^2{y}_0}$，当 $y_0=b$ 时， $\tan \gamma =-\frac{2a{b}^2}{c^2{y}_0}$ 最大，即 $\angle APB$ 最大；此时P为椭圆的上顶点。

证法二 以原点为圆心，椭圆长半轴为半径做圆，如图5所示：有上述例3中的证法二可知：椭圆的上顶点到原点的距离最短。因此P为椭圆的上顶点时， $\angle APB$ 最大。

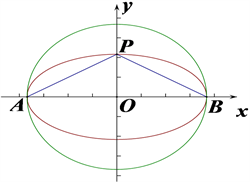
Figure 5. P is the vertex of the ellipse

图5. P为椭圆上顶点

5. 总结

本文在了解椭圆基础知识、参数方程等相关知识的基础上探究了焦半径、焦点弦及焦点三角形中角 $\angle F_{1}P{F}_2$ 的最大值问题；多个角度分析问题，探究相关结论，使得运用结论在解决相关习题时能快速找到突破口。