1. 引言
风工程研究中,常采用主动模拟和被动模拟两类方法来模拟自然环境中风的紊流特性。主动模拟分为振动格栅 [1]、振动尖塔 [2] 和多风扇风洞 [3] 等方法,被动模拟分为被动格栅 [4]、尖劈 [5] 和粗糙元 [6] 等方法。在风洞实验中,一般采用在风洞入口处布置被动格栅的方式来模拟均匀紊流场。张明月 [7] 利用风洞试验的手段研究了测点与格栅间距、格栅板宽度以及单元格栅边长等对风参数的影响规律。文水兵 [8] 通过改变格栅板宽度以及间距的方式,调试出了A、B、C三类地貌的紊流强度。
随着计算机技术的日渐成熟,计算流体动力学(Computational Fluent Dynamics)技术在风工程中的运用越来越多。且较风洞试验而言,数值模拟具有较强的灵活性、流场可观测和成本低等特点,成为了一种验证风洞试验的可靠手段。鲍泽辰等 [9] 将粗糙元、扰流杆以及格栅三者结合,采用LES的方法,模拟了C类地貌的风场特性。杨荣菲等 [10] 通过LES的方法,探讨了格栅稠度、来流风速以及格栅表面粗糙度,对格栅紊流场特性参数的影响。Torrano等 [11] 使用LES方法对被动格栅紊流场进行了数值模拟,并得出结论,y+在30~300之间也可以得到较好的流场特性参数。验证了运用LES紊流模型模拟格栅紊流场的可行性。
理想化的阵风模型可分为TSI阵风模型和IEC阵风模型 [12] 等,但有研究表明将TSI阵风模型运用于桥梁抗风研究存在不足 [13]。IEC阵风模型是国际电工委员会制定的IEC61400-1标准中提出的,其主要特点表现为风速在短时间内减小到最小值,接着又急剧增大达到最大风速值,随后又在极短时间内迅速下降再次变为最小值,最后恢复为阵风发生前的速度。赵元元 [14] 利用流体力学前处理软件Gambit建立起1.0 MW风机的叶片的三维模型,并通过UDF用户自定义函数接口将极端运行阵风函数程序导入Fluent中作为流场入口条件,验证了CFD方法模拟极端运行阵风的正确性。Storey等 [15] 基于国际风轮机设计标准IEC61400-1建立了一种极端相关阵风模型,使用数值模拟中的LES方法模拟了一组风力机在极端瞬态风条件下的运行情况。基于此,本文将运用CFD (Computational Fluid Dynamic)中LES的方法,通过Fluent的UDF接口将IEC阵风模型作为流场入口风速条件,将格栅紊流场与IEC阵风模型结合,研究其可行性以及流场特性。
2. 紊流特性参数
紊流场的特性参数主要包括紊流强度、紊流积分尺度以及脉动风速功率谱等。
2.1. 紊流强度
紊流强度是紊流场中最简单但使用最多的参数,紊流强度是指风速根据空间和时间而变化的程度,通常定义为脉动风速的标准差和脉动风速的平均值之比。
(1)
式中:
为脉动风速的标准差,
为脉动风速的平均值。
2.2. 紊流积分尺度
紊流积分尺度是度量紊流场中某一方向上漩涡尺寸平均值的一个指标。格栅紊流场中有包括顺流向、横向以及垂直三个方向的漩涡,每一个漩涡又有x、y、z三个方向的尺度,因此紊流积分尺度一共有九个。紊流积分尺度可由顺流向相邻两点的互相关函数定义,以顺流向的积分尺度为例,其表达式可写为:
(2)
式中:
是脉动风速
和
的方差;
是顺流向相邻两点
和
脉动风速的互相关函数,其中t是时间。但在处理数据过程中,常常引用泰勒尔紊流冻结假说 [16] 假设,即假设漩涡在紊流场中是以平均速度向下游迁移。此时,脉动风速
则可以改写为
,
。公式也可改写为:
(3)
式中:
是脉动风速
的自相关函数。在数据处理过程中,由于自相关系数比较小,会导致泰勒尔假设会有比较大的误差。因此,通常取(3)式的积分上限为
。
2.3. 脉动风功率谱
脉动风功率谱表述的是,紊流的运动能量在不同频率上的分布情况。经过多年来国内外学者对理论与试验的研究,目前有多种类型的脉动风速谱,对于顺流向的脉动风功率谱,常用Von Karman谱 [17] 来描述脉动风速的特性。
(4)
(5)
式中:
是顺流向脉动风速功率谱密度函数;z是地面或水面以上的高度,单位(m);n是顺流向风的脉动频率;
是摩阻速度(剪切速度),单位(m/s);
为摩阻速度修正系数;
为紊流积分尺度,单位(m);U为平均风速,单位(m/s)。
3. 计算模型
3.1. 格栅几何尺寸
便于将数值模拟结果与TJ-2风洞试验数据做对比,本文选用的格栅尺寸与风洞试验中的格栅尺寸相同,水平和竖向单元格栅板条宽度a均为15 cm,格栅板条围成正方形的中心孔,水平和竖向板条之间的净距b均为45 cm。格栅局部示意图如图1所示,水平和竖向均有四个格栅孔,格栅整体示意图如图2所示。
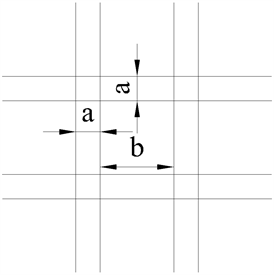
Figure 1. Partial schematic diagram of the grid
图1. 格栅局部示意图
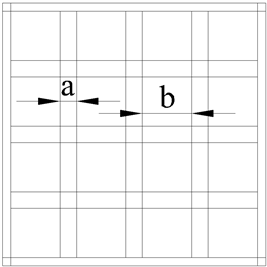
Figure 2. Schematic diagram of the whole grid
图2. 格栅整体示意图
3.2. 模型建立及网格划分
数值模拟格栅紊流场计算域采用三维长方体计算域,宽度为2.4 m,高度为2.4 m,长度为10.5 m,格栅放置于距流场入口4.5 m处。坐标原点位于流场入口的左下方,顺流方向为z正方向,竖直方向为y轴,向上为正,水平方向为x轴,由笛卡尔右手法则确定。计算域示意图如图3所示。
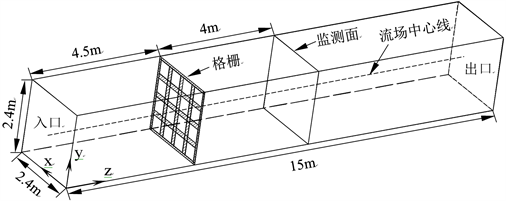
Figure 3. Schematic diagram of calculation domain
图3. 计算域示意图
本文利用Fluent前处理软件Gambit对整个流场域进行网格划分。在格栅附近由于流动比较复杂,为保证结果的精确性,因此需要划分较精细的网格。贴体网格首层高度为0.75 cm,以1.02的增率沿z轴增加。在格栅附近采用非结构化网格对流场域进行划分,其余流场域采用结构化网格划分。格栅附近网格划分示意图如图4所示,整个计算模型网格数量约为330万。

Figure 4. Mesh generation near the grid
图4. 格栅附近网格划分
本文采用大涡模拟(Large Eddy Simulation, LES)湍流模型模拟格栅紊流场。LES湍流模型是通过滤波的方式,把格栅流场中的旋涡分解为大尺度和小尺度旋涡。对于大尺度的旋涡,采用直接计算的方法。而对于小尺度的旋涡,采用压格子尺度(Sub-Grid Scale, SGS)模型进行模拟。在FLUENT求解器中,基于有限体积法(Finite-Volume Method, FVM)求解经过滤波处理后的不可压缩流体连续方程和Navier-Stokes方程。亚格子尺度模型采用Smagorinsky-Lilly亚格子尺度模型,Smagorinsky常数Cs取0.1 [11]。运用SIMPLE算法解决压力与速度耦合问题,压强方程采用二阶迎风差分格式(Second Order Upwind),动量方程采用有界中心差分格式(bounded central differencing)。迭代时间步长取为0.001 s,共计算20,000步,即计算总时长为20 s。计算域的详细边界条件如表1所示。
监测面位于流场下游,距格栅4 m处。监测点间距为0.4 m,均匀布置于监测面内,监测点位置如图5所示。每个监测点记录z方向的风速,采样频率为1000 Hz,采样点数为20,000。
4. 紊流结果分析
本文从每个监测点获得的风速时程曲线进行分析,处理得到格栅紊流场的特性参数。由于流场在刚开始计算时不稳定,导致风速时程曲线的数据没有太大使用价值,因此本文在处理数据时,省去了前两秒的风速时程数据。典型风速时程曲线如图6所示。
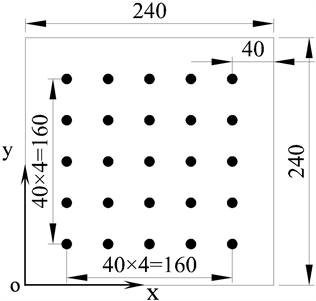
Figure 5. Layout of monitoring points (unit: cm)
图5. 监测点布置图(单位:cm)
图7为格栅紊流场的流线图,可以看出在格栅前为均匀流场。当经过格栅时,由于格栅条是离散布置的,因此,均匀流场被格栅打乱,在格栅后方形成了紊乱的流场。但经过一段距离的发展和扩散之后,流场又恢复了均匀性。
4.1. 紊流强度
格栅紊流场是由均匀流通过格栅装置后形成的,由于格栅条是离散布置的,因此均匀流刚通过格栅时,紊流特性是及其不均匀的。但旋涡经过一段距离的扩散,紊流特性的均匀性逐渐改善,形成各项同性的均匀紊流。本文通过对监测点的风速时程曲线分析得到的紊流强度,来验证格栅紊流场的均匀性。
表2给出了监测面上个点的坐标及紊流强度值,紊流强度最小值为13.4%,最大值为14.9%,平均值为14.3%,标准差为0.004。由此可知,该格栅流场在距格栅4 m的下游处,流场已经达到了较好的均匀性。本文数值模拟的紊流强度,与风洞试验 [8] 中的紊流强度Iu = 15%相比,相对误差为4.67%。与试验数据较吻合,验证本文采用的数值模拟手段是可行的,该湍流场断面可用于开展节段模型的研究。
4.2. 紊流积分尺度
本文同样对监测面上个监测点的风速时程信号进行分析,得到了各监测点的积分长度尺度,详细数据如表3所示。其中最大的紊流积分尺度为0.371 m,最小为0.231 m,平均值为0.279 m,标准差为0.0345,说明该格栅紊流场在此断面处已有足够的均匀性。与文献 [4] 中的结果相比较,相对误差约为16.7%,本文数值模拟结果偏大。其主要原因在于,本文数值模拟的计算条件较差,无法使用庞大数量的网格进行计算。因此导致在数值模拟时,不能捕捉到小尺度的旋涡。
4.3. 脉动风速谱
利用监测点测得的风速时程信号,对其进行傅里叶变换,编写将风速时程信号转化为脉动风速谱的程序,利用MATLAB软件进行处理,即可得到脉动风速谱。本文以顺风向,高度为0.4 m的监测点为例,得到脉动风速谱如图8所示。并Von Karman谱作比较,可以看出数值模拟得到的脉动风速谱,在低频段对比Von Karman谱偏小,但数值模拟的风场能量结构与Von Karman谱基本能够吻合。
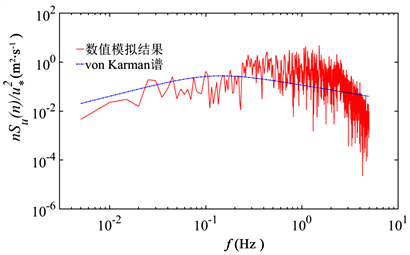
Figure 8. Fluctuating wind speed spectrum
图8. 脉动风速谱
5. IEC阵风与紊流场结合
本文采用Länger-Möller [12] 根据国际通用标准IEC61400-1建立的极端运行阵风(EOG)模型,用作模拟流场入口处的风速:
(6)
式中:Ug为与阵风风速相关的参数;Tg为特征周期时间取10.5 s;U为均匀来流速度。
初始风速为10 m/s,持续时间为15 s时,IEC阵风模型风速时程曲线如图9所示。
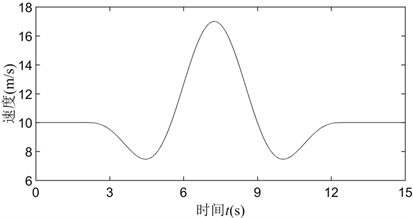
Figure 9. Wind speed time history curve of IEC gust model
图9. IEC阵风模型风速时程曲线
图10为阵风与格栅共同作用下,距格栅4 m的下游流场中心点处,顺流向的风速时程曲线。由于在t = 12.5 s后,IEC阵风风速持续为10 m/s,所以本文仅计算15 s的时长,迭代时间步长为0.001 s。由于刚开始计算时,流场尚未充分发展,因此0~1 s内的风速时程曲线振幅很大。在最大阵风风速时刻附近,紊流场内风速时程曲线振幅也较其他时刻偏大,但整体数值模拟的风速曲线与理论值吻合较好。
图11展示了格栅流场下游4 m处监测面上不同时刻顺流向的速度云图。t = 2.0 s和t = 12.5 s时速度横截面上平均速大致为10 m/s,t = 4.5 s和t = 10.0 s时速度横截面上平均速大致为7 m/s,t = 7.5 s时速度横截面上平均速大致为17 m/s。各时刻风速与IEC理论风速相对应,且监测面上的风速分布均匀,可说明IEC阵风与格栅紊流场结合较好,可在该断面上开展桥梁段面特性的研究。
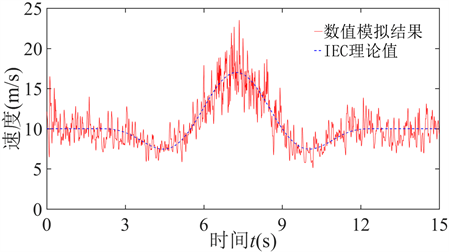
Figure 10. Wind speed curve under the combined action of gust and turbulence
图10. 阵风与紊流共同作用下的风速曲线

Figure 11. Downstream velocity contours at different times at 4 m downstream of the grid
图11. 格栅下游4 m处不同时刻顺流向速度云图
图12是通过CFD后处理软件CFD-POST中的Q-criterion获得的涡量图。当空气经过格栅后,在格栅附近形成较小的旋涡结构,通过一段距离的发展和扩散,漩涡结构逐渐变大。可得出,积分长度尺度是沿顺流向逐渐增大。不同时刻,整个流场区域的漩涡结构分布一致,即在格栅附近为小旋涡结构,而后逐渐变大。IEC阵风的风速变化并不会破坏紊流场的漩涡分布,紊流场与IEC阵风能够很好地结合起来,可用于后续桥梁断面特性的研究。
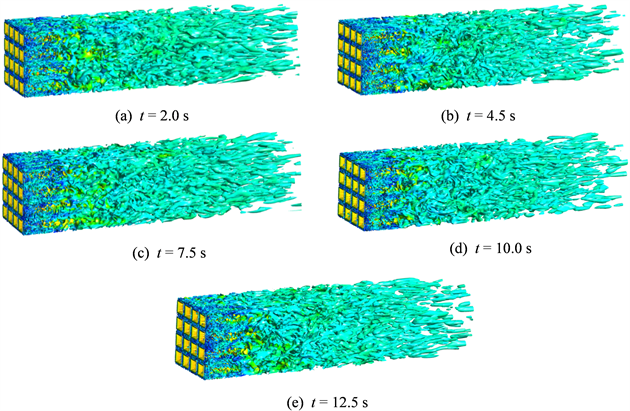
Figure 12. Vorticity contours at different times
图12. 不同时刻的涡量图
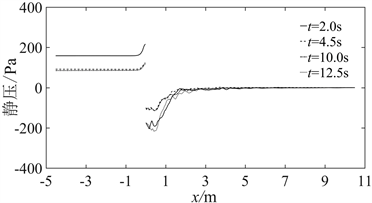
图13为流场中心线上不同时刻的静压图,任意时刻流场中静压仅在格栅附近有较大波动。在格栅前流场中心线上的静压为正,在靠近格栅处急剧上升。在格栅后流场中心线上的静压为负,并快速上升至零。流场中静压与风速密切相关,从IEC风速时程曲线上可以看出,t = 2.0 s和t = 12.5 s、t = 4.5 s和t = 10.0 s时的风速几乎是相同的。因此,图13(a)中t = 2.0 s和t = 12.5 s、t = 4.5 s和t = 10.0 s静压曲线几乎是重合的。图13(b)展示的是t = 2.0 s、t = 12.5 s和t = 7.5 s时流场中心线上的静压曲线,t = 7.5 s时对应的风速最大。因此,格栅前方的正压和格栅后方的负压,分别达到了整个模拟过程的最大值。相反,t = 4.5 s时流场中风速最小,流场中心线上的静压也最小。
 (a)
(a) 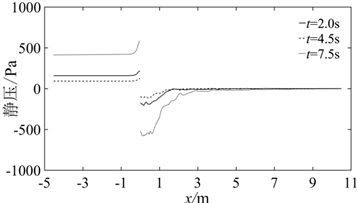 (b)
(b)
Figure 13. Static pressure curve of centerline of flow field
图13. 流场中心线静压曲线图
6. 结论
本文采用LES湍流模型对格栅紊流场和IEC阵风与紊流共同作用下的流场进行了数值模拟,分析流场得到了以下结论:
1) 通过与风洞试验得到的结果对比,发现数值模拟得到的格栅紊流场特性满足要求。数值模拟的方法能够任意布置监测点,并且能直接观察到流场中不同时刻旋涡的分布情况。相对于风洞试验拥有更便于观测、更省时等优点。
2) 数值模拟得到的紊流场紊流强度与风洞试验吻合较好,紊流积分尺度稍微偏大,可能是计算条件不足、网格不够精细导致的,紊流脉动风速谱与Von Karman谱也基本能够吻合。可以利用数值模拟的方法,开展格栅紊流场特性的研究。
3) IEC阵风与紊流共同作用下的脉动风速时程曲线与IEC阵风理论风速曲线吻合较好,不同时刻流场中漩涡结构分布规律一致,不同时刻流场中心线上静压分布规律相同,说明IEC阵风与格栅紊流场结合较好。可用于后续桥梁断面特性的研究。