基于多层前馈神经网络仓储拣货优化问题的研究

Research on the Optimization of Warehouse Picking Based on Multi-Layer Feed Forward Neural Network

摘要: 仓储拣货问题中，实时规划拣货路线一直是难点。由于货架之间互相形成障碍，距离难以用欧氏距离给出，且已知距离后路线规划缺乏行之有效的方法。本文分为两部分，首先采用曼哈顿距离和Kronecker delta给出货架间的距离，将拣货路线转换为TSP (旅行商)问题。第二部分采用性能高、训练快等优点的神经网络智能算法，基于多层前馈神经网络的自适应反馈，形成结果反馈控制和闭环，实现求解TSP问题过程的循环优化。结果发现上述方法简化了拣货路径计算，得到了拣货单的最优拣货顺序及最小距离。

Abstract: In the problem of warehouse picking, it is always difficult to plan the picking route in real time. Due to the barriers formed between shelves, distance is difficult to be given by Euclidean Metric, and route planning after known distance lacks effective methods. This paper is divided into two parts. First, Manhattan distance and Kronecker Delta are used to give the distance between shelves, and the picking route is converted into TSP problem. The second part adopts the neural network intelligent algorithm with advantages of high performance and fast training, and forms the result feedback control and closed-loop based on the adaptive feedback of the multi-layer feed forward neural network, so as to realize the cyclic optimization of the process of solving the TSP problem.

1. 引言

在物流企业的仓储配送作业的流程中，拣货流程是其中至关重要的一个环节 [1]，其效率直接影响整个企业供应链系统的运作效率，对顾客满意度和配送成本有着极为重要的影响 [2]。而提高拣货效率关键在于拣货路径的优化。当拣货员在仓库中拣货时，需要在货格之间、货格与复核台之间、复核台与复核台之间行走。由于这些行走通常要绕过障碍物，故需要设计一种计算货格和复核台之间距离的方法 [3] [4]。同时当拣货员在复核台领取了任务单，需要给出其规划理想的拣货路线。

本文将距离计算分为三个“量子数”进行描述，探究了曼哈顿距离和Kronecker delta对路程计算的简化程度，同时采用CNN (多层前馈神经网络) [5] [6] 对某企业给出的货架距离及拣货单进行了最优拣货路经的计算，得到了最优路径顺序以及最小距离。

2. 曼哈顿距离

曼哈顿距离：两点在南北方向上的距离加上在东西方向上的距离，即

$d\left(i,j\right)=\left|x_i-x_j\right|+\left|y_i-y_j\right|$

对于一个具有正南正北、正东正西方向规则布局的城镇街道，从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离，因此曼哈顿距离又称为出租车距离，曼哈顿距离不是距离不变量，当坐标轴变动时，点间的距离就会不同。

3. 连续Hopfield神经网络

本文运用Hopfield神经网络求解TSP问题，把拣货路线问题的目标函数转化为神经网络的能量函数，把变量(经过的货格)与网络神经元状态相对应 [7]。这样，由于连续型Hopfield神经网络的稳定性理论可知，当网络的能量函数收敛于极小值时，问题的最优解也随之求出，即规划出最短时长的理想拣货路线。

通过对神经元和神经网络进行分析建立模型，用计算机模拟生物神经网络的学习和思考过程，这样的网络叫做人工神经网络(ANN)。ANN按照信息流可以分为前馈式和后馈式，本文运用的连续Hopfield神经网络(CHNN)属于反馈式神经网络，适用于处理组合优化问题。

使用Hopfield神经网络的CHNN模型，将网络抽象等效为放大电子电路。利用模拟电路(电阻、电容以及运算放大器)实现了对网络的神经元的表述。CHNN电路形式如图1所示：

Figure 1. Curve: CHNN circuit form

图1. CHNN电路形式

依据设计思路，将TSP问题映射为一个连续型Hopfield神经网络主要分为以下几个步骤，如图2所示：

Figure 2. Curve: Mapping step

图2. 映射步骤图

当CHNN的结构和参数设计完成后，迭代优化计算过程将会变得容易。具体步骤如图3所示。

4. 距离优化模型

4.1. 基于曼哈顿距离和改进的A-Star算法构建距离模型

由于曼哈顿距离是对于一个具有正南正北、正东正西方向规则布局的城镇街道的公式，与本题的竖直与水平方向相符，故使用曼哈顿距离来刻画货格之间、货格与复核台之间、复核台与复核台之间的距离．当拣货员在仓库中拣货时，需要在货格之间、货格与复核台之间、复核台与复核台之间行走．需要分三种情况讨论：

1、货格与货格之间：

$S_1=x+y+d_{\text{corner}}$

借鉴量子力学中描述原子的状态有四个量子数，即用四个变量来表示状态。所以这里本文选用横坐标x，纵坐标y，转角数 $d_{\text{corner}}$，这三个量子数来表示。

其中x表示为横坐标的变化，y表示纵坐标的变化， $d_{\text{corner}}$ 表示拐角数的变化。

Figure 3. Curve: The CHNN model iteratively optimizes the calculation process

图3. CHNN模型迭代优化计算过程

通过曼哈顿距离公式，我们得到如下三个量子数的规律：

(1) 横坐标x的变化规律，均为

$x=\left|x_j-x_i\right|$

(2) 纵坐标y的变化规律分为两种情况：

这里本文采用改进的A-star算法计算最短路径即距离最短。A-star算法是一种静态路网中求解最短路径最有效的直接搜索方法，也是解决许多搜索问题的有效算法。算法中的距离估算值与实际值越接近，最终搜索速度越快。公式表示为：

$f\left(n\right)=g\left(n\right)+h(\; n\; )$

其中，f(n)是从初始状态经由状态n到目标状态的代价估计，g(n)是在状态空间中从初始状态到状态n的实际代价，h(n)是从状态n到目标状态的最佳路径的估计代价。

当 $t_m=t_n$ 时，即为同一排时，可以走上，下两个方向的路线，分别为

$f_1=\{\begin{array}{l}\left|y_j+y_i-\left(l_0+2l_1\left(k-1\right)\right)\right|,y_j+y_i<e{d}_2+d_3+\left(l_0+2l_1\left(k-1\right)\right)\\ 2e{d}_2+2d_3-\left|y_j+y_i-\left(l_0+2l_1\left(k-1\right)\right)\right|,y_j+y_i>e{d}_2+d_3+\left(l_0+2l_1\left(k-1\right)\right)\end{array}$

其中k表示为自下而上的某一排， $l_0$ 表示为第一排与复核台之间的中心线与横坐标轴的距离， $l_1$ 表示为相邻两排的中心线与相邻的相邻两排中心线的距离， $d_2$ 表示为货格长宽， $d_3$ 表示为竖直方向相邻两排货架纵向距离，e为每个货架的货格数。

将采用改进A-star算法，其主要原因为：A-star算法具有较小的空间复杂度、时间复杂度，能在短时间内获得最优路径；A-star算法作为启发式算法具有较强的适应能力，可以根据实际的约束条件来调整启发函数；

在本文所取得启发函数为曼哈顿距离函数，即 $h\left(n\right)=f_1$，并取 $g\left(n\right)=1$ (因为无论路径，拣货员每次移动的距离均相同)，则

$f\left(n\right)=g\left(n\right)+h\left(n\right)=1+\{\begin{array}{l}\left|y_j+y_i-\left(l_0+2l_1\left(k-1\right)\right)\right|,y_j+y_i<e{d}_2+d_3+\left(l_0+2l_1\left(k-1\right)\right)\\ 2e{d}_2+2d_3-\left|y_j+y_i-\left(I_0+2l_1\left(k-1\right)\right)\right|,y_j+y_i>e{d}_2+d_3+\left(l_0+2l_1\left(k-1\right)\right)\end{array}$

其中，f(n)是从初始状态经由节点n到目标节点的距离估计，g(n)是在状态空间中从初始节点到节点n的实际距离，h(n)是从节点 n 到目标节点的最佳路径的估计距离。

当 $t_m\ne t_n$ 时，即不是同一排时，均为

$f_2=\left|y_j-y_i\right|$

即纵坐标y的变化规律为

$y=\{\begin{array}{l}\left|y_j+y_i-\left(l_0+2l_1\left(k-1\right)\right)\right|,y_j+y_i<e{d}_2+d_3+\left(l_0+2l_1\left(k-1\right)\right)\\ 2e{d}_2+2d_3-\left|y_j+y_i-\left(I_0+2l_1\left(k-1\right)\right)\right|,y_j+y_i>e{d}_2+d_3+\left(l_0+2l_1\left(k-1\right)\right),t_m=t_n\\ \left|y_j-y_i\right|,t_m\ne t_n\end{array}$

(3) 转角的变化规律分为两种情况：

是否同列：若 $r=\left|x_j-x_i\right|=2d_2$ 则两货格处于同列。定义 $\delta \left(r\right)$ ：若二者同列，返回值为0；不然，则为1。

是否同侧：若 $\omega =\frac{\left|x_j-x_i\right|}{2d_2+d_3}=Z^{+}$ ( $Z^{+}$ 表示为正整数)，则两货格处于同侧。定义 $\delta \left(\omega \right)$ ：若二者同侧，

则返回值为0；不然，则为1。

由于货架排数的变化不会对拐角有任何影响，故有如下公式：

$d_{\text{corner}}=d\left(2+2\delta \left(\omega \right)+2\delta (\; r\; )\right)$

其中 $d_1$ 表示为水平方向每组货架之间的距离，d表示为当绕障碍物折线行走时横向和竖向偏移。

本文赋予以下说明：当 $t_m=t_n$， $\left|x_j-x_i\right|=2d_2$ 或0， $x_j=x_i$ 时，即同排同列同侧时相邻两个货格的距离会有两个转角的增加。在附件四：计算结果中，同排同列同侧的相邻两货格之间的距离 $d_0=800\text{mm}+2\times d=800\text{mm}+2\times 750\text{mm}=2300\text{mm}$，而不仅仅两个货格间的垂直距离是800 mm。

2、复核台与复核台之间：

根据题中所描述的复核台之间距离简化为两复核台坐标差的绝对值之和，即

$S_2=\left|x_j-x_i\right|+\left|y_j-y_i\right|$

3、货格与复核台

若复核台在左边，我们假设复核台的右边长距离货格最近，且 $\delta \left(l\right)$ 返回值为1；若复核台在下边，我们假设复核台的上边长距离货格最近，且 $\delta \left(l\right)$ 返回值为0。即

$S_3=\left|x_j-x_i\right|+\left|y_j-y_i\right|+d\left(3+\delta \left(1\right)\right)$。

4.2. CHNN模型的优化求解连续Hopfield神经网络的优化模型

任务单T0001中共有23个订单，随之对应23个商品货格．随机产生的初始路径如图4所示：

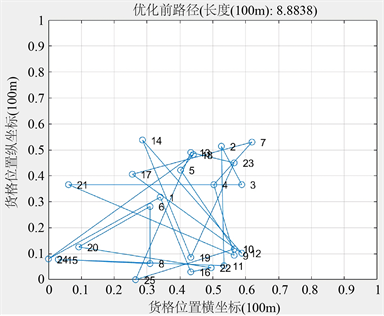
Figure 4. Curve: Randomly generated initial path

图4. 随机产生的初始路径

当前任务单T0001的拣货路线长为888.38 m。经连续型Hopfield神经网络优化后，产生的最优途径如图5所示：

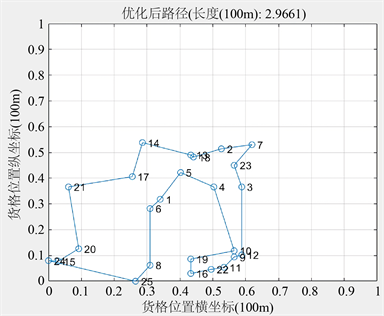
Figure 5. Curve: Optimized path of continuous Hopfield network

图5. 连续Hopfield网络优化后的路径

未进行优化前的路径为888.38 m，优化后的最优拣货路线长为296.61 m，路线长度降低了66.61。能量函数随迭代次数变化的曲线如图6所示：

Figure 6. Curve: Graph the energy function

图6. 能量函数变化曲线图

从图中可以看出，神经网络的能量随着迭代次数增加不断减少。当能量变化值趋于0时，神经元状态也趋于平衡。此时，所求得的路径为任务单T0001理想的拣货路线。本着距离优先原则，综合上图分析，计算出T0001任务单中货格与复核台FH10距离最近的一个货格作为起始货格。终止复核台为最近的FH02。按照上图，理想拣货路线的路线为：FH10 → 24 → 20 → 21 → 17 → 14 → 13 → 18 → 2 → 7 → 23 → 3 → 12 → 9 → 11 → 22 → 16 → 19 → 10 → 4 → 5 → 1 → 6 → 8 → 25 → 15 → FH02 (数字为上图中任务单T0001商品按大小排序的序号)。

基金项目

MathorCup高校数学建模挑战赛组委会基金资助。