1. 引言
目前偏微分方程数值求解通常采用有限节点差分FDM方法,其可以保持较高精度,但随着智能算法如神经网络、遗传等不断发展,在偏微分方程有所应用 [1]。如Lagaris, Isaac E早期首次将ANN应用在偏微分方程,但由于年份较远,细节论证讨论相对不清晰 [2]。杨云磊对常微分方程进行了数值求解,但仅讨论了常微分方程(ODE),并且为强制边界 [3],康奈尔大学MALLS也将常微分方程进行了数值求解,并讨论了收敛机理 [4],但上述仅讨论ODE,未提及偏微分方程求解计算与权重函数迭代增量收敛性故不具备较深参考性。因此为完善ANN计算应用,本文对Lagaris早期发表的文献进行复算与更详尽说明,并对双曲方程做了求解应用,更好地明晰了求解过程,但对非稳态及耗散与CFD格式精度关联还需后续进一步探讨研究。
2. 分析
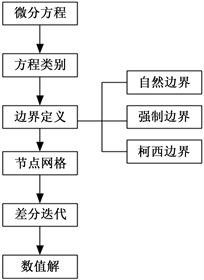
目前FDM对求解PDE方法较为成熟,对一般偏微分方程通常采用有点差分法,通过节点加密并迭代求得数值解。而ANN采用改变过程变量权重,并经过训练以达到数值解,具体流程见图1(a)~(d),这里不再系统阐述。
3. 具体案例求解
例1 求解非其次泊松方程(文献 [2] problem7)以计算求解:
其中FDM方法采用五点差分方法Gauss迭代与神经网络结果见图2(b),其中训练次数T = 1,T = 10,T = 50三种,其中激活函数采用
,其中
。
 (a)
(a) 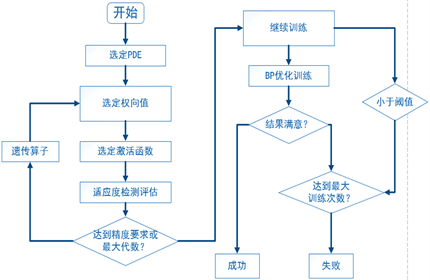 (b)
(b)  (c)
(c)  (d)
(d)
Figure 1. (a) Solution flow of FDM method; (b) ANN solution process; (c) ANN process; (d) ANN method weighting process
图1. (a) FDM方法求解流程;(b) ANN方法求解流程;(c) ANN流程;(d) ANN方法加权过程
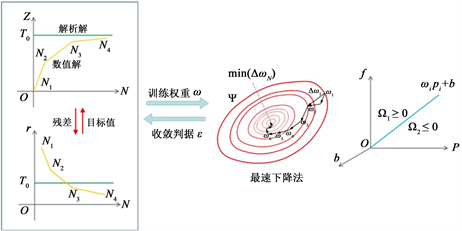
具体测试参数设置见表1,从表1得出,影响计算关键精度主要在于权重w,
为每次权重变化率即(
),当权重变化量。最右侧表示:最大权重增量梯度,以表征权重变化梯度,并且介于(0-1)区间。

Table 1. Description of ANN method parameter setting and solution results
表1. ANN方法参数设置与求解结果说明
例2 选定文献problem5。
,
,
,
,
求解过程与例1相同,结果见图3。
表2 problem5例求解参数设置与结果说明。

Table 2. Solution parameter setting and solution result description
表2. 求解参数设置与求解结果说明
例3 求解稳态二维Burgers双曲方程根据文献 [5]。
,边界
其解析解为:
由于是稳态求解,另时间t=0,需要说明由于边界与文献边界不同,因此公式需要修正。
结果如下:
化简后:
同时,为了简化问题取t = 0初始时刻,以求解稳态方程。
 (a)
(a)  (b)
(b)  (a)
(a)  (b)
(b)
Figure 4. (a) Analytic solution image; (b) ANN solution results (T = 10); (c) ANN solution results (T = 100); (d) ANN solution and analytic solution residue (T = 100)
图4. (a) 解析解图像;(b) ANN方法求解结果(T = 10);(c) ANN方法求解结果(T = 100);(d) ANN方法求解与解析解残差(T = 100)
Burgers双曲方程参数设置与求解结果见表3。

Table 3. Parameter setting of the solution method and description of the solution results
表3. 求解方法参数设置与求解结果说明
通过计算可知,ANN同样适用与双曲方程但求解精度有所下降,这与双曲方程不稳定性有关(库朗数CFL < 1)。但由于本案例处理稳态问题,因此得出ANN对稳态双曲同样适用,但处理非稳态问题还需再探讨。图4(c)结果偏小是由于ANN训练结果从下界逼近真实解析解。
4. 讨论
根据上述计算结果可知,对ANN求解偏微分方程精确,需要对权重函数进行约束,即
,
,
递减,
求解采用最速下降法。
ANN方法可求解出精度较高的数值解。具体流程及求解时间见图5,对于求解步骤见表4。
 (a)
(a) 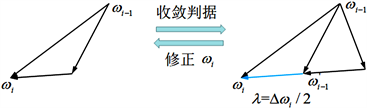 (b)
(b)
 (c)
(c)
Figure 5. (a) ANN solution process; (b) Weight function solution process correction; (c) Is the relationship between training times and solution time; (d) Comparison of solution time
图5. (a) ANN求解流程;(b) 权函数求解过程修正;(c) 训练次数与求解时间关系;(d) 求解时间比较
5. 结语
本文目前论述了人工神经网络ANN与经典有限元FDM求解偏微分方程的区别,得出了以下结论:
1) 采用高斯经典FDM在处理偏微分方程问题时,求解时间较短,但本文只对椭圆型以双曲稳态方程进行了验证,因此FDM方法与ANN方法求解偏微分方程优势较大需要后续更深入研究。
2) ANN方法求解精度取决于权重w设定,变化
愈小求解愈精确,其激活函数修正对计算结果影响较小。
3) 偏微分方程求解精度需要对权重变化率
设定约束条件。
4) 通常求解到
小于0.1时,求出数值解与解析解误差相对较小。
5) 对二维双曲Burgers方程进行了稳态求解,但对非稳态时变效应及耗散问题还需后续进一步探讨研究。
致谢
在此对本文提出修改意见的专家表示感谢,以及对魏大盛和王海辉两位老师对本文的指导提出由衷地感谢!
NOTES
*通讯作者。