基于复杂网络的城市地下管线普查区域划分

A Zoning Method Based on Complex Networks for Urban Underground Pipeline Survey

摘要: 面对城市地下管网普查工作中传统格网分区方法的缺陷，本文以给水管网为研究对象，提出了基于社区发现的划分方法。首先，在分析管网的空间分布特征的基础上，构建管网对偶图数据模型，通过裁剪算法提取管网的主干网络；然后，基于社区发现算法，迭代生成管网的最小分区单元；最后，以管网的长度约束条件，进行社区子团合并，形成有效的管网分区。实验结果表明，本文提出的基于复杂网络的分区方法，保证了管线实体的完整性和整体管网的社区结构，可有效支撑管网普查实际工作。

Abstract: To address the shortcomings of the traditional grid zoning method in urban underground pipe network survey work, in this paper, we propose a community discovery-based zoning method based on the study of water supply networks. First, we analyze the spatial distribution characteristics of the pipe network, construct the dual graph model of the pipe network, and extract the backbone network of the pipe network by a trimming algorithm. Then, based on the community discovery algorithm, we iteratively generate the smallest partition unit of the pipe network. Finally, with the constraint of the length of the pipe network, the community subgroups are merged to form an effective pipe network zoning. The experimental results show that the zoning method based on complex networks proposed in this paper ensures the integrity of the pipeline entities and the community structure of the overall pipeline network, which can effectively support the actual work of the pipe-line network survey.

1. 引言

地下管线是城市重要的基础设施，被称为城市“生命线” [1]。随着城市规模的不断扩张，地下管线新旧混杂，网络结构日趋复杂化。由于缺乏全面的管线信息，特别是准确的空间位置信息，各种安全事故常有发生，甚至导致重大经济损失。在加强管线科学规划、信息化管理的同时，对现有城市地下管线的普查和探测工作也越来越受到重视。如何科学、有效地对管网进行区域划分是管网普查的关键问题。

管网分区能有效的降低管网的规模和复杂程度，是管网设计、分析等研究的基础问题。Yazdani等应用复杂网络研究供水管网结构特征，提出了管网扩建的策略 [2]。徐丽君等基于实体间的拓扑关系对燃气管网数据进行增量分区 [3]。研究者从管网的网络特性出发，结合行业的领域知识展开了各类地下管线的分区研究。随着复杂网络的社区发现研究的兴起，将社区计算与管网分区相结合产生了一系列研究成果，张正培利用网络搜索算法对环流网结构中的社区结构进行挖掘 [4]。王彤在简化供水管网的基础上，提出了基于社区算法的供水管网区块化方法 [5]。然而，现有管网分区的技术主要是针对管网设计、分析等问题，出于降低管网的规模和复杂程度，通常建立在管网简化的基础上，应用于城市新增管网的规划以及针对已有管网的压力分区优化等方向。但从现势管网普查出发，对城市地下复杂管网进行分析与建模，而进行的管网分区研究鲜有涉及；顾及管网的完整性和拓扑结构特征，以满足普查分区中有特定工作区数量的需求，缺少针对性研究。

地下管网普查是对某一区域内的地下管线敷设现状进行的全面调查 [6]。传统的管网普查时，通常采用人工划定普查区域或者是基于地图图幅的规则格网方式进行分区。不仅仅破坏了管网的整体拓扑连通性，造成了普查管段的不连续；同时忽略了区域内部管网的结构，导致了基于分区的普查工作量分配不均衡，间接增加了普查出现错误的可能性。因此，面对地下管网普查时，如何科学、有效地对管网进行区域划分是管网普查具体作业中的关键问题。本文以给水管网为研究对象，分析给水管网的空间结构特征，将社区发现算法与管网长度约束相结合，探讨面向城市地下管线普查时的分区方法。

2. 给水管网分区方法

2.1. 基于对偶图模型的主干管网提取

给水管网空间数据常用“节点—弧段”式矢量模型来表达管网中的管线和管点，如图1(a)。由于数据采集、数据处理等原因，一条实际管段被分割为多条弧段表示。虽然“节点—弧段”能够表达数据的几何形态，但这种“琐碎”方式具有数据冗余、拓扑连接呈现均质化和规则化等明显的缺陷。在复杂网络的结构分析研究中，为了更好的表达节点之间的联通关系，通常采用对偶图模型来表达网络拓扑结构 [7]。将线抽象为节点，从而连接形成的无向图称之为网络的对偶图。与传统矢量数据相比，对偶图节点间的连接代表网络中两条边之间的连通关系，能够保持网络的整体结构形态，具有无标度特征，广泛应用于道路网匹配、社交网络挖掘等研究领域。为了分析给水管网的结构特征，本文引入管网对偶图模型，通过将管网中的管段抽象为边，形成对偶图，如图1(b)。

Figure 1. Pipe network data model: (a) Pipe network vector data model; (b) Vector dual graph model of pipe network

图1. 管网数据模型：(a) 管网矢量数据模型；(b) 管网矢量对偶图模型

面向管网普查工作时，与用户直接关联的末梢管网是重要的普查对象，管网细节的精确程度是普查工作指标之一。因此，直接移除或合并管段在本文研究中不能直接适用。经过上文对于管网的空间特征分析可知，大量的树状结构管网是依靠一个关键节点与主干网相连接。裁剪管网中的树状结构，将裁剪掉的管网长度赋权值于主管网中相应的节点，则在保证整体管网数据完整性的基础上，完成了管网的主干网的提取。对偶图模型中的树形结构满足以下特征：1) 任意两个节点之间可达；2) 任意两个节点有且只有一条通路；3) 一个节点的前驱和后继关联节点中有一方至多只有一个节点。其提取算法如下(Degree为节点所关联的边数)：

2.2. 基于社区发现算法的管网分区

给水管网是典型的复杂网络，社区结构是复杂网络的一个普遍特征。因此，给水管网的剖分可以采取如下思路，使用社区发现算法将给水管网划分成若干原子社区，或称为最小分区单元。然后，按照分区的长度指标进行最小分区单元的聚合。从而，达到理想的分区状态，即使分区内的管线里程尽可能均匀分布。所以，本文分区方法的重要基础工作是对环状主干管网进行最小分区单元的划分。

基于Fast Unfolding社区发现算法实现。设图 $G=G\left(V,E\right)$，社区发现即在图G中确定 $nc\left(\ge 1\right)$ 个社区， $C=\left\{C_1,C_2,\cdots ,C_{nc}\right\}$，使得各个社区的顶点集合构成顶点V的一个覆盖。将管点指定到一个唯一的社区，按照顺序将节点在这些社区之间进行移动，若节点i有三个邻居节点j1、j2、j3，分别尝试将节点i移到jx所在的社区，并计算相应的模块度差值 $\Delta Q_x$，将i移动到 $\Delta Q$ 取最大值的社区(正值才移动，负值不移动)。模块度差值的计算公式如下：

$\Delta Q=\left[\frac{{\displaystyle \sum in}+2k_{i,in}}{2m}-\left(\frac{{\displaystyle \sum tot}+k_i}{2m}\right)\right]-\left[\frac{{\displaystyle \sum in}}{2m}-{\left(\frac{{\displaystyle \sum tot}}{2m}\right)}^2-{\left(\frac{k_i}{2m}\right)}^2\right]$ (1)

其中， ${\displaystyle \sum in}$ 是社区C内的权重之和， ${\displaystyle \sum tot}$ 是连接社区的外部连接的权重之和， $k_i$ 是连接节点i的外部连接的权重之和， $k_{i,in}$ 是i与内部节点的连接权重相加的和，m为整个网络的权重之和。将第一阶段得到的社区视为新的节点，重新构造子图。两个新节点之间的变得权重为相应两个社区之间的各边权重的总和。将两个阶段合起来的一个操作为一次迭代，该方法明显呈现出层次结构，同时这种将边的权重赋予节点的方法框架，便于下一步的社区聚合。模块度(Modularity)通常被用来评价社区分割的优劣 [8]，其指网络中连结社区结构内部顶点的边所占的比例与另外一个随机网络中连接社区结构内部顶点所占比例的期望相减的差值，计算公式如下：

$Q={\displaystyle \underset{c\in C}{\sum }\left(\frac{l_c}{m}-{\left(\frac{D_c}{2m}\right)}^2\right)}$ (2)

其中，m为图G中的总边数， $l_c$ 为社区c中的所有内部边的总条数， $D_c$ 为社区中所有顶点的度之和，且 $D_c=2L_c+O_c$， $O_c$ 是社区c与其他社区的边。Q值的范围在 $\left[-0.5,1\right)$，模块度越大则表明社区划分效果越好。

2.3. 基于SLPA框架的社区子团合并

由于社区发现算法的收敛条件主要顾及管网的拓扑性质，划分出来的管网单元大小不一，长度分布并不均匀。此外，从实际管网普查的角度，无法指定的分区数目不利于合理安排管网的普查工作。所以，在最小社区子团的基础上，结合树状管网的权重，进行子团聚合，最终达到较为合理的分区结果。管网社区子团的聚合，可视为一种社区标签的传播，使用更高级别的标签来替代低级别的标签，从而形成管网的层次结构。本文采用SLPA (Speaker-Listener Label Propagation)框架，自定义基于管线长度的标签选取规则，实现管网的可控聚合。SLPA作为一种重叠型社区发现算法，通过适当的规则定义，将重叠型社区退化为非重叠型社区。SLPA引入了Listener与Speaker两个概念，在更新节点标签的过程中，选取一个节点作为Listener，其所有邻居节点都为Speaker，依照自定义的规则确定跟从Speaker的标签。对于环状管网，将每个节点挂载的子团的权重赋与该节点，并对每一个节点进行T次迭代，构造SLPA矩阵。

按照节点的顺序，记录每一个节点在刷新迭代过程中的历史标签序列，当迭代停止后，对每一个节点的历史标签出现的频率进行统计，按照阈值过滤掉其他的标签。选取的规则为：由权重较小的节点作为Listener，遵循其邻居节点的标签，当出现多个标签时，优先听从权重较低的节点，实现自下而上的子团合并。如图2所示，一个社区子团构成的拓扑网络共有共计8个社区，按照定义的规则，逐次确定每个节点的标签等级。第一次迭代，选择环状节点上挂载有叶子节点的节点，按照裁剪的方式再合并子团，所以c归属于b、g和h归属于e，此时把整个环网分成四个部分；第二次迭代，选择最小的节点a作为Listener，其归属于权重最低的邻居节点b或d，此时为三分环网的方案；以此类推，将d、e合并，形成管网的二分方案；最终所有社区子团收敛到一个代表管网整体的节点。

Figure 2. Community aggregation process

图2. 社区聚合流程

3. 实验与分析

选取了南京市局部给水管网进行分区实验，覆盖面积约为10.2平方公里，管网总长度为102.78 km，如图3(a)所示。以管点为节点，管段为边，管段长度为边的权重建立拓扑结构图。从拓扑结构上看，树状结构大多数出现在居民小区内部，环状结构贯穿于整个网络。整个管网呈现出树状结构挂载在环状主干网上的形态。通过社区发现算法进行最小子团的划分，当模块度为0.94时，达到收敛平衡，共得到11个最小单元，如图3(b)。

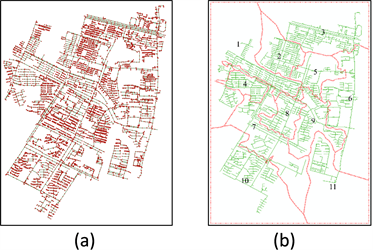
Figure 3. (a) Study area; (b) Minimum zoning unit distribution

图3. (a) 实验区域；(b) 最小分区单元分布

Figure 4. Comparison of partition results: (a) Proposed method; (b) Traditional grid zoning

图4. 城市地下管网分区对比：(a) 本文方法划分结果；(b) 传统格网划分结果

假设设定分区数为5，则经过聚合形成结果，如图4所示，分区中管网长度分别为20.43 km、21.34 km、18.5 km、21.61 km以及20.01 km，各分区长度相近。基于长度的SLPA规则，较好地保证了分区内管点管段数目和管网长度的平衡均匀分布。且该划分方案是一个逐步收敛的过程，可以指定任意的分区数目，从而规避了人为因素干扰分区效果的情况。对比传统格网划分方法，不仅区域内管网长度大小不一，而且割裂连续的管段，不利于对管线实体的提取与分析。

4. 结束语

本文提出了一种城市地下管线普查区域划分方法，采用“先离散再聚合”的思路，离散即通过社区发现来寻找拓扑结构上保持连续性的最小分区单元，聚合即按所需分区数量进行有约束条件下的最小分区单元聚合。与传统的格网分区方法不同，该方法基于复杂网络模型，充分保证了管线实体的完整性和整体管网的社区结构特征，以拓扑关系和长度作为分区依据，取得了良好的效果，可在城市地下管网普查中发挥积极作用。值得指出的是本文方法中使用的是无向网络，引入有向加权网络将是下一步研究的重点工作。