Pasternak地基对FGM圆板非线性弯曲的影响

The Influence of Pasternak Foundation on the Nonlinear Bending of FGM Circular Plate

摘要: 功能梯度材料结构由于容重轻，机械强度高，常常应用于飞机、滑翔机等的航空板中。本文研究了Pasternak地基对FGM圆板在横向载荷下非线性弯曲行为的影响。假设功能梯度材料性质只沿梁厚度方向并且按成分含量的幂指数形式变化；为消除材料非均匀性导致的拉弯耦合效应，引入了物理中面，给出了地基弹性模量kw和地基剪切模量kp对FGM圆板变形的关系，分析了材料梯度指数对不同地基板的影响。结果表明：地基弹性模量是影响FGM板变形的主要因素，kw越大，板的变形越小；材料中金属成分越多，板的变形越大；kw越大，梯度指数对FGM圆板变形的非线性影响越小。

Abstract: Functionally gradient materials (FGM) are often used in aircraft, gliders and other aircraft plates due to their light bulk density and high mechanical strength. The influence of Pasternak foundation on the nonlinear bending behavior of FGM circular plate under transverse load was studied in this paper. It is assumed that the properties of FGM only change along the thickness of plate and change according to the power law distribution with the volume fraction of the constituents. In order to eliminate the tension-bending coupling effect caused by material inhomogeneity, the Physical middle plane was introduced. The relationships between elastic modulus of foundation and shear modulus of foundation on deformation of FGM circular plate were given, and the influences of material gradient index on different ground plates were analyzed. The results show that the elastic modulus of foundation is the main factor affecting the deformation of FGM plate, and the larger the elastic modulus kw is, the smaller the deformation of FGM plate is; The more metal components in the materials, the greater the deformation of the plate will be; The larger kw is, the smaller the nonlinear effect of gradient index on the deformation of FGM circular plate is.

1. 引言

航空胶合板由材质均匀、强度高的木材旋制的薄单板。鉴于功能梯度材料(FGM)具有耐高温，抗腐蚀，强度高，韧性好等优点 [1]，目前已被广泛用来作为高温及恶劣环境下工作的结构构件,在航空航天等实际工程中备受关注 [2]。因此，FGM材料代替传统材料制作的航空板具有极大的应用前景。另外，FGM板还适用于航空军事工业中的仪器、仪表、高低压开关柜面板等结构中。为防止结构由于受到外力的冲击而发生破坏或较大变形，需要在圆板上增加不同的弹性地基。因此，有必要对弹性地基上的FGM圆板的非线性力学行为进行详细的分析。从而为航空工业结构设计及应用提供必要的理论依据。

国内外学者采用不同的弹性地基模型，研究了地基系数对板屈曲或弯曲的力学行为做了大量的工作。文献 [3] 基于经典板理论，研究了在winkler弹性地基上的线性变厚度极正交各向异性圆板的轴对称振动问题。李世荣等 [4] 研究了winkler弹性地基及均匀升温作用下弹性圆板的轴对称热过屈曲问题，分析了地基刚度参数临界屈曲温度载荷及过屈曲平衡构形的影响。文献 [5] 研究了winkler弹性地基上弹性圆形复合板在突发局部荷载作用下的轴对称振动问题。Fatemeh Farhatnia等 [6] 基于正弦剪切理论，研究了winkler地基上FGM后圆板在热/机载荷下的非线性弯曲问题，分析了地基刚度系数对板变形的影响。

工程实际中，由于水平力作用必然会导致地基与结构接触面上存在切向方向的相互作用，因此没有考虑切向力的Winkler模型与实际问题不符。为了克服Winkler模型不足，马立博等 [7] 提出了一种三参数弹性地基梁模型，计算结果表明：三参数地基模型比Winkler模型更加符合工程实际。之后，学者们对Winkler地基模型进行了不同方法的改进 [8]。然而，这些模型均未能考虑地基在切向和竖向地基反力作用下纵横方向变形以及振动的耦合特性。文献 [9] 考虑了水平摩阻力，分析了竖桩支撑的弹性地基梁的变形。这个模型比较接近工程实际，但也只局限于线性弹性地基梁。文献 [10] 研究了非线性弹性地基上梁在随动载荷作用下的屈曲和振动问题，考虑了梁和非线性弹性地基水平以及竖向的耦合影响，结果表明：线性刚度的影响大于立方刚度的影响。张大光 [11] 基于物理中面与高阶剪切变形理论，用Ritz法分析了双参数弹性地基上FGM梁非线性弯曲响应。讨论了地基参数变化对FGM梁力学行为的影响。

在上述研究的基础之上，考虑水平摩阻的Pasternak地基模型被许多学者所采用。边学成 [12] 等克服了Winkler地基模型无法考虑路基填料和地基中应力扩散的缺点，采用双参数的Pasternak模型研究路面荷载作用下土工格室加筋体的受力与变形机理。刘飞禹 [13] 等采用Pasternak地基模型模拟路基特性,运用有限元方法进行组装并采用迭代法进行求解, 得到路面结构在不同地基系数下的变形结果。研究结果表明：水平摩阻的影响不能忽略。Tahouneh [14] 等研究了任意边界条件下Pasternak弹性地基上连续梯度纤维增强环板三维振动问题。

大量的文献调研表明：各种弹性地基上梁结构的静动态力学响应分析较多，相比之下，弹性地基上板的弯曲和屈曲分析较少，尤其是FGM圆板在Pasternak弹性地基上的非线性弯曲行为的研究鲜见。鉴于此，本文给出了Pasternak弹性地基上FGM圆板在横向均匀载荷下的非线性弯曲控制方程，引入物理中面的概念消除了非均匀材料引起的拉弯耦合效应，数值计算了双参数弹性地基系数对FGM圆板弯曲响应的影响。

2. 基本方程

考虑置于Pasternak双参数弹性地基上的周边夹紧FGM薄圆板了，其厚度为h，半径为a，圆板上受到横向均布载荷q的作用。采用笛卡尔坐标系 $\left(r,\theta ,z\right)$，这里设r为径向且并由板中心向外为正， $\theta$ 为环向，z轴正方向垂直于平面向上，如图1所示。圆板由陶瓷和金属复合而成的功能梯度材料制成。

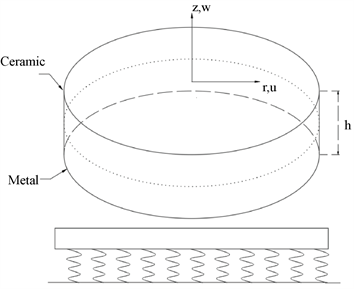
Figure 1. FGM circular plate on Pasternak foundation

图1. Pasternak地基上的FGM圆板

2.1. 几何方程

由于FGM材料的非均匀性，导致几何中面和物理中面不重合，为消除FGM材料中拉弯耦合效应，引入如下物理中面 [15]

$z_0=\frac{{\displaystyle {\int }_{-0.5h}^{0.5h}zE\left(z\right)dz}}{{\displaystyle {\int }_{-0.5h}^{0.5h}E\left(z\right)dz}}$ (3)

根据经典板理论，圆板的位移函数表示为：

$u_r\left(r,z\right)=u\left(r\right)-\left(z-z_0\right)w_{,r}$， $u_z\left(r,z\right)=w\left(r\right)$ (4)

非线性几何关系为：

$\{\begin{array}{l}{\epsilon }_r={\epsilon }_r^0+z{\kappa }_r=u_{,r}+w_{,r}/2-\left(z-z_0\right)w_{,rr}\\ {\epsilon }_{\theta }={\epsilon }_{\theta }^0+\left(z-z_0\right){\kappa }_r=u/r-\left(z-z_0\right)w_{,r}/r\end{array}$ (5)

考虑对称性，FGM圆板的本构方程为：

$\left(\begin{array}{c}{\sigma }_r\\ {\sigma }_{\theta }\end{array}\right)=\frac{E\left(z\right)}{1-{\nu }^2}\left[\begin{array}{cc}1& \nu \\ \nu & 1\end{array}\right]\left(\begin{array}{c}{\epsilon }_r\\ {\epsilon }_{\theta }\end{array}\right)$ (6)

应力沿着板厚度方向积分，可得薄膜力和弯矩为

$\left(N_i,M_i\right)={\displaystyle {\int }_{-h/2}^{h/2}{\sigma }_i}\left(1,\left(z-z_0\right)\right)\text{d}z$， $\left(i=r,\theta \right)$ (7)

式中 ${\epsilon }_r,{\epsilon }_{\theta }$ 和 ${\sigma }_r,{\sigma }_{\theta }$ 分别为径向和环向的应变和应力； $N_i\left(i=r,\theta \right)$ 为薄膜力， $M_i\left(i=r,\theta \right)$ 为弯矩。将式(5)代入式(6)，考虑到式(4)，得到

$\left(N_r,M_r\right)=\left(A,B\right)\left[u_{,r}+\frac{1}{2}{w}_{,r}^2+\nu \frac{u}{r}\right]-\left(B,D\right)\left(w_{,rr}+\frac{\nu }{r}{w}_{,r}\right)$ (8)

$\left(N_{\theta },M_{\theta }\right)=\left(A,B\right)\left[u_{,r}+\frac{\nu }{2}{w}_{,r}^2+\frac{u}{r}\right]-\left(B,D\right)\left(\nu w_{,rr}+\frac{1}{r}{w}_{,r}\right)$ (9)

其中A、B、D分别为拉伸、拉弯耦合和弯曲，刚度定义为

$\left(A,B,D\right)={\displaystyle {\int }_{-h/2}^{h/2}\left(1,\left(z-z_0\right),{\left(z-z_0\right)}^2\right)}\frac{E\left(z\right)}{1-{\nu }^2}\text{d}z$ (10)

2.2. 控制微分方程

Pastrnak模型的压力–位移关系假定为

$p=k_{w}w-k_p{w}^{″}$ (11)

这里 $k_w$ 是地基弹性模量， $k_p$ 是地基剪切模量。

弹性地基上圆板静力平衡方程如下 [16]

$N_r-N_{\theta }+r{N}_{r,r}=0$ (12)

$M_{r,rr}^2+2M_{r,r}/r-M_{\theta ,r}/r+{\left(r{N}_r{w}_{,r}\right)}_{,r}/r+k_{w}w+k_p\left(w_{,rr}+w_{,r}/r\right)=q$ (13)

将式(5)~(8)代入方程(12)和(13)，整理后可获得位移形式的基本控制方程，然后再引入如下无量纲变换

$\left(X,W\right)=\left(r,w\right)/a$， $U=\frac{ua}{h^2}$， $\eta =\frac{a}{h}$， $F_1=\frac{B}{D}h$， $F_2=\frac{A}{D}{h}^2$， $F_3=\frac{B}{Ah}$，

$\left(K_w,K_p\right)=\left(k_w{b}^4,k_p{b}^2\right)/D$， $Q=\frac{a^4}{Dh}q$ (14)

得到无量纲控制方程表示如下：

$U_{,XX}+U_{,X}/X-U_{,X}/X^2+W_{,X}{W}_{,XX}+\left(1-\nu \right)W_{,X}^2/2X=F_3{W}_{,XXX}+W_{,XX}/X-W_{,X}/X^2$ (15)

$\begin{array}{l}{W}_{,XXXX}+2W_{,XXX}/X-W_{,XX}/X^2+W_{,XXX}/X^3\\ =F_2(\nu U_{,X}{W}_{,X}/X+\nu W_{,X}^3/2/X+U{W}_{,X}/X^2\\ +\left(U_{,X}{W}_{,XX}+W_{,X}^2{W}_{,XX}/2+\nu U{W}_{,XX}/X\right)/\left(1-F_{1}F\right)\\ -F_1\left(W_{,XX}^2+W_{,X}^2/X^2+2\nu W_{,X}{W}_{,XX}/X\right)/\left(1-F_1{F}_3\right)\\ +\left\{K_{w}W-K_p\left(W_{,X}/X+W_{,XX}\right)+Q\right\}/\left(1-F_1{F}_3\right)\end{array}$ (16)

无量纲边界条件为：

$X=0$ 处， $W=finite$， $U=0$， $W_{,X}=0$， $\underset{X\to 0}{\lim }\left(W_{,XXXX}+W_{,XX}/X\right)=0$ (17a)

$X=1$ 处， $W=0$， $U=0$， $W_{,X}=0$ (17b)

3. 数值结果和讨论

分析中考虑由铝(Al)和氧化锆(ZrO₂)复合而成的FGM圆板，其弹性模量分别为 $E_m=70GPa$， $E_c=151GPa$，泊松比均为 ${\nu }_i\left(i=c,m\right)=0.3$。当 $\left(K_w,K_p\right)=\left(50,10\right)$ 时，为Pasternak地基支撑圆板，当 $\left(K_w,K_p\right)=\left(50,0\right)$ 时，退化为Winkler地基支撑，当 $\left(K_w,K_p\right)=\left(0,0\right)$ 时，退化为无地基支撑。首先，给定梯度指数为 $p=2$，图2考察了不同地基下圆板中心挠度随载荷的变化情况,显然，给定相同载荷下，Pasternak地基上FGM圆板的变形最小，无地基支撑圆板的最大，Winkler地基上FGM圆板的变形介于Pasternak地基和无地基之间。三种情况下FGM圆板的变形随横向载荷的关系均为非线性递增。

Figure 2. Q-W(0) curve under each foundation, p = 2

图2. 各地基下Q-W(0)关系曲线(p = 2)

下面考察Pasternak地基对FGM圆板弯曲行为的影响。给定 $p=2$， $K_p=5$， $K_w$ 取不同值时中心挠度即最大挠度如图3所示。不难看出，随着值的增加，板的变形减小，这相当于增加了板的约束，另外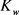，越大，变形随载荷的变化非线性程度有所削弱。说明地基弹性模量对FGM板的挠度有显著影响，而是地基剪切模量。

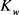图4为给定，，剪切模量取不同值时中心挠度随载荷变化的关系图。图中看出，越大，相同载荷下中心挠度越小。和图3相比较，不难发现对板变形的非线性性弱于对板变形的影响。

图5中给定了Pasternak地基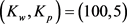，考察了梯度指数变化对FGM圆板弯曲行为的影响。图中看出，梯度指数越大，变形也随之增大，纯陶瓷板的变形最小，纯金属板的最大。说明随着FGM板中随着金属成分的增加，会削弱板的弯曲刚度。另外，该图中也增加了无地基FGM板的变形曲线，和有Pasternak地基相比，同样梯度下的FGM板的变形相比较会提高。

图6给出了不同地基下随梯度指数对FGM圆板最大挠度的影响。不出意外，随着p的增加，中心无量纲挠度也增加；随着弹性地基系数的增加，板的变形减小。和图4结论一致，p越大中心挠度越大；的增加会削弱p对板变形的非线性程度的影响。

Figure 3. The influence of K_w on Q-W(0) relationship

图3. K_w对Q-W(0)关系的影响

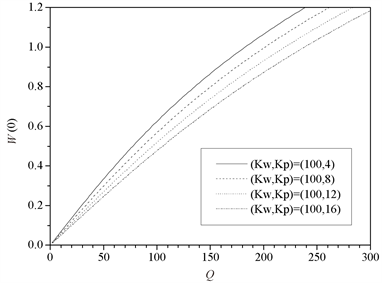
Figure 4. The influence of K_p on Q-W(0) relationship

图4. K_p对Q-W(0)关系的影响

Figure 5. Q-W(0) relationship of circular plates on Pasternak foundation under different gradients

图5. 不同梯度下Pasternak地基圆板Q-W(0)关系

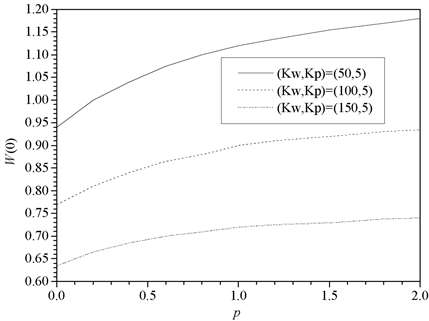
Figure 6. W(0)-p variation relationship under different foundations

图6. 不同地基下W(0)-p变化关系

4. 结论

引入物理中面的概念，消除了材料非均匀性导致的拉弯耦合效应，分析了Pasternak双参数弹性地基上FGM航空圆板非线性弯曲弯曲力学行为。数值计算结果表明：

(1) 材料梯度指数一定时，Pasternak地基下FGM板的变形小于相同工况下的Winkler地基板，板的挠度随载荷的增加非线性递增。

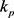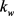(2) 相比地基剪切模量，地基弹性模量对FGM板的非线性弯曲影响更加显著，越大，变形的非线性程度越弱；当一定时，随着的增大，板的变形减小。

(3) 地基系数一定时，随着梯度指数的增加，板的变形也随之增加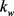；越大，变形的非线性程度越弱。

NOTES

^*通讯作者。