智能压实质量数值仿真研究

Research on Numerical Simulation of Intelligent Compaction Quality

摘要: 在道路路基压实过程中，随着压实的进行，土体力学参数实时发生变化，但目前的研究中仍假定其参数不变。针对这一问题，本文建立了压实度K与应变ε之间的关系，开展了室内试验并明确了压实度K与土体强度指标(粘聚力c、内摩擦角φ)间的关系，开发了ABAQUS有限元数值软件的子程序UMAT，实现了对路基土压实质量更为精确的计算，并与模型假定压实质量进行了比对分析，验证了路基土智能压实计算结果的精确性。在此基础上，进行压实程度影响因素(频率、激振力、自重)正交试验并进行敏感性分析。相关研究成果可为路基路面压实质量精确控制的相关研究提供指导和依据。

Abstract: In the compaction process of road subgrade, the mechanical parameters of soil change in real time with the compaction process, but the current research still assumes that the parameters remain unchanged. In order to solve this problem, this paper established the compaction degree of the relationship between K and the strain ε, carried out the indoor test and cleared the compaction soil K and the intensity index (cohesive force c, internal friction Angle φ), the relationship between development of the fem software ABAQUS UMAT subroutine, implemented the compaction of subgrade soil quality more accurate calculation, and comparative analysis, the model assumes that the compaction quality intelligent subgrade soil compaction was verified the accuracy of the calculation results. On this basis, orthogonal tests were carried out on the factors affecting the degree of compaction (frequency, excitation force, weight) and sensitivity analysis was carried out. The calculated results are more stable and accurate. The related research results can provide guidance and basis for the research of precise control of compaction quality of subgrade and pavement.

1. 绪论

近年来，我国不断加强道路基础设施建设，公路总里程数年年增加 [1]。据交通部数据预测，到2020年，我国公路总里程将达300万公里以上。然而与之相比，我国的机动车保有量更是呈现爆发式增长，这就导致了我国公路交通量日渐繁重，车辆负载不断增加，再加上公路运行时间的不断变长，导致公路在运营过程中沉陷、坑洼、水毁、开裂和车辙等破损现象屡见不鲜，严重影响了道路使用寿命与服务水平 [2] [3] [4] [5]。为了适应新的交通环境，提高路面服务质量与耐久性，广大学者对路基路面的压实质量控制提出了更高的要求。随着信息时代的带来，各个行业向着信息化、智能化的方向发展，道路行业也不例外。因此，智能压实技术应运而生，对于道路在智能压实施工下压实度的实时监测及反馈成为各国科研人员关注的重点。

1974年，瑞典公路协会的Dr. Heinz Thurner首次将加速度传感器安装到振动压路机进行现场试验。该现场试验是智能压实行业的一次革命 [6]。试验表明，压实力与一次谐波幅值与激励频率幅值之比有关。在同一时期，日本科学家Yoo和Selig就提出，随着土体被压实遍数不断增加，土体的刚度、阻尼及振动轮的竖向加速度也是在不断变化的。由此，将加速度的幅值作为判断压实度的指标 [7]。在21世纪初期，以瑞典为中心展开的研究 [8] [9] [10] 提出，通过对振动轮加速度信号的提取，进行傅里叶变换，然后以“谐波比HVR值”即二次谐波与基波幅值之比作为道路压实质量的控制指标 [6]。日本建设省土木研究所在“谐波比”法的基础上，进一步研究时发现，当土体被压实到一定程度后，“谐波比HVR值”会出现紊乱，这是由于土体刚度增大到一定程度后，会对振动轮提供一个反力 [11] [12] [13]。因此，岛津等人在此基础上提出，以振动轮加速度的二次以上所有的谐波幅值的平方和均方与基波幅值的比值，称之为“应变率”，作为评价压实质量的指标 [14]。

2007年，Rinehart和Mooney通过现场试验发现，土体刚度系数随着压实遍数的增大而增大，而振动轮垂直方向加速度的振动响应波形与激振波形的相位差角却相应地减小 [15]。因此提出了将振动轮的振动响应波形与激振波形的相位差角作为压实程度的评价指标 [7]。

2004年美国开始着手研究智能压实，美国联邦公路局公布了“FHWA智能压实战略计划” [16]。2012 年美国联邦公路(FHWA)局颁布了岩土填料及沥青混合料智能压实标准，并在2014年美国颁布国家智能压实标准，随后2016年美国半数州交通局颁布州立智能压实标准，同年，国家智能建设技术学会成立，解决了许多技术难题，其中包括根据振动压路机动态响应识别填筑体模量问题。目前，由于加速度信号易于获取，且可实现检测压实质量的连续性，使用最广泛的压实质量评价指标，基于加速度信号的“谐波比”法被广泛用于评定智能压实质量。此外，大多数学者开展数值计算中假定土体参数是固定不变的，这与实际工程存在一定的误差 [17]。

本文将通过理论推导、室内试验建立压实度K与土体应变值ε和力学参数c、φ间的关系，开发了UMAT子程序，实现了数值计算压实过程中土体力学参数的实时变化，分析了压实过程土体位移、压实度以及CMV值的动态响应规律，可为路基土智能压实提供理论借鉴和指导。同时通过数值仿真的方法，对影响压实质量的三个压路机输入因素(频率、振幅、自重)进行正交实验，并进行相应因素敏感性分析。得到了影响压实质量最为显著的因素，并为路基土智能压实压路机输入参数的调节提供参考。

2. 方法

为能够模拟道路在压实过程中力学参数实时变化的特征，本文基于理论推导以及室内试验建立了道路路基压实过程中压实度K与应变ε的关系，以及压实度K与粘聚力c、内摩擦角φ间的关系；开发了ABAQUS数值计算的子程序UMAT，实现了土体参数的动态变化；并对压路机工作时的输入参数，进行敏感性分析，得到了影响压实质量最显著的因素，并为实际工程提出指导意见。

2.1. 压实度K与应变ε关系

在智能压实过程中，压实度K会随着压实的进行不断增大。在数值仿真的过程中，需要定义一个中间“场变量”来建立应力或应变与被压实材料强度指标的关系。因此，本文通过建立数学模型的方法来建立压实度K与应变的关系。

在建立数学模型之前，做以下3点假设：

1) 假设土体在压实过程中发生微变形，应变与原模型尺寸(长、宽、高分别为x、y、z)相比很小，模型依然是长方体。

2) 假设土体在被压实过程中，x、y、z方向发生的应变分别为：ε₁、ε₂、ε₃。

3) 假设土体的初始压实度K = 0.8。

如图1所示，黑色为压实之前的模型，蓝色为压实过程中模型。

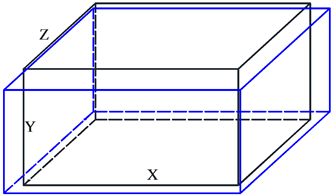
Figure 1. The model deforms at the beginning of compaction and during compaction

图1. 压实开始及过程中模型变形

根据以上三点假设，可以得到土体在压实过程中，所建立的模型体积V₁可由(1)计算得到：

$V_1=xyz\left(1+{\epsilon }_1\right)\left(1+{\epsilon }_2\right)\left(1+{\epsilon }_3\right)$ (1)

压实度K按(2)进行计算：

$K=\rho /{\rho }_{\max }$ (2)

密度ρ按(3)进行计算：

$\rho =m/v$ (3)

注：K为压实度

ρ为当前压实度K对应下的密度

ρ_max为最大干密度

m为密度ρ对应的质量

v为密度ρ对应的体积

在压实过程中，土体质量m不发生变化，且土体最大干密度ρ_max不变，只有体积v和密度ρ发生实时变化。由此可得：

$K=m/xyz\left(1+{\epsilon }_1\right)\left(1+{\epsilon }_2\right)\left(1+{\epsilon }_3\right){\rho }_{\max }$ (4)

且有：

${\rho }_{初始}=m/xyz$ (5)

将(4)、(5)联立，可得(6)：

$K={\rho }_{初始}/\left(1+{\epsilon }_1\right)\left(1+{\epsilon }_2\right)\left(1+{\epsilon }_3\right){\rho }_{\max }$ (6)

由假设3可知，模型初始压实度K_初始 = 0.8，带入(6)可得：

$K=0.8/\left(1+{\epsilon }_1\right)\left(1+{\epsilon }_2\right)\left(1+{\epsilon }_3\right)$ (7)

至此，通过数学建模的方法，确定的压实度K与应变ε之间的关系为：

$K=0.8/\left(1+{\epsilon }_1\right)\left(1+{\epsilon }_2\right)\left(1+{\epsilon }_3\right)$

通过建立中间“场变量”压实度K与应变ε的关系，实现了有限元数值仿真中实时获取压实度K。在下文中将建立压实度K与土体强度指标c、φ值的关系，进一步实现土体参数在压实过程中实时变化。

2.2. 压实度K与土体c、φ值之间的关系

本文开展了土体试件在不同压实度下的直剪试验，得到了不同压实度下土体的c、φ值，为下一步数值模拟提供土体力学参数；通过数据拟合明确了压实度与土体c、φ值间关系。

2.2.1. 试验方案

本文以黄泛区粉土为研究对象，开展了压实度分别为0.8、0.85、0.9、0.93、0.94、0.96、1的直剪试验。不同压实度的试件所需土体质量计算方法为：试验过程如图2所示。

$m={\rho }_{\text{dmax}}K\left(1+\omega \right)V$ (8)

式中：

m——不同压实度所需土的质量(g)；

ρ_dmax——土的最大干密度(g/cm³)；

K——压实度；

ω——含水率(%)；

V——静压桶体积(cm³)。

Figure 2. Direct shear test in room

图2. 室内直剪试验

2.2.2. 结果整理

不同压实度的直剪试验结果如图3所示：

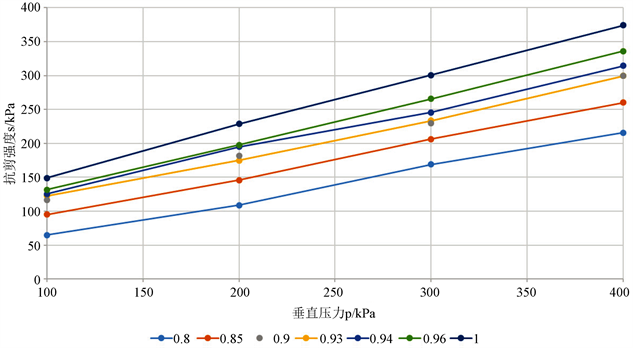
Figure 3. Curve of shear strength and vertical pressure

图3. 抗剪强度与垂直压力关系曲线

由图3的试验结果计算得到不同压实度下土体的c，φ值，如表1所示：

Table 1. Shear strength indices with different compactness

表1. 不同压实度的抗剪强度指标

根据试验结果拟合压实度K与粘聚力c、摩擦角φ的拟合结果如图4、图5所示：

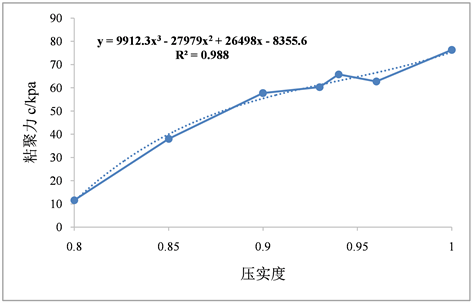
Figure 4. Compactness-cohesion curve

图4. 压实度–粘聚力关系曲线

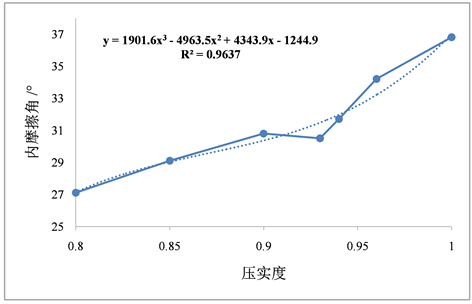
Figure 5. Compactness-friction Angle curve

图5. 压实度–摩擦角关系曲线

由图4可得到压实度与粘聚力c的关系为：

$y=9912.3x^3-27979x^2+26498x-8355.6$ (9)

由图5可得到压实度与摩擦角φ的关系为：

$y=1901.6x^3-4963.5x^2+4343.9x-1244.9$ (10)

2.3. 有限元数值仿真模型建立

本文采用ABAQUS有限元计算软件，添加压实度K作为基本场变量，编写子程序UMAT，实时读取模型体的ε₁、ε₂、ε₃，以压实度K为中间变量，可实现土体力学参数在压实过程中的动态变化。

由研究可知 [18]，压实过程中振动轮在水平向影响范围约为5 m。因此，数值模型的长、宽分别为10 m。在实际施工过程中，松铺厚度为20~30 cm，本文取30 cm，下层地基取3.7 m。在边界条件方面，由于模型尺寸足够大，不存在尺寸效应对仿真结果造成影响，因此四个侧面以及底面设置为固定约束。根据压路机振动轮的宽度为2.1 m，振动轮在前进方向与压路机的接地宽度为20 cm~30 cm，本文取25 cm，因此施加荷载为一个周期循环的面荷载。面荷载由两部分组成，第一部分为压路机的自重，第二部分为激振力。根据下表2实际振动压路机的参数，压路机自重所带来的面荷载大小为：(3000 + 2600)/(0.25*2.1) = 10.7 kPa。同理，激振力所带来的面荷载大小为11.4 kPa，且振动压路机的角速度为219.8 rad/s，近似取220 rad/s。因此，施加的周期面荷载为：P = 11.4 + 10.7sin220t (kPa)。

Table 2. Parameters of roller

表2. 压路机的基本参数

被压实土体的参数见表3。

Table 3. Mechanical parameters of soil

表3. 土体力学参数

建立的数值模型如图6所示。

Figure 6. Numerical model diagram

图6. 数值模型示意图

2.4. 基于有限元数值仿真的正交试验

在此前，本文已完成有限元数值仿真子程序的编写，实现了道路压实过程中，被压实材料强度指标的动态变化。由于每一个数值仿真工况所需时间较长，同时为了研究压路机的不同输入参数对压实质量的影响。本节在此基础上，通过设计三因素三水平的正交试验的方法，来探求各因素对压实程度的影响程度。由于选取的压路机输入参数有3个因素，每个因素有3个不同的变量。因此，全部工况有3³ = 27组，通过正交试验的方法，只需要进行9组工况的计算即可，很大程度上提高了计算效率。

频率、振幅、压路机自重是上文数值仿真中，组成所输入面荷载的三个因素。因此本文选取的三因素分别为：频率、振幅、压路机自重。每个因素对应3个水平，水平1与水平3为大多数压路机输入参数的最大值与最小值，水平2则采用内插法，进行选取。从而，建立的三因素三水平的正交试验工况表，如下表4所示：

Table 4. 3 factors and 3 levels orthogonal test table

表4. 三因素三水平正交试验表

通过表4正交试验表，可得到正交试验的9组工况中各因素对应的水平值选取，如下表5所示：

Table 5. Orthogonal test conditions

表5. 正交试验试验工况

3. 结果和分析

基于上述数值计算，得到了压实过程中土体的动力学响应，提取并分析了土体位移响应、压实度以及CMV值变化规律。

3.1. 压实过程的位移响应分析

被压实土体的位移响应如图7所示。

由图7可得：

1) 在压实初期，位移有一段快速变化的过程，约1 cm。这是由于压路机与土体接触的瞬间，由于压路机自身的重力，使得被压实材料产生快速沉降变形，这一部分变形即为静压压实深度。

2) 在振动压实过程中(0~3 s)，被压实材料的竖向位移曲线较为均匀的变化。总体来看，竖向位移曲线呈内凹形，即竖向位移绝对值增大的速率是在逐渐减缓的。在3 s时，被压实材料的沉降越为5.5 cm。也就是说，在前3 s完成了90%以上材料的压实。

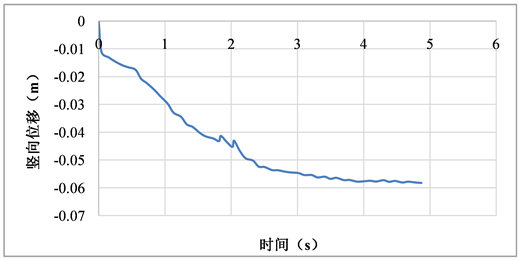
Figure 7. Displacement response diagram of compacted soil

图7. 被压实土体位移响应图

3) 竖向沉降量在3 s后，趋于平稳至5.9 cm，即5.9 cm为土体的最终沉降。此外，在本模型的松铺系数为0.2，土体厚度为30 cm，预计沉降量为：30 cm*0.2 = 6 cm，与数值计算结果5.9 cm相近，可知数值计算的竖向沉降量是合理的。

3.2. 压实过程中压实度K变化规律分析

由于道路可以看作一个半无限空间体，在振动压实的作用下，其水平面上(XOY)的位移变化很小，可忽略不计。因此将其竖向位移U₃的变化来表征压实度。

压实度K可按下式进行计算：

$K=\rho /{\rho }_{\max }$ (11)

其中，ρ = m/v，ρ_max = m/v_min，因此，压实度K同样可以按照下式计算：

$K=v_{\min }/v$ (12)

将模型看成一个半无限空间体，于是x，y不变。因此，压实度K可由竖向位移U₃表征出来：

$K=U_{3\min }/U_3$ (13)

其中：

v_min——达到最大压实度时的体积；

v——压实过程中实时的体积。

由(13)可得压实度与时间的关系曲线，如图8所示。

通过二阶高斯拟合，可得到在5 s内，压实度随时间变化的规律为：

$K=1.011{\text{e}}^{-{\left(\frac{t-1.337}{33.76}\right)}^2}-0.2867{\text{e}}^{-{\left(\frac{t+2.018}{3.093}\right)}^2}$ (14)

且相关系数R² = 0.9911。

从压实度K与时间的关系曲线中可以看出：

1) 压实度K随着压实的进行逐渐增大，在0~3 s中，压实度K从0.8逐渐增大到0.98，并趋于稳定。0~3 s中，在压实度K增大的过程中，压实度曲线呈外凸形状，其切线斜率逐渐减小，即压实度K增大速度逐渐降低。

2) 在压实进行到3 s以后，压实度K的变化趋于平稳，从0.98缓慢增长到1，说明被压实材料也已经趋于密实状态，接近其最大干密度。

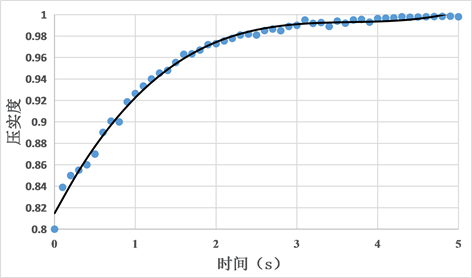
Figure 8. Curve of compactness K and time

图8. 压实度K与时间关系曲线

3.3. 压实质量评价指标分析

CMV值基于振动轮竖向加速度，考虑了振动轮直径、重量、频率、振幅等影响压实质量的因素，是一个常用的路基路面压实质量的评价指标。其计算公式如下：

$CMV=C\frac{A_{2\Omega }}{A_{\Omega }}$ (15)

式中：

$A_{\Omega }$ ：振动轮加速度振动波中基频的幅值；

$A_{2\Omega }$ ：振动轮加速度振动波中二次谐波分量的幅值；

$C$ ：常量系数。

由沉降分析可以看出，土体在0~3 s沉降变化最为显著。CMV与沉降同样可以反映路基的压实质量，此外，CMV值的计算是基于一定数量的数据的基础上。若数据量过少，则CMV值计算不准确；若数据量过多，则CMV值对应的时域分段区间会变少，导致CMV值的数量减少，增大了分析结果的不稳定性。因此，综合以上两点，本文对CMV值的计算分析取0~3 s，每0.5 s计算一次CMV值，共计算6次CMV值。

在数值计算过程中对加速度信号进行提取，通过MATLAB中离散傅里叶(FFT)变换，将时域信号转换成频域信号，并按照(14)计算得到CMV值，如图9所示。

Figure 9. CMV value at 0~3 s stage

图9. 0~3 s阶段CMV值

Figure 10. CMV curve over time

图10. CMV值随时间变化曲线

由图10的CMV值变化曲线可知：

1) CMV为非恒定值，并在一定范围内发生波动，这一现象与现有大量现场试验以及文献中的结果较吻合。

2) 在0~3 s范围内CMV值变化曲线呈“M”型，第二个波峰高于第一个波峰，这与“随着压实程度的提高，CMV值逐渐增大”的结论较为一致。

3) CMV值是一个可定性分析压实程度的压实质量评价指标，却不能用作一个定量的压实质量评价指标。这是由于在压实质量达到一定程度之后，被压实材料会压路机的抗力会增大，产生高次谐波，导致CMV值的精确度降低。

3.4. 压实程度影响因素敏感性分析

通过有限元数值仿真的方法，可得到表5正交试验9组工况对应的加速度响应。这里选择1~5 s时间内CMV的平均值(每0.5 s计算一次CMV值)作为压实质量评价的指标。利用上文提到的离散傅里叶变换，可得到每组工况对应的CMV平均值，如下表6所示：

Table 6. CMV under various conditions of orthogonal test

表6. 正交试验各工况下CMV值

根据上表6的计算结果，采用极差分析法进行压实程度评价指标CMV值主控因素分析。分析过程如下：可假定m_ij为第i因素j水平所对应的计算指标总和， ${\bar{m}}_{ij}$ 为m_ij的平均值。 ${\bar{m}}_{ij}$ 的大小反映了第i因素对CMV值影响的大小， ${\bar{m}}_{ij}$ 的大小用极差R_i表示，即R_i = Max( ${\bar{m}}_{ij}$ ) − Min( ${\bar{m}}_{ij}$ )。R_i越大，说明该因素对CMV值的影响也越大，Max(Ri)对应的因素是最主要的因素，Min(R_i)对应的因素为所有因素中影响最小的因素。正交试验极差分析结果如下表7所示：

Table 7. Range analysis table of orthogonal test

表7. 正交试验极差分析表

由极差分析表的结果可以看出：

1) 频率、振幅、自重的极差值逐渐减小，各因素按照该顺序对压实程度评价指标CMV值的影响依次减小。

2) 频率和振幅的极差值远远大于自重的极差值，说明频率以及振幅对CMV值的影响十分明显。

不同因素对CMV值的影响趋势如下图11所示。

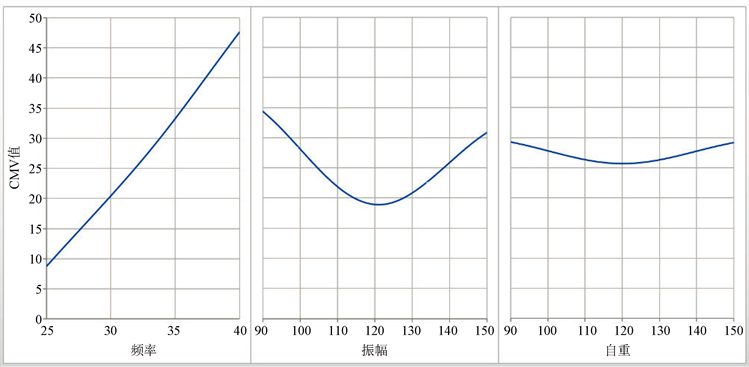
Figure 11. The influence trend of different factors on CMV

图11. 不同因素对CMV值的影响趋势

从上图中可以看出：

1) 在压路机的工作范围之内，频率是对压实质量影响最为显著的因素。不难看出，在压路机工作频率范围内，压实质量与频率呈正相关系，即压实质量随频率增大而增大，随频率减小而减小。

2) 在压路机的工作范围之内，作为影响压实质量的因素，频率比自重的影响更为显著。与此同时，振幅与频率对压实质量的响应不是简单的线性关系，而是压实质量随着振幅或频率的增大，呈现先减小后增大的趋势。

3) 在压路机的工作范围之内，若要增大或减小压实质量，最有效的办法就是调整压路机的频率，调整压路机的频率也是最为便捷的方法。

4. 结论

本文基于智能压实过程中土体力学参数发生实时变化，开展了智能压实数值计算，得到了以下结论：

1) 通过理论推导、室内试验建立了压实度K与应变值ε和土体强度指标c、φ的关系，得到了土体强度指标在压实过程中的实时变化。

2) 数值计算结果可得：在压实初期位移快速增加，压实过程中位移变化较为均匀，并逐渐趋于平稳至5.9 cm，结果与试验假设结果值6 cm较为接近，验证了数值结果的正确性。