1. 引言
乡村企业是乡村产业发展的主导力量,对带动农民就业增收、推进农业农村现代化具有重要的意义和作用。当前我国乡村企业呈现出数量多、门类广的特点,涉及到农产品加工、仓储物流、直销直供、电子商务、休闲农业和乡村旅游等诸多方面,同时也面临着一些问题,主要是人才资源匮乏,贷款融资不足和用地环境受限等方面。在新时代乡村振兴战略的背景下,国家大力号召优秀人才入乡创业就业,为乡村企业的发展注入新鲜的血液,激发了农村产业的活力,同时还鼓励地方政府出台有效的政策,为乡村企业的发展提供可靠的帮扶,助力乡村企业实现现代化发展。但是由于乡村基础设施建设不足,优秀人才入乡大力性不高等原因,这一目标的实现仍然存在一定的困难。
目前已有学者对乡村企业发展进行了探讨和研究。袁枫朝 [1] 等建立了集体建设用地流转的三方博弈模型,分析了其中关键所在,为集体建设用地流转制度的创新提供了借鉴。汤文华 [2] 等对江西赣州培育发展农业龙头企业的状况进行了调研,分析了赣州农业龙头企业在发展过程中所面临的主要困难和问题,并给出了相应的对策和建议。王胜 [3] 认为建立健全的政策体系和营造良好的企业环境有助于农村企业对人才的吸引和培养。张煜萌 [4] 运用多元统计方法,分析了2014~2018年沪深市场上14家A股农业上市公司的具体数据,检验政府支持、研发投入与创新速度之间的影响机制,得出政府加大对农业企业的支持力度,农业企业增加研发投入,提升企业的竞争力,可实现创新发展。李青阳 [5] 等调研分析了湖南省农业小微企业现状:融资贷款难、国家政策扶持力度不够仍然是湖南农业小微企业面临的两大困境,并提出了有效的策略。高松 [6] 认为人才引进难、产品销售渠道建设难是影响乡村企业发展的主要因素,并提出了有效的解决方法。应海芬 [7] 对我国以农业龙头企业、家庭农场等为主的新型农业经济体进行研究,发现人才匮乏等问题阻碍着农业经营主体的产业化发展,并提出了相应的对策。从上述文献看出,人才引入困难是阻碍乡村企业可持续发展的一大关键因素。近年来演化博弈论迅速发展,涉及各个领域决策问题研究时取得了一定的成果,本文运用演化博弈理论 [8],对于乡村企业人才引入的问题建立地方政府、乡村企业和优秀人才三方博弈模型,分析了不同情形下各方的演化稳定策略,并通过数值仿真研究各个利益主体的决策交互行为,较为真实的展现了三方博弈行为的多样性和复杂性,从而有针对性的提出了推动乡村企业人才引入进而实现高质量发展的合理建议。
2. 模型构建与分析
假定三方有限理性的博弈群体分别是地方政府、乡村企业和优秀人才,构成一个动态演化系统,三方掌握有不完全对称的信息,均以自身利益最大化为目标,都具有不断学习,不断提高的能力。对于地方政府而言,有两个策略选择,分别是扶持和不扶持,扶持即对乡村企业和优秀人才提供资金支持,积极向外部人才市场推广地方乡村企业,组织引导双方参与人才交流会等;对于乡村企业而言,有两个策略选择,分别是大力引进人才和一般引入人才,大力引入人才即制定招聘计划,组织人资团队各地纳贤,为优秀人才提供良好的就业环境,给予优厚的待遇等;对于优秀人才而言,有两个策略选择,分别是乡企就业和城企就业。
假设1:乡村企业正常生产销售活动对当地经济的贡献为F;地方政府扶持时,乡村企业大力引入且优秀人才进入乡企,给当地创造的贡献增量为T1,而乡村企业一般引入且优秀人才进入乡企,给当地创造的贡献增量为T2;地方政府大力扶持时花费的成本为C0;地方政府参与扶持时,获得企业家、农民等其他力量认可带来的形象效用为P;地方政府扶持时,给大力引入的乡村企业提供的资金支持为S1,给选择进入乡企就业的优秀人才提供的奖励金为S2。在地方政府不扶持的情况下,乡村企业大力引入且优秀人才进入乡企对地方经济产生的外部效应为N1,乡村企业一般引入且优秀人才进入乡企对地方经济产生的外部效应为N2。
假设2:乡村企业正常生产销售活动自身获得的收益为Y;乡村企业大力引入时,地方政府扶持且优秀人才进入乡企产生的企业效益增量为O1,而地方政府不扶持且优秀人才进入乡企产生的企业效益增量为O2;地方政府选择扶持和不扶持时,乡村企业制定招聘计划和组织招聘工作所需付出的成本分别为为C1和C2;乡村企业大力引入时,为进入乡企的优秀人才提供的补贴为K;β表示在乡村企业一般引入时优秀人才的努力程度,其中0 < β < 1。
假设3:乡村企业大力引入时,优秀人才进入乡企就业所获得的基本薪酬为E0,乡村企业一般引入时,优秀人才进入乡企就业所获得的基本薪酬为E1;优秀人才在乡企就业是所需付出的劳动时间成本是C3;乡村企业一般引入时,优秀人才进入乡企为发挥岗位职能,自身额外所需花费的信息资源获取、知识技能学习的成本为t;优秀人才城企就业获得的收益为E2,所花费的成本为C4。
以上假设参数均大于零,且T1 > T2,O1 > O2,N1 > N2,O1 > O2,E0 > E1,C0 > P,E1 −C3 − t < E2 − E4。得到如表1所示支付矩阵:


Table 1. Payment matrix of local government, rural enterprises and talents
表1. 地方政府、乡村企业和优秀人才的支付矩阵
设地方政府采取“扶持”策略的概率是x,采取“不扶持”策略的概率是1 − x;乡村企业采取“大力引入”策略的概率是y,采取“一般引入”策略的概率是1 − y。优秀人才采取“乡企就业”策略的概率为z,采取“城企就业”策略的概率为1 − z。
2.1. 地方政府复制动态方程分析
令
是地方政府群体选择“扶持”策略的期望收益,
是地方政府群体选择“不扶持”策略的期望收益,
是地方政府群体的平均期望收益,则有:
由复制动态方程稳定性定理知:
1) 当
时,
,意味着对于所有的x都是稳定状态,即地方政
府无论选择何种概率的“扶持”策略均是演化稳定策略。
2) 当
时,有
,
,于是
是演化稳定
策略,即当乡村企业选择“大力引入”策略概率小于y*,地方政府最终会选择“不扶持”策略。
3) 当
时,有
,
,于是
是演化
稳定策略,即当乡村企业选择“大力引入”策略概率大于y*,地方政府最终会选择“扶持”策略。
由上分析可知,当地方政府花费的扶持成本减少,扶持时所产生的经济贡献增量增多,地方政府获得的形象效用提升,地方政府分别提供给乡村企业和优秀人才的扶持资金在合理范围内时,可以满足(3)条件,地方政府会由“不扶持”策略转向“扶持”策略。
2.2. 乡村企业复制动态方程分析
是乡村企业群体选择“大力引入”策略的期望收益,
是乡村企业群体选择“一般引入”策略的期望收益,
是乡村企业群体的平均期望收益,则有
由复制动态方程稳定性定理知:
1) 当
时,
,意味着对于所有的y都是稳定状
态,即乡村企业无论选择何种概率的“大力引入”策略都是演化稳定策略。
2) 当
时,有
,
,于
是
是演化稳定策略,即优秀人才选择“乡企就业”策略概率小于z*,乡村企业最终会选择“一般引入”策略。
3) 当
时,有
,
,
于是
是演化稳定策略,即当优秀人才选择“乡企就业”策略概率大于z*,乡村企业最终会选择“大力引入”策略。
由如上分析可知,当乡村企业大力引入时花费的成本减少,政府的资金支持增加,所提供给进入乡企的优秀人才补贴减少,大力引入情况下优秀人才进入乡企产生的企业效益增幅变大,可以满足(3)条件,乡村企业会由“一般引入”策略转向“大力引入”策略。
2.3. 优秀人才复制动态方程分析
令
是优秀人才群体选择“乡企就业”策略的期望收益,
是优秀人才群体选择“城企就业”策略的期望收益,
是优秀人才群体的平均期望收益,则有
由复制动态方程令稳定性定理知:
1) 当
时,
,意味着对于所有的z都是稳定
状态,即优秀人才无论选择何种比例的“乡企就业”策略都是演化稳定策略。
2) 当
时,有
,
,于是
是演化稳定策略,即地方政府选择“扶持”策略比例小于x*,优秀人才最终会选择“城企就业”策略。
3) 当
时,有
,
,于
是
是演化稳定策略,即地方政府选择“扶持”策略比例大于x*,优秀人才最终会选择“乡企就业”策略。
由如上分析可知,当优秀人才乡企就业获得的薪酬增加,获得地方政府的奖励金增多,乡村企业给予的补贴提高,在城企就业获得的整体收益减少时,可以满足(3)的条件,优秀人才会由“城企就业”策略转向“乡企就业”策略。
2.4. 三方演化策略分析
根据如上计算可以可将3个复制动态方程组成一个动态系统,并令F(x) = 0,G(y) = 0,H(z)=0,计算出该动态系统存在多个平衡点,根据Ritzberger和Weibull的研究 [9],主要讨论(0, 0, 0),(1, 0, 0),(0, 1, 0),(0, 0, 1),(1, 1, 0),(1, 0, 1),(0, 1, 1),(1, 1, 1)这八个点的渐进稳定性,其他的平衡点均是非渐近稳定点。基于Friedeman的结论 [10],可以通过雅克比矩阵分析微分方程的稳定性,进一步考虑该动态系统的雅可比矩阵为:
由李雅普诺夫第一法则 [11] 知,若平衡点为演化稳定点,则其所对应的雅克比矩阵的特征根λ1、λ2、λ3的实部小于零,对动态系统的平衡点进行稳定性分析,如表2所示(其中N表示正负性不确定的情况):


Table 2. Stability analysis of equilibrium point
表2. 平衡点稳定性分析
综上分析可知,平衡点(0, 0, 0)始终是演化稳定点,即地方政府不扶持、乡村企业一般引入和优秀人才城企就业,这是一种政策无效的演化状态,不能最终实现乡村企业引入优秀人才,阻碍了农业农村事业的现代化发展。这种情形产生的原因是地方政府去参与促成乡村企业主动引入优秀人才要花费的成本巨大,而不去主动扶持;乡村企业缺乏长远的规划,不积极参与纳贤,使得优秀人才不愿在乡企就业;经济发达城市创就业有更广阔的发展平台,优秀人才群体选择城企就业可以获得更多收益。
当满足条件
,
,
时,平衡点(1, 0, 1)是演化稳定点,即地方政府选择扶持、乡村企业一般引入和优秀人才进入乡企就业,这种情况下虽然乡村企业没有选择大力引入的策略,但是其他两方的大力参与,一定程度上推进了乡村企业的发展,使各方利益有所增加,但是缺乏乡村企业的协同,就不能使优秀人才充分发挥自己的才能,而且现有的乡企待遇条件,会挫伤他们的进取心,不努力去为企业创造更多的价值,不会全身心投入到企业的现代化建设中去。这种稳定状态虽然有积极作用,但并不是最理想的。
当满足条件
,
,
时,平衡点(0, 1, 1)是演化稳定点,即地方政府选择不扶持、乡村企业大力引入和优秀人才进入乡企就业,这种情况下乡村企业为优秀人才创造了良好的就业条件,优秀人才也入职乡村企业,双方协同合作一定程度上给农村产业的发展起到了促进作用,也对当地经济产生溢出效应。但缺少地方政府的扶持,很多优质的乡村资源不能得到充分的开发和利用,同时拥有优秀人才的乡村企业发展仍面临着土地和融资问题的巨大考验,而且后期会加重企业的成本负担,显然这种稳定状态不是最佳的。
当满足条件
,
,
时,平衡点(1, 1, 1)是演化稳定点,即地方政府选择扶持、乡村企业大力引入和优秀人才进入乡企就业,这种情况下三方共同协作,符合当下新时代乡村振兴战略的指挥方针,地方政府积极解决乡村企业人才匮乏的问题,提供发展机遇,乡村企业也主动营造良好的就业环境,吸引人才入职,同时优秀人才响应政策号召,进入乡企创造价值,这种良性循环使得各方的收益都达到最大,是一种最理想的稳定状态,符合新时代现代化发展的要求,应该努力促成这种稳定状态的实现。对于三方利益相关者而言,具体最终演化稳定策略受各种因素的影响,下面通过数值模拟仿真来直观地展示策略动态演变过程。
3. 数值模拟仿真
3.1. 三方策略动态演化过程
主要考虑能够演化到最理想的稳定状态的情形,不妨假设各参数值:T1 = 8,P = 2,C0 = 3,Q = 2,O1 = 6,K = 2,E0 = 3,C3 = 2,E2 = 4,E1 = 2,C4 = 3,T2 = 6,N1 = 3,N2 = 2,t = 2,O2 = 4,C2 = 5,C1 = 1,S1 = 1.5,S2 = 1,β = 0.5。在这种假设条件下,首先对三方的策略选择行为进行演化仿真如图1所示,不论初始状态在何位置,整个动态系统会向着两个渐进稳定点(0, 0, 0)和(1, 1, 1)演化并最终达到稳定状态,这也印证了如上均衡分析所得到的结果。
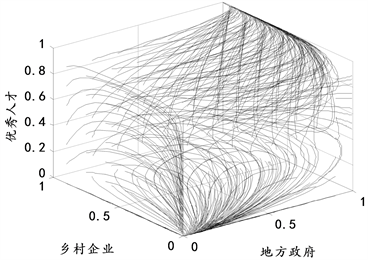
Figure 1. Evolution process of tripartite stakeholder strategy
图1. 三方利益相关者策略演化过程
3.2. 部分相关参数变化对三方策略选择影响的数值仿真
双方初始策略选择概率x = 0.5,y = 0.5,z = 0.5;采用控制变量的方法,保持其他的参数与初始设置一致,使得其中的一个参数在一定范围内变化,然后进行数值模拟仿真,观察三方演化稳定策略的变化。
地方政府给予乡村企业的资金支持S1变化对各方最终策略选择的影响。保持其他的参数不变,使S1在一定范围内变化,多次演化模拟仿真得到图2所示的模拟仿真图。可以看出当S1设置较小时,乡村企业选择一般引入,优秀人才选择城企就业,地方政府也由于二者的不大力协同,最终趋向于“不扶持”策略;随着S1的不断增大,乡村企业和优秀人才因为期望收益的增加,开始转变策略,地方政府也因为二者的参与,改变策略向着“扶持”方向演化。

Figure 2. The influence of cost subsidy change on the choice of tripartite strateg
图2. 成本补助变化对三方策略选择影响
地方政府扶持成本C0对各方最终策略选择的影响。保持其他的参数不变,使C0在一定范围内变化,多次演化模拟仿真得到如图3所示的模拟仿真图。可以看出一开始在C0较小的情况下,地方政府会大力选择扶持策略,乡村企业会选择大力引入策略,优秀人才选择乡企就业策略,但随着C0的不断增大,地方政府会开始向着不扶持策略开始转变,这时其他两个参与方也会在权衡自身利益后,不会主动去参与到其中,分别向着一般引入、城企就业开始转变,最终达到政策无效状态。

Figure 3. The influence of support cost change on the choice of tripartite strategy
图3. 扶持成本变化对三方策略选择影响
乡村企业大力引入时优秀人才乡企就业的基本薪酬E0对各方最终策略选择的影响。保持其他的参数不变,使E0在一定范围内变化,多次演化模拟仿真得到图4所示的模拟仿真图。可以看出当E0在一个较低的水平时,优秀人才选择城企就业,地方政府会选择不扶持,乡村企业会选择一般引入策略。随着E0不断增大,优秀人才在“乡企就业”策略下所获得的整体期望收益增大,率先做出改变选择乡企就业,之后乡村企业也改变策略选择大力引入,地方政府也改变策略选择扶持。

Figure 4. The influence of basic salary change on the choice of tripartite strateg
图4. 基本薪酬变化对三方策略选择影响
4. 结论与建议
本文结合实际情况,运用演化博弈理论建立了地方政府、乡村企业和优秀人才的三方博弈模型,分析了各利益相关者之间的决策行为的演化路径,并得出了在不同参数条件下的演化稳定状态,所有可能的稳定策略有(不扶持,一般引入,城企就业),(扶持,一般引入,乡企就业),(不扶持,大力引入,乡企就业),(扶持,大力引入,乡企就业)。针对最理想的演化稳定状态(扶持,大力引入,乡企就业),通过数值仿真直观地展示了整个系统的演化过程,以及参数变化对策略选择的演化路径的影响。综合上述分析结果提出如下建议:
乡村企业的发展有利于带动农村农民脱贫致富,进而推进农业现代化的实现,对地方政府而言,要有长远的目光看待乡村企业的未来发展,积极引导优秀人才进入乡村企业,建立健全的乡村企业人才引入的扶持机制,这样既有机会减少地方政府扶持的运作成本,又能充分地满足乡村企业和优秀人才的需求,让他们主动参与其中。同时地方政府还要解决优秀人才工作之外时所面临的困难,精准施策,提供帮助。
乡村振兴战略的实施为农业农村事业实现高质量发展带来了机遇,乡村企业应该制定适时的企业发展战略,不应被动和保守,积极主动吸纳优秀人才资源,与地方政府通力合作才是长久之计。优秀人才具备现代化管理手段和技术,进入乡村企业工作有利于充分发倔农村产业特色优势,农村优质的农产品以及自然资源等得到了有效配置和利用。同时面对的新生代的人才资源,乡村企业要提供合理的帮助,充分调动他们的积极性,使他们努力投身到企业建设和发展中去。
当今社会城市人才资源趋于饱和状态,而农村人才资源却相对匮乏,使得乡村企业始终得不到更长远的发展,作为新时代的知识型和技能型的人才应该有责任去参与到乡村企业的发展和建设当中去,克服困难,为农业农村信息化和现代化增添动力,进一步助力三农事业发展。同样乡村振兴战略背景下,对他们也是巨大的机遇,要认识到农业在我国新时代发展中的重要地位,进入乡企就业在实现个人价值的同时实现了社会价值。
基金项目
国家自然科学基金资助项目(No. 12061065)。