基于R软件的数理统计可视化教学研究——以最大似然估计为例

Research on Visualization Teaching in Mathematical Statistics Basing on R Software—Taking the Maximum Likelihood Estimation as an Example

摘要: 在数理统计课程的教学过程中，利用R软件实现可视化教学，帮助学生建立统计思维.本文以最大似然估计教学内容为例，通过R软件绘制对数似然函数的图像，似然估计的相合性与正态渐近性等可视化教学示例，可以直观地解释似然函数的意义，理解最大似然估计的统计性质。结果表明，可视化教学能够使学生更加深刻快速地掌握数理统计的理论方法，提高学生学习效率。

Abstract: In the teaching process of mathematical statistics course, R software is used to realize visualization teaching and help students to establish statistical thinking. Taking the teaching content of maximum likelihood estimation as an example, this paper uses R software to draw the image of the log-likelihood function, and visualization teaching examples of the consistency and asymptotic normality of likelihood estimation, so as to intuitively explain the meaning of likelihood function and understand the statistical properties of maximum likelihood estimation. The results show that visualization teaching can help students to grasp the theoretical methods of mathematical statistics more deeply and quickly, and improve their learning efficiency.

1. 引言

数理统计是数学专业的基础必修课，如何培养学生建立统计思维方法，是本门课程的重要任务。统计思维方法主要体现在在不确定性现象中寻找统计规律性的东西，与一般的数学思想方法培养有明显不同。而数理统计所以难度大，恰在于其结果的不确定性，有些难以被学生直接感知，使得学生往往不知如何去意会。大部分学生，只知道计算方法，却不知道为什么要这样计算，也不能清晰解释计算结果的实际意义，更不具备统计思维能力。教师需要挖掘数理统计中的关键的概念与方法，建立“可见形式”与“不确定形式”之间的直接联系，使统计推断结果变得可见并且可操作，突破“意会”与“言传”间的交流障碍，为学生理解概念创设直观背景，启发学生解决问题探究规律的思路。

为了解事物之间的相互关系及发展趋势，通过可视化技术来进行表征是一种常用的方法。所谓可视化(Visualization)是指通过计算机软件的支持，将事物及其发展变化的形式和过程，用仿真化、形象化的方式表现出来，一般而言，包括数据、模型和过程三方面的可视化，从用户角度看可视化主要就是信息提供的可视化，也就是信息服务界面的可视化。可视化的目标是帮助人们增强认知能力，理解事物间的联系，降低认知的难度 [1]。

R软件 [2] 属于GNU系统的一个自由、免费、源代码开放的软件，它是一个用于统计计算和统计制图的优秀工具，而且R软件系统小，具有良好的统计图形界面，特别有利于数据模拟和数据的可视化，同时，数学计算功能也较强，适合于教学要求。

2. 可视化教学设计实例

最大似然估计是数理统计课程的教学重点内容。一般地，对于最大似然估计求解方法，学生往往只记住求解参数估计值的步骤以应对考试，却不理解最大似然估计的基本原理和统计性质。针对学生难以理解的内容和出现的问题，进行可视化教学设计。

2.1. 似然函数与对数似然函数的比较

根据最大似然估计原理，即求解使得出现该试验结果概率最大的参数值。一般地，总体的概率分布函数形式都比较复杂，所以，似然函数的表达式也都为复杂的乘积形式。由于函数与其对数函数在相同点处取得极值，因此，利用对数后求导的方法求解，得到参数的最大似然估计。事实上，对数似然函数是凹函数，函数曲线具有明显的凹的特性。

下面以0-1分布为例

设随机变量X服从0-1分布，概率分布律为

$P\left(X=x\right)=p^x{\left(1-p\right)}^{1-x},x=0,1.$

$X_1,X_2,\cdots ,X_n$ 是总体X的样本， $\left\{x_1,x_2,\cdots ,x_n\right\}$ 为样本的一组观测值，则其似然函数为

$L\left(p;X_1=x_1,X_2=x_2,\cdots ,X_n=x_n\right)=p^{{\displaystyle {\sum }_{i=1}^n{x}_i}}{\left(1-p\right)}^{n-{\displaystyle {\sum }_{i=1}^n{x}_i}},0<p<1.$ (1)

对数似然函数为

$l\left(p\right)=\ln \left(L\left(p\right)\right)=\ln p{\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}+\ln \left(1-p\right)\left(n-{\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}\right).$ (2)

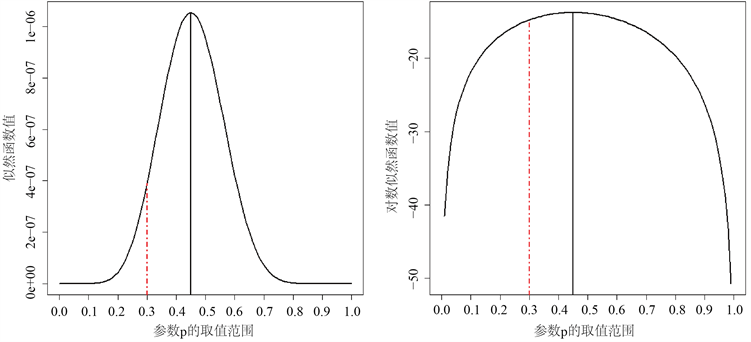
设0-1分布的参数 $p=0.3$，样本含量 $n=\text{2}0$，似然函数、对数似然函数的图像，以及最大似然估计见图1，其中图1(a)是似然函数式(1)的图像，图1(b)是对数似然函数式(2)的图像。

(a) 似然函数 (b) 对数似然函数

Figure 1. Graphs of the likelihood function and the log-likelihood function

图1. 似然函数和对数似然函数图像

参数的最大似然估计值 $\hat{p}=0.45$，可以看出，它在图1(a)和图1(b)中都是最大值点，但它不等于总体参数 $p=0.3$。似然函数和对数似然函数在0.3处也没有取得最大值。

另一方面，图1(a)是似然函数图像，函数曲线在参数取值范围 $\left(0,1\right)$ 内，只在区间 $\left(0.2,0.7\right)$ 内具有“凹”的特性，在其它取值范围内，函数图像曲线相对平缓，几乎平行于横坐标轴，不具有明显的“凹”的特性。图1(b)是对数似然函数图像，函数曲线在整个参数取值范围内具有明显的“凹”的特性。

2.2. 最大似然估计的相合性

最大似然估计的大样本性质如相合性和渐近正态性，即当样本含量n趋于无穷的过程中，最大似然估计量的变化趋势和极限分布。但学生在学习过程中对n逐渐趋于无穷时会出现什么样的情况无法想象，难以理解。因此，利用图像让学生进一步感受其性质蕴含的原理。

以0-1分布为例。从参数同为 $p=0.3$ 的0-1分布总体中分别抽取样本数 $n=20,50,100,200$ 的样本，利用0-1分布的对数似然公式(2)画出相应曲线，见图2。图中的虚线为0-1分布的参数真值，在上述样本含量下，得到参数的最大似然估计值分别为 ${\hat{p}}_1=0.15$， ${\hat{p}}_2=0.20$， ${\hat{p}}_3=0.26$ 和 ${\hat{p}}_4=0.29$，在图2中用实线标出。可以清晰的感受到，随着样本数n不断增加，估计值越来越接近参数真值 $p=0.3$。

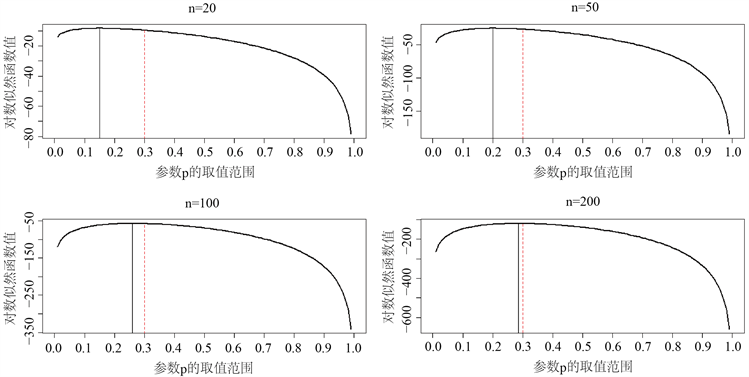
Figure 2. Maximum likelihood estimation results of 0-1 distribution parameters

图2. 0-1分布参数的最大似然估计结果

2.3. 最大似然估计的渐近正态性

事实上，最大似然估计量也是随机变量，也需要用概率分布描述它。

以0-1分布为例。试验也是在参数为 $p=0.3$ 的0-1分布总体中抽样，样本含量分别为n = 20，50，100，200，重复抽样1000次，得到1000个最大似然估计值 $\hat{p}$，画出在4种样本含量下 $\hat{p}$ 的频率直方图，如图3。由于0-1分布总体的二阶矩存在，满足博格中心极限定理的条件，因此， $\hat{p}$ 的极限分布为正态分布，即

$\sqrt{n}\left(\hat{p}-p\right)~N\left(0,p\left(1-p\right)\right).$

由图3，随着样本含量不断增加，最大似然估计量的分布也逐渐接近于正态分布。

2.4. 最大次序统计量的渐近分布

指数分布族包括如二项分布、指数分布等分布，指数分布族参数的最大似然估计具有较好的统计性质。为了与之区别，下面选择均匀分布，考察其参数的最大似然估计的统计性质。

设随机变量X服从均匀分布 $U\left(0,\theta \right)$， $\theta >0$，其概率密度函数为

Figure 3. Relative frequency histogram of maximum likelihood estimates for 0-1 distribution parameters

图3. 0-1分布参数的最大似然估计的频率直方图

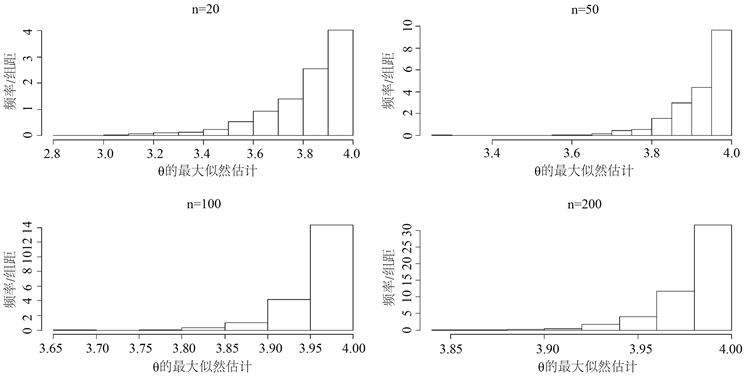
Figure 4. Frequency histogram of maximum likelihood estimation for uniformly distributed parameters

图4. 均匀分布参数最大似然估计的频数直方图

$f\left(x\right)=\{\begin{array}{l}\frac{1}{\theta },0<x<\theta ,\\ 0,其他\text{.}\end{array}$ (3)

$\left\{x_1,x_2,\cdots ,x_n\right\}$ 是从总体X中抽取的一组样本观测值，利用似然函数计算，它的最大似然估计为样本的最大次序统计量 $\hat{\theta }=x_{\left(n\right)}$，它具有相合性，但不具有渐近正态性。因为均匀分布 $U\left(0,\theta \right)$ 并不属于C-R正则族 [3]。

事实上， $\hat{\theta }=x_{\left(n\right)}$ 的渐近分布为Weibull类型的极值分布 [4]，其分布函数为

$H\left(x\right)=\{\begin{array}{l}\exp \left[-\left(\frac{\theta -x}{\theta }\right)\right],x\le \theta ,\\ 0,x>\theta .\end{array}$

有关渐近分布是极值分布的内容已经超出了本科教学范围，因此利用R语言对均匀分布重复抽样。从式(3)的均匀分布参数为 $\theta =4$ 的总体中抽取样本，样本含量分别为 $n=20,50,100,200$ 的样本，重复抽取1000次，各得到1000个 $x_{\left(20\right)},x_{\left(50\right)},x_{\left(100\right)}$ 和 $x_{\left(200\right)}$，分别画出它们的频数直方图，观察分布趋向极值分布的变化趋势。

由图4可以观察到，其渐近分布并不是正态分布，而是Weibull类型的极值分布。由于课程中不能向学生讲解极值分布的具体理论概念，因此利用图像直观的展示极值分布，使得学生更容易记忆理解。

3. 讨论

R软件是一个开放型软件，便于统计图形绘制，可将模拟结果与可视化教学相结合，直观呈现出比较抽象的概念，操作相对简便，适用于数理统计的教学需要。本文只是以最大似然估计为例，同样也能够推广到数理统计的其他教学内容，利用可视化表达方式，促进学生对数学概念和性质的理解，提高学生的学习积极性，提升教学质量，获得理想的教学效果。

基金项目

辽宁省科技厅引导项目(20180550196)。

NOTES

^*通讯作者。