基于PCA-LDA的非负光谱透过率生成方法

Deriving Nonnegative Spectral Transmittance Based on PCA-LDA

摘要: 本文针对高光谱成像，提出了一种基于主成分分析(Principal Component Analysis, PCA)和线性判别分析(Linear Discriminant Analysis, LDA)生成非负光谱透过率的方法。该非负光谱透过率可应用于可编程高光谱成像系统的光学成像结果等效于PCA-LDA数字模型后处理的高光谱数据的结果。该方法通过滤除训练过程中的负值，无需补偿透过比的二次采集，可以直接针对高光谱数据应用，即高光谱数据采集和PCA-LDA后处理可以通过光学成像的物理过程一次性同时实现，有助于在光学和遥感领域的信息应用中实现更智能便捷的光学检测与传感。

Abstract: In this paper, a method to derive nonnegative spectral transmittance based on Principal Compo-nent Analysis (PCA) and Linear Discriminant Analysis (LDA) is proposed for hyperspectral imaging. The nonnegative spectral transmittance can be applied to the optical imaging of programmable hyperspectral imaging system, and the collected images are supposed to be equivalent to the re-sults after PCA-LDA post-processing. By filtering out the negative value in the training process, the method can be directly applied to hyperspectral data, that is, hyperspectral data acquisition and PCA-LDA post-processing can be realized simultaneously through the physical process of optical imaging, which is helpful to realize more intelligent and convenient optical detection and sensing in sensing applications.

1. 引言

光谱分辨率在10⁻²λ数量级范围内的光谱图像称为高光谱图像，可以将图像与光谱信息结合。但是由于其信息量巨大，采集和数据处理速度十分缓慢。而可编程光学滤波器是一种用于处理高光谱信息的光学元件，可以通过调制空间光调制器 [1] 或数字微镜器件(DMD) [2]，将不同波长的光子多路复用到光电探测器上，其能够任意快速地切换其光谱透过率光谱。其灵活的光谱透过率直接实现了基于硬件的光谱数据后处理，根据光谱透过率对光谱数据后处理算法进行编码，在这种情况下，具有这种特定编码光谱透过率的光学测量可以等效于数值后处理后的高光谱数据的结果。与传统的基于扫描的高光谱遥感技术 [3] 相比，这种方法只需要采集一幅具有特定编码光谱透过率的图像，并且高光谱数据的采集和后处理可以通过快照光学成像的物理过程同时实现。这样，与基于扫描的高光谱遥感技术相比，数据采集和传输速度可显著提高至少数百倍，并且完全无需后处理。因此，可以克服高光谱遥感技术(例如，缓慢的数据采集 [4] [5]、海量数据传输和存储 [6] 以及计算费用高昂的后处理 [7] )的固有弱点，同时保留最关键的光谱信息用于光学检测和感测。近年来，人们对光谱透过率方面常用的光谱数据后处理算法进行了一些尝试，如偏最小二乘回归(PLS) [1]、基于巴氏距离的最大化正交二元滤波器 [8]、多元曲线分辨率(MCR) [9]，主成分分析(PCA)和线性判别分析(LDA) [10]、深度学习方法 [11]。但以往实验结果表明，上述方法生成的光谱透过率会在计算过程中产生负值权重 [10] [11]，而可编程滤光片在信息采集的时候只能使用正向的光谱透过率权重，因此针对负向的光谱段，需要反向采集光谱值，然后将正向采集的光谱透过率和反向采集的光谱透过率作差，从而生成新的透光率 [10]。两次采集会耗费更多时间和成本，无法在可编程滤光片中很方便的使用，对于日常应用仍有一定影响。因此，本文提出了一种基于非负PCA和LDA算法的应用于可编程光学滤波器的高光谱透过率方法，能够解决这种问题，并且对原本的光谱分类准确率影响极其微小。

2. 方法

如图1，本文使用的PCA-LDA模型由多个线性数据处理阶段组合构成。数据预处理阶段包括数据的格式调整和归一化处理；然后是PCA无监督降维，一般用于高维数据的降维，提取数据的主要特征分量；随后利用有监督的LDA方法进行分类，本文使用了高光谱数据集Salinas-A数据集进行编码光谱透过率的仿真模拟。

Figure 1. Data processing flow chart

图1. 数据处理流程图

本文使用的数据集是Salinas图像的一个小亚序列，即Salinas-A，也经常被使用。它包括86 × 83像素，位于同一场景内的[samples, lines] = [591-676, 158-240]，并且包括六个类 [12]。整体的多分类任务拆分策略：是使用了一对其余的思想，即分别把每类作为第1类，其余五类作为第2类，训练6个模型。由于可编程滤光片本质上是一个对于光向量的一维权重矩阵，因此我们只能采用线性的方法，训练得到一个权重系数矩阵。

2.1. 数据预处理

高光谱数据集SalinasA数据集是一个83 × 86 × 204的数据立方体，前两位体现了空间特征，而第三维是光谱维，主要体现光谱特征。首先为了计算方便，我们首先将数据进行变成799 × 204的二维信息，只保留光谱特征信息。第二步进行归一化处理，在编码光谱透过率光学成像的物理过程中，由于每个光谱的最大强度或所有强度之和都是未知的，因此不可能在物理过程中进行归一化。本文应用了一种基于全通滤波器的归一化方法 [11]，采用附加的全通滤波器(例如，每个波长的100%光谱透过率)并用这种全通滤波器捕获另一个光学图像，其中每个像素处获得的光学测量值应等于每个光谱在不同波长下的所有强度的总和。通过对编码光谱透过率光学测量和全通光谱透过率光学测量的划分，计算出归一化输出 $y$。由(6)可知，归一化输出 $y$。相当于归一化光谱通过编码透过比(即PCA-LDA后处理的归一化光谱)的结果，其中归一化光谱通过将每个波长的强度除以所有强度的总和来计算波长(公式(1)，其中 $s_{ij}$ 是每一条光向量 $s$ 的光谱强度，N是波长总数)。这样运算之后，将只保留波形特征，去除以幅度系数为主的线性特征，以保证阈值相对所有的光向量是公平的。

$x_i=t\cdot \frac{s}{{\displaystyle {\sum }_{j=1}^N{s}_{ij}}}$ (1)

2.2. 无监督PCA降维

这一步主要是对训练集所有数据计算PCA系数，并以最优主成分数进行降维，得到PCA系数矩阵A。这一步是无监督的，投影后的投影值可实现尽可能的分散，因为如果重叠就会有样本消失。可以从熵的角度进行理解，熵越大所含信息越多。具体的计算过程是，首先假设原始数据为 $n\times m$ 的矩阵X，将X的每一行进行零均值化，即减去这一行的均值。

$C=\frac{1}{m}X{X}^{\text{T}}$ (2)

通过式(2)求出协方差矩阵然后根据C，求出协方差矩阵的特征值及对应的特征向量。将特征向量按对应特征值大小从上到下按行排列成矩阵，取前k行组成矩阵P，即为降维到k维后的数据。而最终降维得到的矩阵，如式(3)所示，是特征矩阵和原矩阵的乘积。

$Y=PX$ (3)

我们将想要提取的光谱和其他光谱放到一个共同的矩阵里进行降维。最终我们根据选择能使误差小于0.01 (99%的信息都被保留)或0.05 (95%的信息都被保留)的k值。取系数矩阵P前8个降维后的向量，生成了新的维度为204 × 8的矩阵A，基本包含了所有的主要光谱信息，而其他未被取到的为极少量冗余信息。PCA算法通过舍去一部分信息之后能使得样本的采样密度增大，同时PCA不仅将数据压缩到低维，它也使得降维之后的数据各特征相互独立，这样更利于通过PCA提取分类特征。

2.3. 有监督LDA分类

正如前面所说，我们利用六次二分类，以达到多分类的目的，每一次我们将需要筛选的光谱设置为第一类，而其他所有的五类光谱设置为第二类。随后通过线性LDA对经过PCA降维后的结果进行线性分类处理，得到LDA系数矩阵B。具体的推导过程为，第一步计算类内散度矩阵 $S_w$，同时计算类间散度矩阵 $S_b$，然后计算矩阵 $S_w^{-1}{S}_b$ 以及 $S_w^{-1}{S}_b$ 的最大的d个特征值和对应的d个特征向量

$W=\left(w_1,w_2,\cdots ,w_d\right)$ (4)

对样本集中的每一个样本特征 $x_i$，转化为新的样本

$z=W^{\text{T}}x$ (5)

我们将维度为8 × 1的LDA权重系数矩阵 $W^{\text{T}}$ 记作B矩阵，最终我们期望的系数矩阵 $w$ 就是两个矩阵的乘积，即为式(6)。

$w=A\cdot B$ (6)

2.4. 去除负项权重

我们将得到的204 × 8维的PCA系数矩阵和8 × 1维的LDA系数矩阵相乘，求得维度为204 × 1的权重向量 $w=A\cdot B$ ；我们在这里利用LDA系数矩阵的翻转，得到了两个权重矩阵B和 $-B$，分别和A相乘得到 $w$ 和其负矩阵 $-w$。将 $w$ 和其负矩阵 $-w$ 进行比较，将 $w$ 和其负矩阵 $-w$ 进行比较，通过比较 $w$ 与 $-w$ 矩阵中负数项的数量，选择负数少的那一个，记为 $w^{\prime }$。随后通过公式(1)将 $w^{\prime }$ 中的负数置为０，实现了负数项个数的大幅减少。

$w_i=\{\begin{array}{l}0,w_i<0\\ w_i,w_i\ge 0\end{array}$ (7)

在实际应用中就相当于我们将光谱透过率为负权重的光向量进行屏蔽。这样，就得到了最终经过编码光谱透过率矩阵后的光向量结果，即线性模型公式(8)

$f\left(x\right)=w\cdot x$ (8)

2.5. 分类模型

根据我们的分类结果，利用ROC曲线和约登指数得到最佳分类阈值t。最终我们根据上述结果，得到了线性分类模型

$f\left(x\right)=\{\begin{array}{l}1,w\cdot x<t\\ 0,w\cdot x\ge t\end{array}$ (9)

我们通过阈值t，将目标光谱和其他光谱分成两类。针对6个类别中的每一个光谱我们都会有一个这样的光谱透过率模型，对应不同的波形和阈值，实际上是一个特征向量对矩阵做线性运算，然后根据阈值比较进行分类。

3. 结果

本文以SalinasA数据集为例，对所提出的智能高光谱遥感方法的全过程进行了数值模拟实验，使用了MATLAB R2018b进行了实现。为了合成可编程滤光片的编码透过光谱，通过PCA方法从6组光谱数据中获得前8个非负PCA向量，然后用LDA压缩到一维模型。通过筛选去除光谱透过率的负值再进行应用，得到最终的光谱透过率模型，通过图2我们可以看到编码后的光谱透过率模型没有负值，全都是正权重或零权重，而作为对比，使用传统PCA-LDA方法的光谱透过率波形为图3，我们看到里面会有很多负项的权重，需要二次采集补偿透过比。而使用了不含负项的PCA-LDA模型之后，这个编码光谱透过率的过程可以直接在可编程滤光片上实现，避免了在成像透过比之后采集补偿透过比的过程。

那么我们来看性能表现，如图4所示，我们可以看到所有的光谱都能被很好的分割，整体分类准确率(以6类光谱分割准确率的均值作为整体准确率)达到95%以上，和图5含负项的PCA-LDA光谱透过率分类结果进行对比，表现几乎完全一致。对比表1和表2可以看出，非负PCA-LDA方法所获得的光谱透过率在准确率等各项评价指标中表现未受影响，其中只有第12类光谱灵敏度下降了0.02%，可以忽略不计。

我们在使用传统含负数值的PCA-LDA分析的时候，我们统计光谱透过率系数矩阵的负项，发现针对第一到六类，传统算法的负数项相加多达616个，而通过表1和表2中负数项的对比我们可以看到，新算法通过对LDA系数的翻转，首先使得负数项大大降低，最终只有6个，然后置零，最终对性能指标基本没有影响。负数项个数少且幅值非常小，在光谱透过率图像中难以发现，因此这也是准确率基本不会改变的主要原因。但是相对于传统方法，避免了二次采集所需的时间和成本，收益远远大于损失。

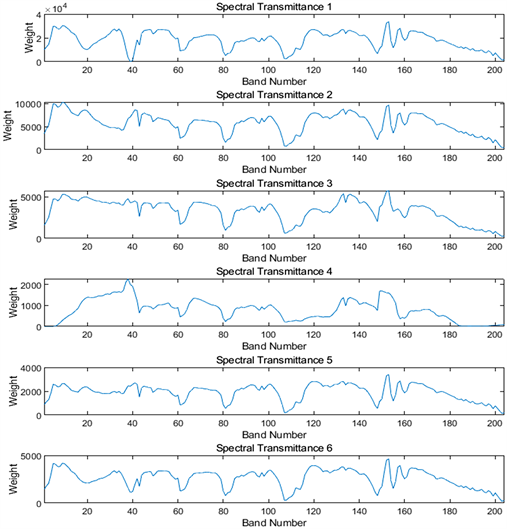
Figure 2. Spectral transmittance waveform of PCA-LDA without negative value

图2. 无负值的PCA-LDA光谱透过率波形

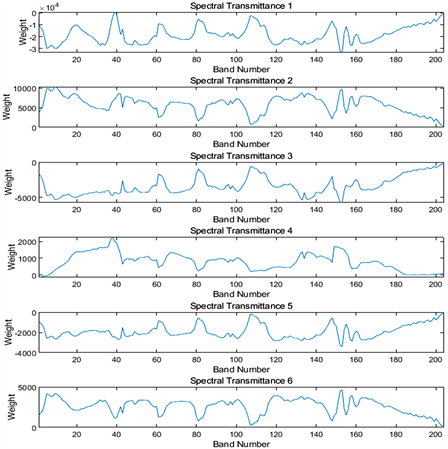
Figure 3. Spectral transmittance waveform of PCA-LDA with negative value

图3. 含负值的PCA-LDA光谱透过率波形

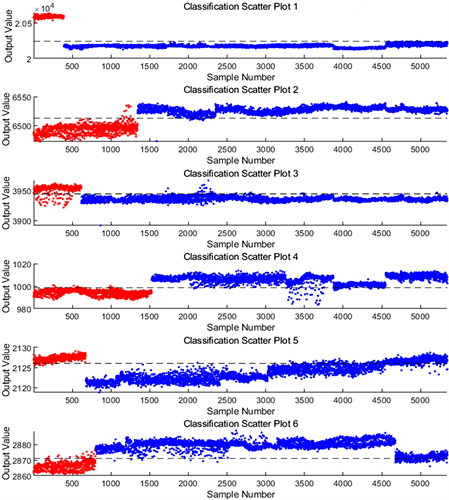
Figure 4. Classification results of PCA-LDA spectral transmittance without negative values

图4. 不含负值的PCA-LDA光谱透过率分类结果

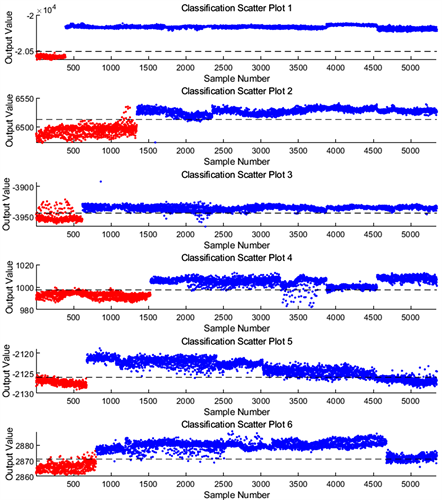
Figure 5. Classification results of PCA-LDA spectral transmittance with negative values

图5. 含负值的PCA-LDA光谱透过率分类结果

Table 1. Accuracy of PCA-LDA without negative values in Salinas a dataset

表1. SalinasA数据集不含负项PCA-LDA准确率

Table 2. Accuracy of PCA-LDA with negative values in Salinas a dataset

表2. SalinasA数据集含负项PCA-LDA准确率

对于传统的高光谱遥感技术，通常需要进行大量的扫描(如点扫描、线扫描或凝视)来获得完整的高光谱数据立方体，然后再进行大量耗费昂贵的计算进行后处理。相比之下，该方法根据光谱透过率对PCA-LDA进行编码，其中具有这种编码光谱透过率的光学图像可以等效为经过PCA-LDA后处理的高光谱图像的结果。因此，该方法无需扫描，只需采集具有特定编码光谱透过率的单个图像，其中高光谱数据采集和PCA-LDA后处理可以通过快照光学成像的物理过程同时实现。由于可编程光学滤波器可实现任意光谱透过率的超快调制速率 [10]，预计所提出的方法可将数据采集和传输速度提高至少数百倍于传统的高光谱遥感技术。

4. 结论

综上所述，本文提出并研究了一种针对可编程滤光片生成光谱透过率的方法。这种方法基于PCA-LDA机器学习模型，通过对LDA系数的翻转，去除了系数计算中产生的负项，同时基本没有影响性能。相较于以往的方法，无需采集补偿光谱透过率图像，能够实现一次性编码成像。本文在数值模拟的基础上对该方法进行了评价，取得了良好的分类效果，能实现接近于传统方法的性能指标。

基于此种方法编码光谱透过率的可编程滤光片可以促进高光谱数据的采集和后处理的过程的同时实现。这样，与传统的高光谱数据采集相比，速率可提高至少数百倍，基本没有延迟，大大方便了使用，并且完全无需后处理。因此，实际应用中，此种方法可以推动光学成像的物理过程在遥感、生物医学等应用领域更加智能化、信息化、实时化的使用。

此外，所提出的方法同时也提供了一种理论上的可能，即非负的光谱值对整体的影响很小，因此可以在其他方法编码过程同样直接滤除负值，而不会影响光谱透过率的准确度，而其在不同高光谱数据集上的稳定性还有待更多的数据及实验来验证。

致谢

感谢东北大学医学与生物信息工程学院陈硕副教授、张冯頔硕士生以及生物医学光学实验室其他成员的指导和帮助。

基金项目

1) 国家级大学生创新创业训练计划资助项目(200235)编码为201910145235。

2) 中央高校基本科研业务专项资金资助，项目批准号(N182410001)。

NOTES

^*通讯作者。