从四面体到N维单形的棱切球心、热尔岗点、奈格尔点及其坐标公式
Edge-Tangent’s Sphere Center, Gergonne Point, Nagel Point and Their Coordinate Formula from Tetrahedron to N-Simplex
DOI: 10.12677/PM.2021.111019, PDF, HTML, XML,   
作者: 李兴源：广州一智通供应链管理有限公司，广东 广州
关键词: 四面体；棱切球；热尔岗点；奈格尔点；n维单形；Tetrahedron； Edge-Tangent’s Sphere； Gergonne Point； Nagel Point； n-Simplex
摘要: 四面体存在棱切球的充要条件是该四面体的三组对棱之和相等。对于存在棱切球的四面体，本文给出其棱切球心、热尔岗点、奈格尔点的坐标公式，并将这三者的坐标公式推广至存在棱切超球面的n维单形。
Abstract: The sufficient and necessary condition for the tetrahedron to have an edge-tangent’s sphere is that the sum of the three groups of opposite sides is equal in the tetrahedron. For a tetrahedron with an edge-tangent’s sphere, the coordinate formula of the edge-tangent’s sphere center, Gergonne Point and Nagel Point is given in this paper, and the coordinate formulas of these three points are extended to n-simplex with an edge-tangent’s hypersphere.
文章引用：李兴源. 从四面体到N维单形的棱切球心、热尔岗点、奈格尔点及其坐标公式[J]. 理论数学, 2021, 11(1): 131-142. https://doi.org/10.12677/PM.2021.111019

1. 引言

如图1所示，若四面体ABCD存在棱切球，各棱上的切点分别为 M A B 、 M A C 、 M A D 、 M B C 、 M B D 、 M C D 。本文约定O为坐标原点，A、B、C、D四点的坐标分别为 ( x 1 , y 1 , z 1 ) 、 ( x 2 , y 2 , z 2 ) 、 ( x 3 , y 3 , z 3 ) 、 ( x 4 , y 4 , z 4 ) ；设

A M A B = A M A C = A M A D = a , B M A B = B M B C = B M B D = b ,

C M A C = C M B C = C M C D = c , D M A D = D M B D = D M C D = d [1] .

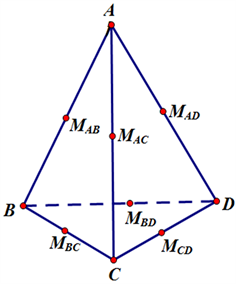
Figure 1. The tangent points on edge-tangent’s sphere of the tetrahedron

图1. 四面体棱切球上的各切点

2. 棱切球心的坐标公式

2.1. 四面体的棱切球心

若四面体ABCD的三组对棱之和相等即存在棱切球，则四面体ABCD的棱切球心坐标为

( F 1 ( a + b ) ( a + c ) ( a + d ) F , F 2 ( a + b ) ( a + c ) ( a + d ) F , F 3 ( a + b ) ( a + c ) ( a + d ) F ) 。其中，

F 1 = | ( O B → − O A → ) ( a ⋅ O B → + b ⋅ O A → ) ( a + b ) ( y 2 − y 1 ) ( a + b ) ( z 2 − z 1 ) ( O C → − O A → ) ( a ⋅ O C → + c ⋅ O A → ) ( a + c ) ( y 3 − y 1 ) ( a + c ) ( z 3 − z 1 ) ( O D → − O A → ) ( a ⋅ O D → + d ⋅ O A → ) ( a + d ) ( y 4 − y 1 ) ( a + d ) ( z 4 − z 1 ) | ,

F 2 = | ( a + b ) ( x 2 − x 1 ) ( O B → − O A → ) ( a ⋅ O B → + b ⋅ O A → ) ( a + b ) ( z 2 − z 1 ) ( a + c ) ( x 3 − x 1 ) ( O C → − O A → ) ( a ⋅ O C → + c ⋅ O A → ) ( a + c ) ( z 3 − z 1 ) ( a + d ) ( x 4 − x 1 ) ( O D → − O A → ) ( a ⋅ O D → + d ⋅ O A → ) ( a + d ) ( z 4 − z 1 ) | ,

F 3 = | ( a + b ) ( x 2 − x 1 ) ( a + b ) ( y 2 − y 1 ) ( O B → − O A → ) ( a ⋅ O B → + b ⋅ O A → ) ( a + c ) ( x 3 − x 1 ) ( a + c ) ( y 3 − y 1 ) ( O C → − O A → ) ( a ⋅ O C → + c ⋅ O A → ) ( a + d ) ( x 4 − x 1 ) ( a + d ) ( y 4 − y 1 ) ( O D → − O A → ) ( a ⋅ O D → + d ⋅ O A → ) | ,

F = | 1 x 1 y 1 z 1 1 x 2 y 2 z 2 1 x 3 y 3 z 3 1 x 4 y 4 z 4 | .

证明：设四面体ABCD的棱切球心为P，由棱切球的性质可知

P M A B ⊥ A B , P M A C ⊥ A C , P M A D ⊥ A D [2] .

再设平面 π 1 、 π 2 、 π 3 分别过 M A B 、 M A C 、 M A D 且分别垂直于AB、AC、AD，则四面体ABCD的棱切球心P即为 π 1 、 π 2 、 π 3 这三个平面的交点。

由定比分点公式可得 M A B 、 M A C 、 M A D 三点的坐标分别为 ( a x 2 + b x 1 a + b , a y 2 + b y 1 a + b , a z 2 + b z 1 a + b ) 、 ( a x 3 + c x 1 a + c , a y 3 + c y 1 a + c , a z 3 + c z 1 a + c ) 、 ( a x 4 + d x 1 a + d , a y 4 + d y 1 a + d , a z 4 + d z 1 a + d ) 。

则平面 π 1 的方程为：

( x 2 − x 1 ) ( x − a x 2 + b x 1 a + b ) + ( y 2 − y 1 ) ( y − a y 2 + b y 1 a + b ) + ( z 2 − z 1 ) ( z − a z 2 + b z 1 a + b ) = 0 .

整理可得：

( a + b ) [ ( x 2 − x 1 ) x + ( y 2 − y 1 ) y + ( z 2 − z 1 ) z ] = ( x 2 − x 1 ) ( a x 2 + b x 1 ) + ( y 2 − y 1 ) ( a y 2 + b y 1 ) + ( z 2 − z 1 ) ( a z 2 + b z 1 ) = ( O B → − O A → ) ( a ⋅ O B → + b ⋅ O A → ) . ①

同理平面 π 2 、 π 3 的方程分别为：

( a + c ) [ ( x 3 − x 1 ) x + ( y 3 − y 1 ) y + ( z 3 − z 1 ) z ] = ( O C → − O A → ) ( a ⋅ O C → + c ⋅ O A → ) . ②

( a + d ) [ ( x 4 − x 1 ) x + ( y 4 − y 1 ) y + ( z 4 − z 1 ) z ] = ( O D → − O A → ) ( a ⋅ O D → + d ⋅ O A → ) . ③

联立① ② ③所组成的线性方程组，并运用克拉姆法则解得 [3]：

x = | ( O B → − O A → ) ( a ⋅ O B → + b ⋅ O A → ) ( a + b ) ( y 2 − y 1 ) ( a + b ) ( z 2 − z 1 ) ( O C → − O A → ) ( a ⋅ O C → + c ⋅ O A → ) ( a + c ) ( y 3 − y 1 ) ( a + c ) ( z 3 − z 1 ) ( O D → − O A → ) ( a ⋅ O D → + d ⋅ O A → ) ( a + d ) ( y 4 − y 1 ) ( a + d ) ( z 4 − z 1 ) | ( a + b ) ( a + c ) ( a + d ) | x 2 − x 1 y 2 − y 1 z 2 − z 1 x 3 − x 1 y 3 − y 1 z 3 − z 1 x 4 − x 1 y 4 − y 1 z 4 − z 1 | = | ( O B → − O A → ) ( a ⋅ O B → + b ⋅ O A → ) ( a + b ) ( y 2 − y 1 ) ( a + b ) ( z 2 − z 1 ) ( O C → − O A → ) ( a ⋅ O C → + c ⋅ O A → ) ( a + c ) ( y 3 − y 1 ) ( a + c ) ( z 3 − z 1 ) ( O D → − O A → ) ( a ⋅ O D → + d ⋅ O A → ) ( a + d ) ( y 4 − y 1 ) ( a + d ) ( z 4 − z 1 ) | ( a + b ) ( a + c ) ( a + d ) | 1 x 1 y 1 z 1 1 x 2 y 2 z 2 1 x 3 y 3 z 3 1 x 4 y 4 z 4 | ,

y = | ( a + b ) ( x 2 − x 1 ) ( O B → − O A → ) ( a ⋅ O B → + b ⋅ O A → ) ( a + b ) ( z 2 − z 1 ) ( a + c ) ( x 3 − x 1 ) ( O C → − O A → ) ( a ⋅ O C → + c ⋅ O A → ) ( a + c ) ( z 3 − z 1 ) ( a + d ) ( x 4 − x 1 ) ( O D → − O A → ) ( a ⋅ O D → + d ⋅ O A → ) ( a + d ) ( z 4 − z 1 ) | ( a + b ) ( a + c ) ( a + d ) | x 2 − x 1 y 2 − y 1 z 2 − z 1 x 3 − x 1 y 3 − y 1 z 3 − z 1 x 4 − x 1 y 4 − y 1 z 4 − z 1 | = | ( a + b ) ( x 2 − x 1 ) ( O B → − O A → ) ( a ⋅ O B → + b ⋅ O A → ) ( a + b ) ( z 2 − z 1 ) ( a + c ) ( x 3 − x 1 ) ( O C → − O A → ) ( a ⋅ O C → + c ⋅ O A → ) ( a + c ) ( z 3 − z 1 ) ( a + d ) ( x 4 − x 1 ) ( O D → − O A → ) ( a ⋅ O D → + d ⋅ O A → ) ( a + d ) ( z 4 − z 1 ) | ( a + b ) ( a + c ) ( a + d ) | 1 x 1 y 1 z 1 1 x 2 y 2 z 2 1 x 3 y 3 z 3 1 x 4 y 4 z 4 | ,

z = | ( a + b ) ( x 2 − x 1 ) ( a + b ) ( y 2 − y 1 ) ( O B → − O A → ) ( a ⋅ O B → + b ⋅ O A → ) ( a + c ) ( x 3 − x 1 ) ( a + c ) ( y 3 − y 1 ) ( O C → − O A → ) ( a ⋅ O C → + c ⋅ O A → ) ( a + d ) ( x 4 − x 1 ) ( a + d ) ( y 4 − y 1 ) ( O D → − O A → ) ( a ⋅ O D → + d ⋅ O A → ) | ( a + b ) ( a + c ) ( a + d ) | x 2 − x 1 y 2 − y 1 z 2 − z 1 x 3 − x 1 y 3 − y 1 z 3 − z 1 x 4 − x 1 y 4 − y 1 z 4 − z 1 |

= | ( a + b ) ( x 2 − x 1 ) ( a + b ) ( y 2 − y 1 ) ( O B → − O A → ) ( a ⋅ O B → + b ⋅ O A → ) ( a + c ) ( x 3 − x 1 ) ( a + c ) ( y 3 − y 1 ) ( O C → − O A → ) ( a ⋅ O C → + c ⋅ O A → ) ( a + d ) ( x 4 − x 1 ) ( a + d ) ( y 4 − y 1 ) ( O D → − O A → ) ( a ⋅ O D → + d ⋅ O A → ) | ( a + b ) ( a + c ) ( a + d ) | 1 x 1 y 1 z 1 1 x 2 y 2 z 2 1 x 3 y 3 z 3 1 x 4 y 4 z 4 | .

2.2. N维单形的棱切球心

由文献 [4] 可知，n维单形 A 0 A 1 ⋯ A n 存在棱切超球的充要条件是其各棱长满足：

A i A j = a i + a j , ( 0 ≤ i ≠ j ≤ n , a i , a j ∈ R + ).

设 A i 的坐标为 ( x i , 1 , x i , 2 , ⋯ , x i , n ) ，参照前面的方法可以求出n维单形 A 0 A 1 ⋯ A n 的棱切超球球心坐标为 ( F 1 F ∏ i = 1 n ( a 0 + a i ) , F 2 F ∏ i = 1 n ( a 0 + a i ) , ⋯ , F n F ∏ i = 1 n ( a 0 + a i ) ) 。其中，

F 1 = | ( O A 1 → − O A 0 → ) ( a 0 ⋅ O A 1 → + a 1 ⋅ O A 0 → ) ( a 0 + a 1 ) ( x 1 , 2 − x 0 , 2 ) ⋯ ( a 0 + a 1 ) ( x 1 , n − x 0 , n ) ( O A 2 → − O A 0 → ) ( a 0 ⋅ O A 2 → + a 2 ⋅ O A 0 → ) ( a 0 + a 2 ) ( x 2 , 2 − x 0 , 2 ) ⋯ ( a 0 + a 2 ) ( x 2 , n − x 0 , n ) ⋮ ⋮ ⋱ ⋮ ( O A n → − O A 0 → ) ( a 0 ⋅ O A n → + a n ⋅ O A 0 → ) ( a 0 + a n ) ( x n , 2 − x 0 , 2 ) ⋯ ( a 0 + a n ) ( x n , n − x 0 , n ) | ,

F 2 = | ( a 0 + a 1 ) ( x 1 , 1 − x 0 , 1 ) ( O A 1 → − O A 0 → ) ( a 0 ⋅ O A 1 → + a 1 ⋅ O A 0 → ) ( a 0 + a 1 ) ( x 1 , 3 − x 0 , 3 ) ⋯ ( a 0 + a 1 ) ( x 1 , n − x 0 , n ) ( a 0 + a 2 ) ( x 2 , 1 − x 0 , 1 ) ( O A 2 → − O A 0 → ) ( a 0 ⋅ O A 2 → + a 2 ⋅ O A 0 → ) ( a 0 + a 2 ) ( x 2 , 3 − x 0 , 3 ) ⋯ ( a 0 + a 2 ) ( x 2 , n − x 0 , n ) ⋮ ⋮ ⋮ ⋱ ⋮ ( a 0 + a n ) ( x n , 1 − x 0 , 1 ) ( O A n → − O A 0 → ) ( a 0 ⋅ O A n → + a n ⋅ O A 0 → ) ( a 0 + a n ) ( x n , 3 − x 0 , 3 ) ⋯ ( a 0 + a n ) ( x n , n − x 0 , n ) | , ⋯ ,

F n = | ( a 0 + a 1 ) ( x 1 , 1 − x 0 , 1 ) ⋯ ( a 0 + a 1 ) ( x 1 , n − 1 − x 0 , n − 1 ) ( O A 1 → − O A 0 → ) ( a 0 ⋅ O A 1 → + a 1 ⋅ O A 0 → ) ( a 0 + a 2 ) ( x 2 , 1 − x 0 , 1 ) ⋯ ( a 0 + a 2 ) ( x 2 , n − 1 − x 0 , n − 1 ) ( O A 2 → − O A 0 → ) ( a 0 ⋅ O A 2 → + a 2 ⋅ O A 0 → ) ⋮ ⋱ ⋮ ⋮ ( a 0 + a n ) ( x n , 1 − x 0 , 1 ) ⋯ ( a 0 + a n ) ( x n , n − 1 − x 0 , n − 1 ) ( O A n → − O A 0 → ) ( a 0 ⋅ O A n → + a n ⋅ O A 0 → ) | ,

F = | 1 x 0 , 1 ⋯ x 0 , n 1 x 1 , 1 ⋯ x 1 , n ⋮ ⋮ ⋱ ⋮ 1 x n , 1 ⋯ x n , n | .

3. 热尔岗(Gergonne)点的坐标公式

对于图1所示的四面体ABCD，设在A、B、C、D四点所对之面上的热尔岗点分别为 G 1 、 G 2 、 G 3 、 G 4 。

3.1. 三角形的热尔岗(Gergonne)点

如图2所示，对于图1所示四面体ABCD中的三角形ABC：A、B、C分别与三角形ABC的内切圆在对边上的切点 M B C 、 M A C 、 M A B 的连线 A M B C 、 B M A C 、 C M A B 三线相交的热尔岗点为 G 4 。由前面引言可知

A B = a + b , B C = b + c , A C = a + c .

则 G 4 的坐标为

O G 4 → = 1 a ⋅ O A → + 1 b ⋅ O B → + 1 c ⋅ O C → 1 a + 1 b + 1 c = b c ⋅ O A → + a c ⋅ O B → + a b ⋅ O C → b c + a c + a b .

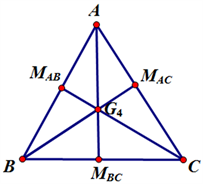
Figure 2. Gergonne points in triangle (Gergonne point)

图2. 三角形的切心(热尔岗点)

证明：由定比分点公式，有

O M B C → = b ⋅ O C → + c ⋅ O B → b + c , O M A C → = a ⋅ O C → + c ⋅ O A → a + c , O M A B → = a ⋅ O B → + b ⋅ O A → a + b .

设

A G 4 G 4 M B C = λ 1 , B G 4 G 4 M A C = λ 2 , C G 4 G 4 M A B = λ 3 ,

则 O G 4 → 有以下三种表示：

O G 4 → = O A → + λ 1 ⋅ O M B C → 1 + λ 1 = ( b + c ) ⋅ O A → + c λ 1 ⋅ O B → + b λ 1 ⋅ O C → ( b + c ) ( 1 + λ 1 ) ,

O G 4 → = O B → + λ 2 ⋅ O M A C → 1 + λ 2 = ( a + c ) ⋅ O B → + a λ 2 ⋅ O C → + c λ 2 ⋅ O A → ( a + c ) ( 1 + λ 2 ) ,

O G 4 → = O C → + λ 3 ⋅ O M A B → 1 + λ 3 = ( a + b ) ⋅ O C → + b λ 3 ⋅ O A → + a λ 3 ⋅ O B → ( a + b ) ( 1 + λ 3 ) .

对上面三式的 O A → 、 O B → 、 O C → 的系数分别进行比较，可得

1 1 + λ 1 = c λ 2 ( a + c ) ( 1 + λ 2 ) = b λ 3 ( a + b ) ( 1 + λ 3 ) , ①

1 1 + λ 2 = a λ 3 ( a + b ) ( 1 + λ 3 ) = c λ 1 ( b + c ) ( 1 + λ 1 ) , ②

1 1 + λ 3 = b λ 1 ( b + c ) ( 1 + λ 1 ) = a λ 2 ( a + c ) ( 1 + λ 2 ) , ③

把上面三式相乘并整理可得

λ 1 λ 2 λ 3 = ( a + c ) ( a + b ) ( b + c ) a b c ;

再分别把① ② ③中的任意两式相乘并整理可得

λ 1 λ 2 = ( a + c ) ( b + c ) c 2 , λ 1 λ 3 = ( a + b ) ( b + c ) b 2 , λ 2 λ 3 = ( a + b ) ( a + c ) a 2 .

解得

λ 1 = a ( b + c ) b c , λ 2 = b ( a + c ) a c , λ 3 = c ( a + b ) a b .

因此

O G 4 → = 1 a ⋅ O A → + 1 b ⋅ O B → + 1 c ⋅ O C → 1 a + 1 b + 1 c = b c ⋅ O A → + a c ⋅ O B → + a b ⋅ O C → b c + a c + a b .

3.2. 四面体的热尔岗(Gergonne)点

对于图1所示的四面体ABCD，由文献 [5] 可知， A G 1 、 B G 2 、 C G 3 、 D G 4 这四条直线在四面体ABCD内交于一点，设该点为G即四面体ABCD的热尔岗(Gergonne)点。

由前面引言可知

A B = a + b , B C = b + c , A C = a + c , A D = a + d , B D = b + d , C D = c + d .

则G的坐标为

O G → = 1 a ⋅ O A → + 1 b ⋅ O B → + 1 c ⋅ O C → + 1 d ⋅ O D → 1 a + 1 b + 1 c + 1 d = b c d ⋅ O A → + a c d ⋅ O B → + a b d ⋅ O C → + a b c ⋅ O D → b c d + a c d + a b d + a b c .

证明：由于

O G 4 → = 1 a ⋅ O A → + 1 b ⋅ O B → + 1 c ⋅ O C → 1 a + 1 b + 1 c ;

同理

O G 1 → = 1 b ⋅ O B → + 1 c ⋅ O C → + 1 d ⋅ O D → 1 b + 1 c + 1 d ,

O G 2 → = 1 a ⋅ O A → + 1 c ⋅ O C → + 1 d ⋅ O D → 1 a + 1 c + 1 d ,

O G 3 → = 1 a ⋅ O A → + 1 b ⋅ O B → + 1 d ⋅ O D → 1 a + 1 b + 1 d .

因为点G为 A G 1 、 B G 2 、 C G 3 、 D G 4 这四条直线的交点，设

A G G G 1 = λ 1 , B G G G 2 = λ 2 , C G G G 3 = λ 3 , D G G G 4 = λ 4 .

则 O G → 有以下四种表示：

O G → = O A → + λ 1 ⋅ O G 1 → 1 + λ 1 = ( 1 b + 1 c + 1 d ) ⋅ O A → + λ 1 ⋅ ( 1 b ⋅ O B → + 1 c ⋅ O C → + 1 d ⋅ O D → ) ( 1 b + 1 c + 1 d ) ( 1 + λ 1 ) ,

O G → = O B → + λ 2 ⋅ O G 2 → 1 + λ 2 = ( 1 a + 1 c + 1 d ) ⋅ O B → + λ 2 ⋅ ( 1 a ⋅ O A → + 1 c ⋅ O C → + 1 d ⋅ O D → ) ( 1 a + 1 c + 1 d ) ( 1 + λ 2 ) ,

O G → = O C → + λ 3 ⋅ O G 3 → 1 + λ 3 = ( 1 a + 1 b + 1 d ) ⋅ O C → + λ 3 ⋅ ( 1 a ⋅ O A → + 1 b ⋅ O B → + 1 d ⋅ O D → ) ( 1 a + 1 b + 1 d ) ( 1 + λ 3 ) ,

O G → = O D → + λ 4 ⋅ O G 4 → 1 + λ 4 = ( 1 a + 1 b + 1 c ) ⋅ O D → + λ 4 ⋅ ( 1 a ⋅ O A → + 1 b ⋅ O B → + 1 c ⋅ O C → ) ( 1 a + 1 b + 1 c ) ( 1 + λ 4 ) .

对上面四式的 O A → 、 O B → 、 O C → 、 O D → 的系数分别进行比较，可得

1 1 + λ 1 = 1 a λ 2 ( 1 a + 1 c + 1 d ) ( 1 + λ 2 ) = 1 a λ 3 ( 1 a + 1 b + 1 d ) ( 1 + λ 3 ) = 1 a λ 4 ( 1 a + 1 b + 1 c ) ( 1 + λ 4 ) ,

1 1 + λ 2 = 1 b λ 3 ( 1 a + 1 b + 1 d ) ( 1 + λ 3 ) = 1 b λ 4 ( 1 a + 1 b + 1 c ) ( 1 + λ 4 ) = 1 b λ 1 ( 1 b + 1 c + 1 d ) ( 1 + λ 1 ) ,

1 1 + λ 3 = 1 c λ 4 ( 1 a + 1 b + 1 c ) ( 1 + λ 4 ) = 1 c λ 1 ( 1 b + 1 c + 1 d ) ( 1 + λ 1 ) = 1 c λ 2 ( 1 a + 1 c + 1 d ) ( 1 + λ 2 ) ,

1 1 + λ 4 = 1 d λ 1 ( 1 b + 1 c + 1 d ) ( 1 + λ 1 ) = 1 d λ 2 ( 1 a + 1 c + 1 d ) ( 1 + λ 2 ) = 1 d λ 3 ( 1 a + 1 b + 1 d ) ( 1 + λ 3 ) .

对上面四式联立可得

a 1 + λ 1 = b 1 + λ 2 = c 1 + λ 3 = d 1 + λ 4 = λ 1 ( 1 b + 1 c + 1 d ) ( 1 + λ 1 ) = λ 2 ( 1 a + 1 c + 1 d ) ( 1 + λ 2 ) = λ 3 ( 1 a + 1 b + 1 d ) ( 1 + λ 3 ) = λ 4 ( 1 a + 1 b + 1 c ) ( 1 + λ 4 ) .

解得

λ 1 = a ( 1 b + 1 c + 1 d ) , λ 2 = b ( 1 a + 1 c + 1 d ) , λ 3 = c ( 1 a + 1 b + 1 d ) , λ 4 = d ( 1 a + 1 b + 1 c ) .

因此

O G → = 1 a ⋅ O A → + 1 b ⋅ O B → + 1 c ⋅ O C → + 1 d ⋅ O D → 1 a + 1 b + 1 c + 1 d = b c d ⋅ O A → + a c d ⋅ O B → + a b d ⋅ O C → + a b c ⋅ O D → b c d + a c d + a b d + a b c .

3.3. N维单形的热尔岗(Gergonne)点

若n维单形 A 0 A 1 ⋯ A n 存在棱切超球，且各棱长满足：

A i A j = a i + a j , ( 0 ≤ i ≠ j ≤ n , a i , a j ∈ R + ).

设 A 0 、 A 1 、 ⋯ 、 A n 各点在其所对之面上的热尔岗点分别为 G 0 、 G 1 、 ⋯ 、 G n 。则诸直线 A 0 G 0 、 A 1 G 1 、 ⋯ 、 A n G n 在n维单形 A 0 A 1 ⋯ A n 内交于一点，设该点为G即n维单形 A 0 A 1 ⋯ A n 的热尔岗点，其坐标为

O G → = ∑ i = 0 n 1 a i ⋅ O A i → ∑ i = 0 n 1 a i .

证明：前面已经证明了当 n = 3 时命题成立。假设当 n = k 时命题同样成立 ( k ≥ 3 , k ∈ Z ) ，现使用数学归纳法证明当 n = k + 1 时命题依然成立。由归纳假设可得

O G i → = ∑ j = 0 k + 1 1 a j ⋅ O A j → − 1 a i ⋅ O A i → ∑ j = 0 k + 1 1 a j − 1 a i , 0 ≤ i ≤ k + 1 .

若点G为 A 0 G 0 、 A 1 G 1 、 ⋯ 、 A k + 1 G k + 1 这 k + 2 条直线的交点，设

A i G G G i = λ i .

则

O G → = O A i → + λ i ⋅ O G i → 1 + λ i = ( ∑ j = 0 k + 1 1 a j − 1 a i ) ⋅ O A i → + λ i ⋅ ( ∑ j = 0 k + 1 1 a j ⋅ O A j → − 1 a i ⋅ O A i → ) ( ∑ j = 0 k + 1 1 a j − 1 a i ) ( 1 + λ i ) .

对上式中的i分别取0到 k + 1 之间的各个整数值，并对 O A i → 的系数分别进行比较，可得

1 1 + λ i = λ j ⋅ 1 a i ( ∑ i = 0 k + 1 1 a i − 1 a j ) ( 1 + λ j ) , ( 0 ≤ i ≠ j ≤ k + 1 ) .

对上式中的i、j取遍各种符合条件的取值并联立可得

a i 1 + λ i = λ i ( ∑ j = 0 k + 1 1 a j − 1 a i ) ( 1 + λ i ) .

解得

λ i = a i ( ∑ j = 0 k + 1 1 a j − 1 a i ) .

因此

O G → = ∑ i = 0 k + 1 1 a i ⋅ O A i → ∑ i = 0 k + 1 1 a i .

故 n ≥ 3 时命题均成立。

4. 奈格尔(Nagel)点的坐标公式

由文献 [6] 可知，若四面体ABCD存在内棱切球，则四面体ABCD在各棱的临棱区均存在侧棱切球。如图3所示，对于同时存在内棱切球和6个侧棱切球的四面体ABCD，其6个侧棱切球在各棱上的切点分别为 M ′ A B 、 M ′ A C 、 M ′ A D 、 M ′ B C 、 M ′ B D 、 M ′ C D 。

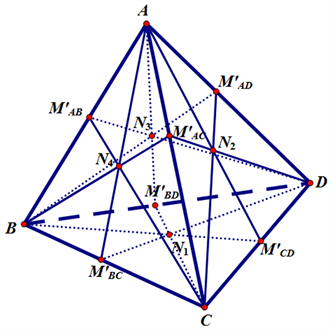
Figure 3. The tangent points of six chamfered edge- tangent’s sphere on each edge of the tetrahedron

图3. 四面体6个侧棱切球在各棱上的切点

4.1. 三角形的奈格尔(Nagel)点

对于图3所示的四面体ABCD，根据侧棱切球的性质可知：直线 B M ′ C D 、 C M ′ B D 、 D M ′ B C 的交点 N 1 为三角形BCD的奈格尔点；直线 A M ′ C D 、 C M ′ A D 、 D M ′ A C 的交点 N 2 为三角形ACD的奈格尔点；直线 A M ′ B D 、 B M ′ A D 、 D M ′ A B 的交点 N 3 为三角形ABD的奈格尔点；直线 A M ′ B C 、 B M ′ A C 、 C M ′ A B 的交点 N 4 为三角形ABC的奈格尔点。根据三角形等距共轭点的性质，设

B M ′ A B = C M ′ A C = D M ′ A D = a , A M ′ A B = C M ′ B C = D M ′ B D = b ,

A M ′ A C = B M ′ B C = D M ′ C D = c , A M ′ A D = B M ′ B D = C M ′ C D = d .

则 N 1 、 N 2 、 N 3 、 N 4 的坐标分别为

O N 1 → = b ⋅ O B → + c ⋅ O C → + d ⋅ O D → b + c + d ,

O N 2 → = a ⋅ O A → + c ⋅ O C → + d ⋅ O D → a + c + d ,

O N 3 → = a ⋅ O A → + b ⋅ O B → + d ⋅ O D → a + b + d ,

O N 4 → = a ⋅ O A → + b ⋅ O B → + c ⋅ O C → a + b + c [7] .

4.2. 四面体的奈格尔(Nagel)点

对于图3所示的四面体ABCD， A N 1 、 B N 2 、 C N 3 、 D N 4 这四条直线在四面体ABCD内交于一点，设该点为N即四面体ABCD的奈格尔(Nagel)点。又

A B = a + b , B C = b + c , A C = a + c , A D = a + d , B D = b + d , C D = c + d .

则N的坐标为

O N → = a ⋅ O A → + b ⋅ O B → + c ⋅ O C → + d ⋅ O D → a + b + c + d .

证明从略，可参考前面四面体热尔岗点坐标的计算方法。

4.3. N维单形的奈格尔(Nagel)点

若n维单形 A 0 A 1 ⋯ A n 存在棱切超球，且各棱长满足：

A i A j = a i + a j , ( 0 ≤ i ≠ j ≤ n , a i , a j ∈ R + ).

设 A 0 、 A 1 、 ⋯ 、 A n 各点在其所对之面上的奈格尔点分别为 N 0 、 N 1 、 ⋯ 、 N n 。则诸直线 A 0 N 0 、 A 1 N 1 、 ⋯ 、 A n N n 在n维单形 A 0 A 1 ⋯ A n 内交于一点，设该点为N即n维单形 A 0 A 1 ⋯ A n 的热尔岗点，其坐标为

O N → = ∑ i = 0 n a i ⋅ O A i → ∑ i = 0 n a i .

证明从略，同理可参考前面对n使用数学归纳法进行证明。

参考文献

[1] 贺斌. 四面体存在棱切球的一个充要条件[J]. 中学数学月刊, 1998(3): 46.
[2] 翁玉中. 关于多面体的棱切球的存在性[J]. 中学数学月刊, 1997(8): 14-16.
[3] 赵艳. 克拉姆法则证明的新方法与几何解释[J]. 数学教学研究, 2012, 31(3): 53-54.
[4] 林祖成. n维单形的棱切超球[J]. 数学实践与认识, 1995(4): 90-93.
[5] 曾建国. 四面体的约尔刚(Gergonne)点[J]. 数学通讯, 2009, 12(2): 31-32.
[6] 曾建国. 四面体的侧棱切球与奈格尔(Nagel)点[J]. 中学数学教学, 2010(4): 58-60.
[7] 邓胜. 三角形特殊点的一般坐标公式[J]. 数学通讯, 1998(8): 24-26.

为你推荐