基于BP神经网络的横流开式空气源换热塔性能预测

Performance Prediction of Cross Flow Open Air Source Temperature Heat Transfer Tower Based on BP Neural Network

摘要: 本文基于BP神经网络预测吸热工况下空气源换热塔的热性能，通过改变空气源换热塔的循环溶液流量、风量和进口溶液温度，记录不同工况下的测量参数，利用BP神经网络处理试验数据。网络采用三层结构，隐含层神经元个数为5个，以溶液流量、溶液进口温度、风量、干球温度和盐球温度为输入参数，空气源换热塔吸热效率为输出值。吸热效率预测值和实测值的相关系数、平均相对误差、均方根误差分别为0.995、1.3775%、6.178 × 10⁻³。结果表明，BP神经网络可以准确预测空气源换热塔吸热工况下的性能，对空气源换热塔热泵系统的运行和设计有重要意义。

Abstract: This paper predicts the thermal performance of air source heat exchange tower under endothermic condition on BP neural network, by changing the circulating solution flow rate, air volume and inlet solution temperature of the air source heat exchanger tower, the measured parameters under dif-ferent working conditions were recorded, and the test data were processed by BP neural network. The network adopted a three-layer structure, and the number of hidden layer neurons was 5. The solution flow rate, solution inlet temperature, air volume, dry bulb temperature and salt bulb tem-perature were taken as input parameters, and the heat absorption efficiency of the air source heat exchanger was taken as output value. The correlation coefficient, mean relative error and root mean square error of predicted and measured endothermic efficiency are respectively 0.995, 1.3775% and 6.178 × 10⁻³. The results show that BP neural network can accurately predict the performance of the air source heat exchanger under the condition of absorption, which is of great significance to the operation and design of the heat pump system of the air source heat exchanger.

1. 引言

空气源换热塔热泵系统以低温防冻溶液为循环介质，从环境中获取可再生的空气热能 [1]，实现低能耗供暖，被广泛用于夏热冬冷区域的建筑中 [2]。

空气源换热塔作为热泵系统中与空气换热的核心设备，是在冷却塔的基础上发展而来的，其换热效率直接影响系统的运行和效能。通常研究空气源换热塔的换热性能以热质传递为基础的物理模型和以实测数据为基础的试验分析入手。空气源换热塔内湿空气与溶液之间有着复杂热质传递关系，在理论分析时需借助大量假设条件，影响了研究结果的准确性，而完全依赖试验研究则需在原型塔的测试上耗费大量资源和时间。

BP (Back Propagation)神经网络是一种模拟大脑神经系统结构和功能的复杂网络，无需描述变量之间可能存在的联系，只要通过分析一批实测数据，就可以建立输入与输出之间的非线性关系，对系统的期望值进行预测。近年来，BP神经网络以其非线性映射、自学习、自适应、容错能力等优势在采暖、空调、热泵等领域得到广泛的应用 [3] [4] [5] [6]。

目前，有一些学者通过神经网络对空气源换热塔的换热性能进行研究，其中大部分研究是针对冷却塔。宋嘉梁等 [7] 使用神经网络对自然通风冷却塔热力性能进行预测；Xu等 [8] 以四层神经网络为核心，对机械通风冷却塔出口水温进行预测；M. Hosoz [9] 利用人工神经网络模型对逆流冷却塔的冷却性能进行预测；Gao等 [10] 建立三层BP神经网络对侧风条件下的冷却塔性能进行预测。Wu等 [11] 基于BP神经网络模型对热泵系统在制热模式下冷却塔逆用吸热的性能进行研究。但由于空气源换热塔的吸热以显热为主，需更大体积，同时要有防雨水进入等措施，结构上与冷却塔有一定差别，气水比和淋水密度与冷却塔也不尽相同。所以本文直接用以冬季吸热为目的的空气源换热塔原型机进行实验，利用获取的实验数据，采用三层BP神经网络模型对空气源换热塔换热性能进行预测，结果会更加准确，对空气源换热塔热泵系统的运行和调试更具有参考价值。

2. 实验测试

2.1. 实验装置

实验系统如图1所示：被测试对象为两面进风的横流型空气源换热塔，其两侧各有PVC薄膜填料150片，单侧进风面尺寸为2.8 m × 3 m，设计流量为300 m³/h。

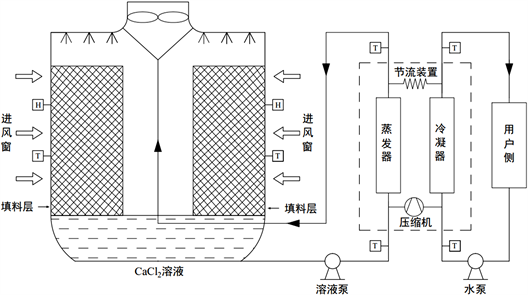
Figure 1. Air source heat transfer tower system diagram

图1. 空气源换热塔系统图

热泵机组额定供热量350 kw，热泵系统使用制冷剂为一氯二氟甲烷(R22)，溶液循环采用密度为1200 kg/m³的氯化钙(CaCl₂)溶液，其因具有凝固点较低、吸热性能较强、稳定性较好被选为二次制冷剂，使空气源换热塔热泵系统可以更好的从低温空气中提取热量。在吸热工况下，喷淋系统经溶液泵将CaCl₂溶液均匀喷洒在填料上，与进入空气源换热塔内的空气进行热质交换，吸取空气中的低品位热能，进入蒸发器后将热量传递给制冷剂，冷凝器侧循环水同时被加热，送到用户侧，完成供热循环。

2.2. 测试系统

空气源换热塔性能测试所需要的参数包括大气压、环境干球温度与相对湿度、CaCl₂溶液的进出口温度、溶液流量和进塔风速，同时监控溶液密度，通过加CaCl₂使其稳定不变。所有温度均自动采集，采集频率为每秒1次，以每分钟的平均值为瞬时输出值，计算时取连续30 min内波动均不超过±0.2℃的数据段数据的平均值作为测量值。表1为测量所需仪器的详细信息。

Table 1. Measuring instrument parameters

表1. 测量仪器参数

为了保证进塔风速测量的准确性，两侧进风窗按等面积法划分为4 × 4的矩形区域，使用风速仪在每个矩形区域的中心进行测试，最后取平均值。

实验采用控制变量法，在不同干球温度和盐球温度下构成特定的实验工况，分别测得溶液出口温度，计算吸热效率。实验中测得的样本数据范围见表2：

Table 2. Sample data range

表2. 样本数据范围

2.3. 性能指标

将吸热效率η作为评价空气源换热塔的性能指标，表示空气源换热塔实际换热能力与极限换热能力的接近程度。吸热效率由式(1)计算得出：

$\eta =\frac{T_{so}-T_{si}}{T_{so}-T_{aw}}$ (1)

式中：T_si——为溶液入口温度；T_so——为溶液出口温度；T_aw——为盐球温度。

3. BP神经网络建模

3.1. 网络原理及参数选取

BP神经网络是一种按误差反向传播算法训练的多层前馈神经网络，由信息的前向传递和误差的反向传播两个过程构成。在前向传递中，从输入层和隐含层到输出层逐层处理输入信号，每一层神经元状态只对下一层神经元状态有影响。如果输入层与期望输出不匹配，则执行反向传播。误差的反向传播是一个权值调整的过程，根据预测误差调整网络系数，从而使BP神经网络预测结果逐渐接近期望结果。网络流程如图2所示：

Figure 2. BP network flow chart

图2. BP网络流程图

实验采取单个隐含层的三层BP神经网络来处理复杂、非线性目标。如图3所示，输入层中选取五个主要影响因素作为输入参数，分别为溶液进口温度T_si、进口空气干球温度T_a、盐球温度T_aw、溶液流量Q_s和风量G_a，而将空气源换热塔吸热效率η作为输出值。

Figure 3. BP network diagram

图3. BP网络示意图

3.2. 网络训练

网络采用线性函数purelin作为传递函数，网络训练采用trainlm函数对网络进行测试。共采集250组数据作为输入–输出对，其中随机取175组应用于训练集，其余75组用于网络测试。为了使网络的收敛性有较快训练速度，数据在输入之前进行了归一化处理，同样，数据在输出后也进行了反归一化。本文选取的归一化函数是mapminmax函数，归一化定义见式(2)，反归一化定义见式(3)：

$y=\frac{x-x_{\min }}{x_{\max }-x_{\min }}$ (2)

$x=x_{\min }+y\left(x_{\max }-x_{\min }\right)$ (3)

式中：x——为被归一化的值；y——为归一化后的值。

3.3. 网络性能指标

本文对空气源换热塔吸热效率的预测准确性取决于BP神经网络的拟合性能，其基于网络之间的回归分析进行评估。采用相关系数r，平均相对误差MRE和均方根误差RMSE作为评测空气源换热塔网络拟合性能的特征参数。

相关系数r按式(4)计算，其绝对值越接近1，相关性越高。

$r=\frac{\mathrm{cov}\left(A_i,P_i\right)}{\sqrt{\mathrm{cov}\left(A_i,A_i\right)\cdot \mathrm{cov}\left(P_i,P_i\right)}}$ (4)

式中：A_i——为实际输出值；P_i——为网络预测值。

平均相对误差MRE是绝对误差与实测值之比的平均值，按式(5)计算：

$MRE=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}\left|100\frac{\left(A_i-P_i\right)}{A_i}\right|}$ (5)

式中：N——为样本个数。

均方根误差RMSE又称回归标准差，反映测量的精确度，按式(6)计算：

$RMSE=\sqrt{\frac{1}{N}-{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\left(A_i-P_i\right)}^2}}$ (6)

3.4. 确定隐含层节点数

神经网络拟合性能的主要影响因素是隐含层神经元个数。但到目前为止，还没有一种准确的方法来确定最优隐含层的神经元个数，通常隐含层神经元个数由式(7)得出估计值 [12]：

$k<{\displaystyle \underset{i=0}{\overset{n}{\sum }}{C}_M^i}$ (7)

式中：k——为样本数；M——为隐含层神经元个数；n——为输入层神经元个数。

当 $i>M$ 时，取 $C_M^i=0$

M的取值还可参考式(8)~(11)：

$M=\sqrt{n+m}+c$ (8)

式中：m为输出层单元数，c为常数，取值为[0, 10]。

$M={\log }_{2}n$ (9)

当只有一个隐层时，隐含层神经元个数为 [13]：

$M=\sqrt{mn}$ (10)

另一种确定隐含层神经元个数的方法，采取最小二乘法进行拟合的公式 [14]：

$M={\left(0.43mn+0.12m^2+2.54n+0.77n+0.35\right)}^{1/2}+0.51$ (11)

综合以上公式，隐含层神经元个数范围选取为[2, 6]。

利用选取的三层BP神经网络模型对[2, 6]隐含层神经元个数分别对175组数据进行训练，并保证迭代次数能够使平均相对误差MRE随迭代次数增加而趋于稳定，训练结束后，将其它75组数据的模型预测值与实测值进行对比，得出的拟合性能特征参数见表3。

Table 3. The test results of the number of neurons in different hidden layers

表3. 不同隐含层神经元个数时的测试结果

从表3可知，当隐含层神经元个数为5个时，空气源换热塔吸热效率实测值与预测值的相关系数r较高且平均相对误差MRE与均方根误差RMSE较小。因此隐含层神经元个数为5个，最终确定的BP网络为5-5-1结构。

4. 结果与分析

利用5-5-1结构的三层BP神经网络模型对空气源换热塔吸热效率进行预测，学习速率为0.1，隐含层数为5，训练函数为trained时，平均相对误差MRE随迭代次数增加的变化趋势见图4，训练过程中，随着迭代次数的不断增加，平均相对误差MRE总体下降，最后趋于稳定。采用相关系数r或者均方根误差RMSE，同样可以判断稳定性，本文不再赘述。

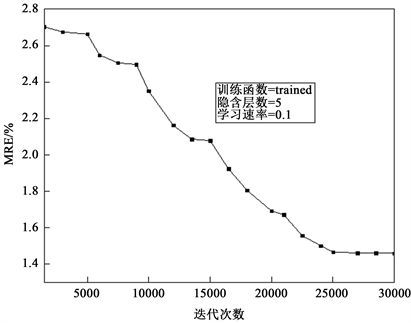
Figure 4. The average relative error varies with the number of iterations

图4. 平均相对误差随迭代次数的变化

所用75组数据在选取30,000次迭代时的预测值与实测值偏差如图5所示：

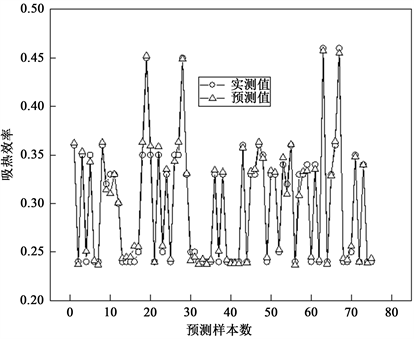
Figure 5. Comparison of predicted and measured η

图5. η的预测值与实测值对比

由图5可知，空气源换热塔吸热效率大部分预测值与实测值是比较吻合的。其中最大误差值是2.169 × 10⁻²，最小误差值是1.25 × 10⁻⁴。吸热效率预测值与实测值的评价指标有相关系数、平均相对误差、均方根误差在表3中已给出，分别为0.995，1.3775%，6.178 × 10⁻³。

将空气源换热塔吸热效率实测值和预测值分别作为横纵坐标轴，可比较两者偏差的程度，见图6。为了显示BP神经网络的准确性，图6中有一条表示预测良好的直线和表示偏差程度在±5%内的两条误差线。

Figure 6. The degree of deviation between measured and predicted values

图6. 实测值与预测值的偏差程度

由图6可知，大部分样本点都位于±5%的偏差范围内，由于换热塔性能受到环境温湿度的影响，空气湿球温度的波动导致个别样本点偏差较大，偏差出于5%至10%之间。在拟合直线时发现，根据样本点拟合的直线比y = x略微向上偏移，因此预测值在总体上略微大于实测值。

5. 结论

本文建立了用于开式横流空气源换热塔吸热效率性能测试的BP神经网络模型。采用三层BP神经网络，输出的参数为空气源换热塔吸热效率η。结果表明，空气源换热塔的热力性能可以在可靠性的数据范围内使用神经网络进行建模。通过有限的实测数据，不需要理解空气源换热塔的热质传递过程和处理复杂的数学模型，可以对空气源换热塔性能进行准确的预测，节省大量时间和资金。

本文采用相关系数、平均相对误差、均方根误差作为空气源换热塔网络模型评价指标，结果分别为0.995，1.3775%，6.178 × 10⁻³。从预测结果来看，本实验建立的空气源换热塔BP神经网络模型较好，可以准确预测空气源换热塔热性能，为换热塔在冬季吸热工况下性能的预测提供了思路和方法。

基金项目

国家自然科学基金(编号：51976127)。

NOTES

^*通讯作者。