聚光光热腔式集热器的结构优化

Structure Optimization of Concentrating Solar-Thermal Cavity Receiver

摘要: 聚光光热集热器在光热发电系统中是一个关键部件，其性能直接影响光热电站的效率，因此对其结构优化研究有着重要的意义。本文对5种不同形状的集热器进行了数值模拟，结果表明球形集热效果最佳；针对球形集热器分析了不同开口比(S1/S2)对光学性能的影响以及不同倾角对对流热损的影响。结果表明：随着S1/S2的降低，集热器的反射光损减小，结合集热器的内部温度场得出最佳开口比为1/8；随着采光口面积增大，集热器内部低温对流换热区域增大，对流热损增大；随着采光口倾角增加，对流热损随之下降。

Abstract: The concentrating solar-thermal collector is a key component in the solar-thermal power generation system, the performance of which directly affects the efficiency of solar-thermal power plant. Therefore, it is of great significance for the structural optimization research of the concentrator. In this paper, five kinds of collectors with different shapes are numerically simulated. The results show that the spherical collector is the most efficient one. The effects of different aperture ratios (S1/S2) on optical performance and different inclination angles on convective heat loss are analyzed for the spherical collectors. The results show that the reflected light loss of the collector decreases with the reduction of S1/S2, and the optimal aperture ratio of the collector is 1/8 combined with the internal temperature field. With the increase of the lighting port area, the area of low-temperature convective heat transfer inside the collector increases, and the convective heat loss increases at the same time. Convective heat loss decreases with the increase of inclination angles.

1. 引言

太阳能聚光光热系统主要由聚光器、集热器和卡诺循环发电装置或斯特林机循环构成。其中，集热器件是接收太阳能并运用循环工质进行光–热转换的重要装置，光热转换效率直接影响着出口端工质的温度高低，也间接影响着后续做功工质的热电转换效率，因此可以认为集热器件的热性能是整个光热系统效率的重要影响因素。

目前，国内外越来越多学者对聚光光热集热器进行了研究，1991年，Pitz-Paal等 [1] 创新地在吸热体外表面处添加了玻璃窗，使得空气的流道具有选择性，实验数据表明，空气出口温度超过600℃，减弱了辐射热损。1993年，Steinfeld和Schubnel [2] 针对太阳能集热器采光口对热性能的影响程度进行了研究，定义采光口的最优尺寸范围。2008年，Sendhil Kumar N.等 [3] 对比了两种形状的太阳能集热器，结果表明：集热器的几何形状与倾斜角度对热损的占比影响较大。2009年，杨敏林等人 [4] 针对非均匀热流的现实情况采取缠绕电阻丝利用电加热的模拟方式进行试验研究，实验结果表明不均匀的热流密度会引发集热器管壁温度场分布不均的问题。2012年，毛青松 [5] 等人采用商业光学软件，以蒙特卡洛光迹追踪法为理论基础，分析了不同开口尺寸的腔式集热器的光学特性和热学特性，发现采光口尺寸的变化仅能改变对流热损的数值大小，而对辐射热损的影响微乎其微。2014年，Flesch等人 [6] 针对集热器的摆放位置和环境风速等因素对集热器对流热损的影响进行了研究，结果表明，无风时对流热损随安装角度的增加而减少。2015年，Srihari和Reddy [7] 研究了各种参数的影响，例如直径开口比，倾斜角度，工作温度，绝缘层厚度对热损失的影响。2016年，王俊杰 [8] 针对集热器的安装倾角进行了对比分析，当采光口面朝地面时，其热损随集热器开口处的弯度参数变化而改变。2017年，何雅玲 [9] 团队针对目前仅采用单管为实验对象的研究现状提出了导热–对流–辐射耦合的换热模拟方式，并在此基础上对热应力进行了研究，分析了影响薄壁管材热应力的最大应力为切向应力。2018年，Pavlovic等人 [10] 对螺旋形和圆锥形集热器的光学性能与传热性能进行了研究，得出圆锥形集热器的综合性能要比螺旋形集热器更优。2019年，SI-QUAN Z.等人 [11] 研究了不同形状集热器，得出球形集热器的光学效率最佳，分析了不同开口比对光学性能的影响以及不同倾角对对流热损的影响。2020年，Reyhaneh Loni等人 [12] 通过实验研究了具有不同形状腔接收器和纳米流体的太阳能碟式集热器的热性能，结果表明半球形的太阳能碟式集热器的热特性效果最佳。

综上所述，聚光光热集热器的结构设计对光热转换效率有很大影响，本文以腔式集热器作为研究对象，分析集热器件的传热特性，并对集热器件的结构参数进行设计优化。

2. 腔式集热器的能源平衡

腔式集热器存在四部分热损：反射热损失、导热热损失、对流热损失、辐射热损失。一般太阳能集热器外壁面存在保温层因此可以忽略导热热损失，只考虑反射热损失、对流热损失、辐射热损失。

2.1. 反射热损

在太阳能光热系统中，常利用高倍反射聚光器件将太阳光线转变为高热流密度光能并经由采光口入射至集热器内部，高倍光线在其内部多次发生反射，其中有一部分光线透过采光口逸散，造成一定数量光线的损失，间接造成能量损失，此称为反射光损( $Q_{ref}$ )。其中当忽略壁面材料反射率受温度变化的影响时，可近似计算反射光损的公式为 [13]：

$Q_{ref}=\rho \cdot Q_{in}\cdot F_r$ (1)

$F_r=A_{ape}/A_{re}$ (2)

式中： $\rho$ ——集热器件壁面材料的反射率，本文取值0.1；

$Q_{in}$ ——总入射光能(W)；

$A_{ape}$ ——集热器件采光口面积(m²)；

$A_{re}$ ——集热器件表面面积(m²)。

2.2. 对流热损

集热器件内壁与环境存在温差而产生对流作用，其对流热损( $Q_{conv}$ )分为自然对流热损( $Q_{conv,nc}$ )和强制对流热损( $Q_{conv,fc}$ )。当环境风速为零，称为自然对流热损，主要受集热器件和环境之间存在不均匀温度场这一变量影响，本文计算的自然对流热损公式如式(3) [14]：

$Q_{conv,nc}={\alpha }_{nc}\cdot A_{re}\cdot \left(T_w-T_a\right)=0.59{\left(GrPr\right)}^{1/4}\left(\frac{\lambda }{L}\right)A_{re}\left(T_w-T_a\right)$ (3)

式中： ${\alpha }_{nc}$ ——自然对流换热系数(W/(m²∙K))；

L——集热器件采光口当量直径(m)；

$\lambda$ ——空气的导热系数(W/(m∙K))；

Gr——格拉晓夫数；

Pr——空气的普朗特数；

$T_w$ ——吸热管正面壁温(K)；

$T_a$ ——环境温度(K)。

$Gr=\frac{g{a}_v\Delta t{L}^3}{v^2}$ (4)

式中：g——重力加速度(m/s²)；

$a_v$ ——体积变化系数(对于理想气体即等于绝对温度的倒数)；

∆t——温差(K)；

L——特征尺度(m)；

v——运动粘度(m²/s)；

注：当Gr处于1.43 × 10⁴~3 × 10⁹时，本公式才适用；本文中各结构参数下的Gr数值大约为6.45 × 10⁵~2.83 × 10⁷。

当环境风速不为零，称为强制对流热损，其对流热损不仅仅受不均匀温度场的影响，还受环境风速的影响，本文采用的强制对流热损公式如下 [12]：

$Q_{conv,fc}={\alpha }_{fc}\cdot A_{re}\cdot \left(T_w-T_a\right)=0.193R{e}^{0.618}P{r}^{1/3}\left(\frac{\lambda }{L}\right)A_{re}\left(T_w-T_a\right)$ (5)

式中： ${\alpha }_{fc}$ ——强制对流换热系(W/(m²∙K))。

2.3. 辐射热损

集热器件对于大空间环境而言，体积无穷小，集热器内侧吸热管表面简化为灰体表面，即其辐射热损( $Q_{rad}$ )可由以下公式简化计算 [15]

$Q_{rad}={\epsilon }_{eff}\cdot \sigma \cdot \left(T_w^4-T_a^4\right)\cdot A_{re}$ (6)

${\epsilon }_{eff}=\frac{{\epsilon }_w}{{\epsilon }_w+\left(1-{\epsilon }_w\right)\cdot F_r}$ (7)

$F_r=A_{ape}/A_{re}$ (8)

式中： $\sigma$ ——史蒂芬·玻尔兹曼常数；

${\epsilon }_w$ ——吸热管的发射率，本文取值为0.3；

$A_{ape}$ ——集热器件采光口面积(m²)；

${\epsilon }_{eff}$ ——腔体的有效发射率。

3. 腔式集热器的数值模拟方法

3.1. 腔式集热器的几何模型

本文研究的太阳能腔式集热器(以球形为例)的基本物理模型如图1所示。图中S₁表示集热器采光口的面积大小，S₂表示集热器内壁的面积大小，此外，铜具有良好的导热性，因此，可将集热器的壁面简化为一整体 [16]。集热器外壁包裹着约10 mm厚的不透明保温材料，可将其认为绝热壁面，忽略了保温层内部的热传导。

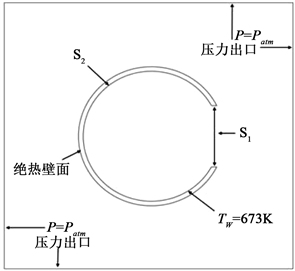
Figure 1. Model and boundary conditions of sphericalcavity receiver

图1. 球形腔式集热器模型与边界条件

在实际情况中，集热器在大环境中进行辐射、对流散热，因此，该种模拟属于大空间散热情况，为使计算域的大小不影响集热器的热流动，需将环境空间的计算域增大至集热器面积30倍以上，规避计算域过小所带来的计算偏差。因此，选择将计算域设为2.0 m × 2.0 m的正方形区域。在数值模拟研究中，本文采用ICEM软件对几何进行网格划分如图2，利用Fluent软件对集热器的热学性能进行模拟。

Figure 2. Meshing

图2. 网格划分

3.2. 求解算法及边界条件

本文采用压力基求解器进行模拟计算，算法选用SIMPLE算法求解速度压力方程。太阳能在经过高倍聚焦后再由采光口进入腔式集热器内部时，其光线分布较为复杂，因此，为简化计算，将边界条件简化为等壁面温度或均匀热流密度。为方便对集热器的热效率进行数值分析，做出以下假设：

1) 模拟边界条件采用 $P=P_{atm}$ 压力入口边界条件；

2) 瑞利数 $Ra=GrPr=\frac{g\beta \text{Δ}T{D}^3}{{\upsilon }^2}Pr$ 判定集热器内部流体的流动状态，本文瑞利数小于10⁸，因此，假设为稳态层流流动；

3) 空气密度的变化是由温度变化引起的，采取Boussinesq近似和不可压缩理想气体模型；

4) 集热器内壁面温度恒定为673 K [17]；

5) 外壁面为绝热边界层，不考虑保温层侧的导热现象。

4. 集热器结构参数优化

4.1. 集热器形状的最优选择

先保持采光口面积和集热器内壁面面积相同，利用Fluent模拟软件对5种不同形状结构的集热器进行静态热性能分析，温度云图如图3所示，其统一条件为：内壁面温度为673 K，采光口半径均为60 mm，安装倾角(采光口所处平面的法向与水平面的夹角)为0℃。

由图3可知：各类集热器内部的空气被加热升温，按高温滞留区的平均温度大小可分为：球形>六棱柱形 > 椭球形 > 圆台形 > 圆柱形，其中球形集热器内部高温区域的平均温度最大，所处温度数值范围为409 K~673 K，其值远远高于其余三种集热器，说明球形这一结构的集热器保温效果最优。

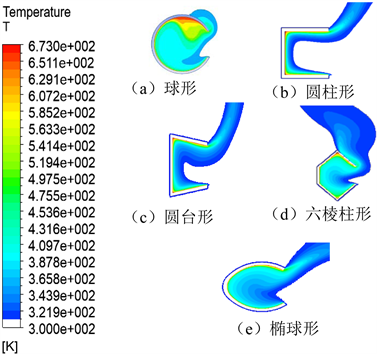
Figure 3. Temperature contour of different shape collectors

图3. 不同形状集热器的温度云图

4.2. 采光口面积与集热器内壁面比(S₁/S₂)的设计优化

控制腔式集热器采光口半径大小R₁ = 60 mm和倾角(0˚)为固定量，通过改变腔体内壁面的面积来控制S₁/S₂的比值变化(1/4, 1/6, 1/8, 1/10)，以研究不同比值下集热器的对流和辐射热性能。

4.2.1. 集热器光学性能模拟

改变采光口面积与集热器内壁面比值(S₁/S₂)获得不同尺寸比例下的反射光损以及球形集热器内部的光线分布状况。光学性能的监测系统如图4所示，假设抛物面聚光器上方存在有一虚拟平面光源，其投射出来的光线相互平行且垂直于聚光器开口平面，光线足够多且呈现均匀分布，其光源形状为圆盘形，直径为4 m，辐射能密度为1000 W/m²。聚光器表面为理想抛物面，聚光器的直径与光源一致，焦距为2 m，并且腔式集热器的开口平面恰好位于抛物面聚光器的焦点处。利用基于蒙特卡洛光线追踪法的商业软件进行集热器的光学性能研究，计算结果如表1所示。

其中，反射光损率的计算公式如下：

${\rho }_{ref}=n_{out}\times \frac{1-\alpha }{N}$ (9)

式中： ${\rho }_{ref}$ ——反射光损率/%；

$n_{out}$ ——采光口逸出的一次反射光线数量；

$\alpha$ ——腔体内壁材料对光线的吸收率，本文取0.9；

N——自聚光器面进入腔体内部的光线总量。

观察表1可发现，当S₁/S₂比值减小时，集热器的光线逃逸量愈发减少。从集热器的结构尺寸大小来看，当S₁/S₂比值减小时，光线在腔体内部多次反射的概率增加，降低了光线逃逸的可能。从反射光损率的大小来看，比值为1/4~1/8时，反射光损率的下降速率明显大于1/10时，因此可以得出结论，当S₁/S₂比值减小至一定时，再对其进行减小尺寸比例已无法使得反射光损率得到更为明显的降低，结合集热器的设计及安装要求可以得出当S₁/S₂比值为1/8时，集热器光学效率较优，这与SI-QUAN Z [10] 的模拟结果趋势一致。

Figure 4. Collector optical performance monitoring system

图4. 不同S₁/S₂比值下球形集热器的光线统计

Table 1. Light statistics of spherical collectors under different S1/S2 ratios

表1. 不同S₁/S₂比值下球形集热器的光线统计

4.2.2. 集热器热性能分析

如图5所示腔式集热器在采用不同S₁/S₂比值时所对应的温度云图。通过图5可以看出：随着S₁/S₂的比值逐渐减小，集热器内部的高温区域愈发显著，平均温度愈高；这说明，当采光口尺寸不变时，增加集热器内壁面面积，可将集热器内部高温滞留区域占比变大，从另一方面说明，内壁面积的增加使得通过采光口溢出的热损逐渐变小。比较S₁/S₂为1/4和1/6的两种集热器云图可以发现，集热器顶部的高温滞留区占比随着S₁/S₂比值的减小而增大，且观察腔体底部温度为环境温度的流体区域占比可以发现，其低温区域占比随S₁/S₂比值的减小而减小，因此可以发现当S₁/S₂比值为1/6时，其平均温度高于S₁/S₂比值为1/4的球形集热器。

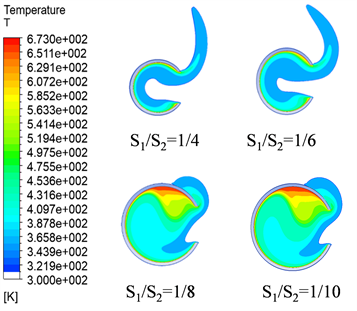
Figure 5. Temperature contour of collectors with different S₁/S₂ ratios

图5. 不同S₁/S₂比值下集热器的温度云图

此外，观察S₁/S₂比值为1/6的温度云图时，由于集热器顶部高温滞留区的增大，其流体外溢现象的速率减弱，即采光口处存在的较大温度梯度在一定程度上阻止了腔内流体外溢的趋势，使得热损进一步减弱。而当S₁/S₂比值为1/8和1/10时，其腔体底部温度与环境温度一致的流体区域占比显著减小，顶部高温滞留区的占比明显增大，说明此时外界流体进入腔体内部的趋势减弱，以及顶部流体外溢的趋势也减弱，即腔体内壁流体与出口流体自然对流现象减弱。其中高温滞留区域以及冷热流体的流场方向如图6所示。

Figure 6. Schematic diagram of flow field of spherical collector

图6. 球形集热器流场示意图

4.3. 采光口尺寸的设计优化

控制采光口面积与集热器内壁面最优比值为S₁/S₂ = 1/8、保持采光口倾角为0˚，通过改变开口尺寸(R₁ = 40、60、80、100、120 mm)，分析采光口尺寸大小对集热器热性能的影响，温度云图如图7所示。

Figure 7. Temperature contour of collectors with different aperture sizes(0˚ inclination)

图7. 不同开口尺寸下的温度云图(0˚倾角)

通过温度云图发现：当采光口尺寸逐渐增大时，集热器内部的低温对流换热区域逐渐增大，这说明，当开口尺寸较大时，集热器外侧流体受浮力因素影响而进入集热器内部的趋势较为明显，这导致对流换热现象剧烈。随着开口尺寸的逐渐增加，使得采光口顶部外逸的热空气流速逐渐增大，顶部热空气温度梯度逐渐增大，热量耗散上升。

观察图9发现，采光口中间位置流速近似为零，往两侧均呈逐渐增加的趋势，结合图8可以得出结论：采光口底部为冷流体自外侧环境进入集热器内部，而采光口顶部为热流体自腔体内部流向外侧环境，两股冷热流体在采光口中部相遇，速度方向相反造成速度减弱。并且，随着开口尺寸的逐渐增加，使得采光口顶部外逸的热空气流速逐渐增大，顶部热空气温度梯度逐渐增大，热量耗散上升。

Figure 8. The fluid temperature of daylighting port changes with the position (0˚ inclination)

图8. 采光口流体温度随位置变化(0˚倾角)

Figure 9. The fluid velocity of daylighting port changes with the position (0˚ inclination)

图9. 采光口流体速度随位置变化(0˚倾角)

此外，采光口的尺寸问题还和反射热损有关，其中有关公式如下：

${\alpha }_{cov}=\frac{{\alpha }_w}{1-\left(1-{\alpha }_w\right)\left(1-\frac{A_{ape}}{A_{re}}\right)}$ (10)

${\rho }_{cov}=1-{\alpha }_{cov}$ (11)

$P_{REFcov}={\rho }_{cov}{P}_{AP}$ (12)

式中： ${\alpha }_{cov}$ ——集热器有效吸收率；

${\alpha }_w$ ——腔体壁面材料对太阳辐射的吸收系数；

${\rho }_{cov}$ ——集热器反射率；

$P_{AP}$ ——集热器采光口截获的聚焦能量。

当 ${\alpha }_w$ 为定值时，开口面积等于集热器内表面积时，反射热损失最大，故应减少开口面积，但这同时降低了采光口截获的聚焦能量。因此，根据热学性能的热损而言，采光口的尺寸越大，热损失越大，但在实际操作中，一味降低采光口尺寸，在一定程度上使得入射光线进入腔体内部的总量降低，因此，需结合实际需求，在入射光线满足设计要求的范围内，尽可能地将开口尺寸设计的较小一些。

4.4. 采光口倾角的设计优化

固定量设定为S₁/S₂ = 1/8、R₁ = 60 mm，通过改变倾角(0˚、30˚、60˚、90˚)来研究集热器的静态热性能，定义倾角为集热器采光口平面的法线与水平面之间的夹角(如图10所示)：采光口面朝水平面时为0˚，开口面朝下为90˚。

由图10的温度云图可以看出：随着采光口的角度逐渐增大，集热器内部的高温滞留区域越发明显，这说明，采光口角度的增大使得高温滞留区逐渐变大，集热器与外界的换热逐渐减小。当倾角为0˚时，腔式集热器的内壁面温度线较为密度，温度梯度较大，与外界的对流换热现象较为剧烈。当倾角为30˚时，相较于0˚倾角而言，自集热器采光口外溢的流体温度明显降低，说明集热器与外界环境的对流换热减弱。当倾角为60˚时，集热器内部的上半部分主要是高温滞留区域，说明该处对流换热作用很弱，即外侧冷流体进入腔体内部的趋势减弱，热损进一步降低。

根据公式(3)~(8)计算得出不同倾角下集热器的热损失曲线如图11所示，随着采光口倾角逐渐增加，对流热损失逐渐变弱，说明倾角的增加可降低腔体内部温度由采光口溢出的可能，从而减弱了自然对流现象的产生，这与Leibfried [18] 观察到的试验现象一致。当倾角为最大值(90˚)时，其对流热损失值不为零，说明倾角的改变仅仅能降低对流热损失，而不能直接规避对流热损，因为，倾角的改变仅将腔体内部的温度分布趋于平均从而减弱采光口处的对流现象。此外，辐射热损失基本维持不变，说明倾角的变化对辐射热损的影响可忽略不计。因此，在实际工程中，应尽可能在高倾角下工作以降低对流热损，若倾角为最大值时，其对流热损占比仍较大时，可以考虑在采光口处增设高透光玻璃。

Figure 10. Temperature contour of collector at different inclinations

图10. 不同倾角下集热器的温度云图

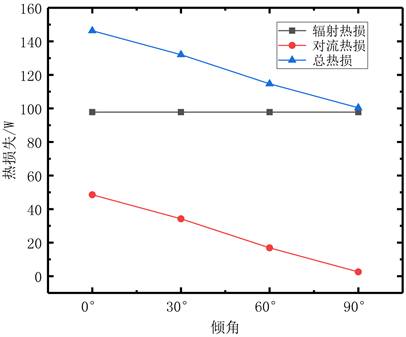
Figure 11. Comparison of heat loss of collectors at different inclinations

图11. 不同倾角下集热器的热损失比较

5. 结论

1) 对不同形状的集热器进行分析比对，得出球形集热器内的平均温度最高，温度外溢现象最弱，表征球形集热器的热损最小。

2) 随着S₁/S₂的比值逐渐减小，集热器的反射光损率逐渐减小，结合反射光损的下降速率可以看出，当S₁/S₂比值为1/8时光学效率较优；依据集热器内部的热性能分析可以发现集热器内部的高温滞留区域占比随着S₁/S₂比值的逐渐减小而增加，由此可见，当仅改变集热器内壁面积时，其集热器内部的温度梯度变化较大。结合上述影响分析，选定S₁/S₂比值为1/8时，其腔体的“保温效果”最优。

3) 当采光口尺寸逐渐增大时，其集热器内部的低温对流换热区域逐渐增加，这说明，当开口尺寸变大时，集热器外侧流体受浮力因素影响而进入集热器内部的趋势较为明显，这导致对流换热现象剧烈，热损增加。根据开口尺寸和热损的线性关系可知，应选择较小开口尺寸，但一味减少开口尺寸也在一定程度上限制了入射光线的总量，增加了高精度聚焦的技术压力，因此本文球形集热器的采光口尺寸选取为60 mm。

4) 当倾角为0˚时的对流热损失最大，倾角为90˚的对流热损失最小；当倾角改变时，仅仅带来自然对流的影响，而辐射热损并不受倾角的改变而产生变化。

NOTES

^*通讯作者。