1. 引言
磁流体力学(Magnetohydrodynamics,简称MHD)是研究等离子体和磁场相互作用的物理学分支。MHD-Boussinesq系统模拟由热场或密度场的浮力效应和磁场产生的洛伦兹力驱动的不可压缩流体的对流,这种对流发生在存在磁场的导电流体的水平层,它与Rayleigh-Benard对流的自然类型密切相关。本文研究如下形式的MHD-Boussinesq方程组的初值问题:
(1)
其中,
分别表示速度,磁场和温度,
表示压力,
是单位矢量
。
2009年,Hmidi T.和Keraani S. [1] 证明了当
时,Boussinesq方程组的初值问题存在整体解
。2017年,Larios A.和Pei Y. [2] 证明了当
时,初值问题(1)在
空间中存在局部解。2018年,Zhai X.和Chen Z. [3] 证明了当
且运动粘度依赖温度时,初值问题(1)
在
空间中存在整体解。2019年,Li Z., Liu P.和Niu P. [4] 证明了当
时,三维MHD方程组在
空间中存在整体解。
本文研究初值问题(1)在
空间中整体解的存在性,主要结果如下:
定理1.1设
且
,则初值问题(1)存在唯一的强解
,满足
本文中用到的符号:
·
表示C是仅依赖于
的常数。
· 如
表示C是仅依赖于
的常数。
·
表示具有傅里叶符号
的伪微分算子,其中
为Laplace算子。
· P表示Leray投影算子,被定义为 [4]
。
·
表示
空间中的内积。
· 设X和Y是Banach空间,
。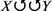 表示X紧嵌入到Y。
表示X紧嵌入到Y。
2. 初值问题(1)局部解的存在唯一性
为了研究初值问题(1)局部解的存在性,我们需要引用以下引理。
引理2.1 [5] (Aubin-Lions紧性引理)假定
是Banach空间且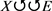 ,则
,则
1) 当
时, 。
。
2) 当
时,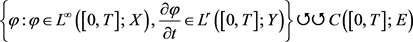 。
。
引理2.2 [6] 设
且
,则
为了证明初值问题(1)存在局部解,先引入初值问题(1)的磨光近似方程组的初值问题,任给
,
考虑
(2)
其中,
表示磨光算子。
将初值问题(2)视为
空间中的抽象常微分方程组的初值问题
(3)
由经典的Picard定理知,存在
,使得初值问题(3)有唯一的光滑解
引理2.3假设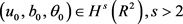 且
,则存在常数
,使得初值问题(1)存在唯一的局部强解
,满足
且
,则存在常数
,使得初值问题(1)存在唯一的局部强解
,满足
证明:在(2)的三个方程两边作用
,并分别与
作内积,再将左右两边分别相加,得
(4)
由Green公式,得
(5)
(6)
由Hölder不等式和引理2.2,得
(7)
类似地,有
(8)
(9)
(10)
由Green公式,得
(11)
类似地,有
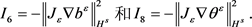 (12)
(12)
由Sobolev不等式,得
(13)
结合(4)~(13),得
(14)
由(14)和
及
知,存在一个不依赖于
的
,使得
(15)
由(15)和引理2.1知,存在
,满足
。当
时,解族
的子列
收敛,其极限
为初值问题(1)的解,且
下证初值问题(1)的局部解的唯一性。
设
和
是初值问题(1)的两个解。令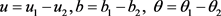 和
,则
满足
和
,则
满足
(16)
在初值问题(16)的三个方程两边分别与
和
作内积,再将左右两边分别相加,得到
(17)
由Green公式和
,得
(18)
由Hölder不等式和Sobolev嵌入定理,得
(19)
(20)
(21)
(22)
(23)
(24)
(25)
(26)
(27)
由Green公式,得
(28)
类似地,有
(29)
结合(17)~(29)知,存在
,使得
因此,对任意
,有
由Gronwall不等式及
,可得在
上恒有
,
即
。因此初值问题(1)的局部解唯一。引理2.3证毕。
3. 定理1.1的证明
为了研究初值问题(1)整体解的存在性,需用到如下引理。
引理3.1 [7] (Sobolev对数不等式)设
,则以下不等式成立:
为了证明初值问题(1)存在整体解,设
是初值问题(1)的解存在的最大时间区间,只需证明
。用反证法,假设
。在初值问题(1)中的方程两边分别与
作内积,用类似于引理2.3的证明方法,得
(30)
在初值问题(1)中的方程两边分别与
和
作内积,再将左右两边分别相加,得
(31)
由Gagliardo-Nirenberg不等式及Young不等式,得
(32)
类似地,有
(33)
(34)
(35)
结合(31)~(35)知,存在
,使得
由Gronwall不等式及(30)得,
在
中有界。
在方程组(1)的两边作用
并分别与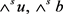 和
作内积,再将左右两边分别相加,得到
和
作内积,再将左右两边分别相加,得到
(36)
类似
和
的估计方法,可得关于
和
的如下估计,
(37)
(38)
(39)
(40)
由Sobolev不等式,得
(41)
由Green公式,得
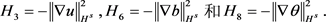 (42)
(42)
结合(36)~(42)知,存在
,使得,
由Gronwall不等式,得
由引理3.1可证,对任意
,有
因此,
从而,
由Gronwall不等式得
。又由
知,解可被延拓到
后,这与
为初值问题(1)的解的最大存在区间的假设相矛盾,因此
。定理1.1证毕。