1. 引言
21世纪以来能源危机和环境污染的问题越加严重,汽车产量的巨大需求加快了能源的消耗,如何降低汽车能耗成为了关注的对象,而汽车轻量化是解决这一问题的较好措施。铝合金型材因其密度低、强度高、耐腐蚀等优点,成为了汽车轻量化技术中合适的材料选择,在汽车制造、加工等方面应用广泛 [1]。
近几年,交通用铝占比达到了25%左右,属于第二大用铝行业,铝合金在市场的需求量逐步增加。相比于钢材,铝合金伸缩率小、弹性系数低,主要用于制造汽车结构件。在汽车零部件的加工过程中,弯曲成型是影响产品质量的一个重要步骤,在素材弯曲成型时,回弹是必须考虑的因素。回弹过大或过小都会导致弯曲件尺寸精度低或产生缺陷等,并且增加模具设计的难度,加大后续试模、修模的工作量 [2] [3] [4] [5]。素材的不规则截面和变截面,也使得弯曲回弹问题成为汽车零部件厂商关注的热点 [6] [7]。本文针对该问题进行分析研究,采用数值模拟对铝合金型材进行三维建模,模拟素材的弯曲回弹过程,得到成型回弹的数据结果,研究不同的成型原因和回弹的影响因素。通过对产品的测量与对比,预测弯曲回弹量,控制回弹大小,在模具的设计过程中,对回弹量进行一定的补偿,进而生产出尺寸合格、精度较高的零部件,为实际的加工生产提供可靠的依据和支持 [8] [9]。
2. 实验材料与方法
2.1. 材料力学性能测试
本工作中铝合金型材弯曲成型采用的素材是6063铝合金,其化学成分如表1所示。

Table 1. Chemical composition of 6063 aluminum alloy (%, mass fraction)
表1. 6063铝合金的化学成分(%,质量分数)
在电子万能材料试验机上进行素材的室温拉伸试验,从铝挤出并时效好的素材中切割一部分作为拉伸试样,其长度为300 mm。通过对时效温度为140℃的产品素材进行拉伸试验获得工程应力–应变曲线,如图1所示。
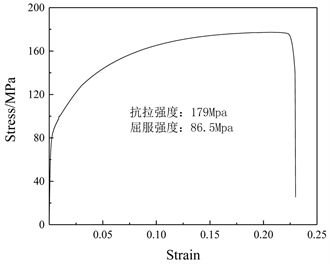
Figure 1. Stress-strain curve when the aging temperature is 140˚C
图1. 时效温度为140℃时产品应力–应变曲线
由图1可见,素材在拉伸实验中经历了弹性变形阶段、屈服阶段、塑性强化阶段、缩颈变形阶段。弹性阶段中变形为可逆的,卸载后变形完全恢复;屈服阶段结束后,试样在塑性变形下产生应变,应力不断上升;试样在缩颈变形阶段时力不再增加,开始出现小裂纹,产生缩颈变形,最后完全断裂。
2.2. 成型工艺及试件实验
应用弯曲机和CNC机器人进行弯铣一体化技术,通过材料和结构的轻量化有效减轻了汽车质量,成为汽车节能减排的重要措施 [10]。铝合金素材采用双臂伺服弯曲机进行CNC拉弯,先将素材进行预拉,然后拉弯成型至贴模,稳定后卸载回弹,获得实际产品。结果如图2所示,时效温度为140℃的素材在回弹后与产品尺寸比较吻合,成型工艺对回弹量的影响较小。素材最大的回弹主要集中在端部,主要原因是弯曲角度在端部最大,约束载荷也造成截面处的拉应力和压应力分布较大。在成型过程中,素材由弹性变形阶段进入塑性变形,而固定端最先进入塑性变形阶段,当卸载弹性回复后,在固定端的塑性变形量较大。弯曲时素材A面受到的拉应力大于B面受到的拉应力,因此A面的变形更为明显。弯曲件外表面无明显裂纹或“橘皮现象”表明试件产品合格,实验结果较优。
3. 铝合金型材弯曲回弹模拟
3.1. 建立模型与模拟参数设置
本文采用ABAQUS非线性有限元分析软件对铝合金型材弯曲回弹过程进行模拟分析。模拟采用了6063系铝合金型材,长1200 mm、宽18 mm、厚1 mm。材料密度2.7 × 103 kg/m3,杨氏模量为5.7 × 104,泊松比0.33,弹塑性参数选取本文实验数据,模型整体结构如图3所示。
产品弯曲成型为大变形,素材在弯曲和回弹过程中几何、材料和接触都是非线性的,同时型材弯曲回弹是一个多重非线性耦合的复杂过程,在回弹模拟中,根据精度要求,需要相对小的回弹误差和准确的回弹变形量 [11]。因此本文针对模型进行了局部网格的细化,并分为两个分析步进行模拟,从而节省计算时间和提高收敛性。素材与模具之间的成型面为面接触,将两者间的摩擦系数设置为0.1。为保证计算精度,网格采用自适应动态划分 [12] [13]。
3.2. 模拟与实验的结果对比
从本工作中的模拟结果表明成型贴模情况良好,回弹计算精度较高,无明显的失真波动现象。Y向实际回弹距离27.6 mm,Y向模拟回弹距离36.1 mm,吻合度达76.45%,相对误差23.5%;Z向实际回弹27.18 mm,Z向模拟回弹24.09 mm,吻合度达88.63%,相对误差11.3%。模拟回弹与实验结果在线弧、面弧均有偏差量,面弧偏差更小。通过实验与模拟的对比,弯曲和回弹的趋势基本一致,较好地体现了模拟计算的适用性和准确性。
3.3. 弯曲回弹前后的应力–应变分析
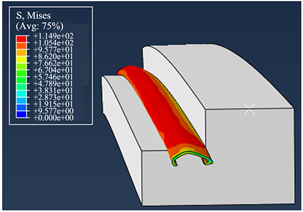
成型模拟中,素材右端面采用端部速度控制,以右部端面为Y-Z坐标平面,使端面沿Y和Z方向在一定时间内进行指定速度的移动,移动终止位置为完全贴模时。素材贴模后进行卸载回弹,获得回弹模拟结果。素材的成型与回弹终止时应力结果如图4、图5所示。
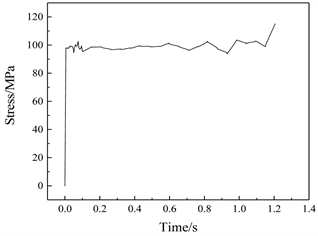
从图4(a)、图4(b)可以看出回弹前后素材的应力分布呈现出从左到右变大的趋势,应力最大处在素材右端(固定端为左),由于卸载使得回弹后的整体应力值均小于回弹前的应力值。图5(a)、图5(b)显示了成型过程中应力最大处的变化趋势,素材在加载过程中,应力随着时间增加而增加,在加载结束时,素材完全贴模;在卸载过程中,应力逐渐减小,模拟的结果符合实验结果,为实际生产提供了较好的理论基础。
 (a)
(a)  (b)
(b)
Figure 4. (a) Equivalent stress distribution before springback; (b) Equivalent stress distribution after rebound
图4. (a) 回弹前等效应力分布;(b) 回弹后等效应力分布
 (a)
(a)  (b)
(b)
Figure 5. (a) Stress-time diagram before rebound; (b) Stress-time diagram after rebound
图5. (a) 回弹前应力–时间图;(b) 回弹后应力–时间图
为了进一步分析素材的回弹情况,其等效塑性应变和应变分布见图6、图7所示。图6(a)、图6(b)结果表明回弹前后素材的等效塑性应变分布从左到右逐渐减小,最大处在素材固定端,表明在成型过程中固定端受约束影响塑性应变较大。图7(a)、图7(b)显示了回弹前后的应变分布,由于素材的部分弹性回复,应力释放,回弹后各部分对应的应变值明显小于回弹前的应变值,应变最大处在素材右端,应力应变最大处基本在同一位置,模拟的应力应变结果符合实验结果,验证了模拟计算的可靠性和准确性。
 (a)
(a)  (b)
(b)
Figure 6. (a) Equivalent plastic strain before springback; (b) Equivalent plastic strain after springback
图6. (a) 回弹前等效塑性应变;(b) 回弹后等效塑性应变
 (a)
(a)  (b)
(b)
Figure 7. (a) Strain distribution before springback; (b) Strain distribution after springback
图7. (a) 回弹前应变分布;(b) 回弹后应变分布
4. 不同阻尼系数对弯曲回弹的影响
回弹主要表现为整体卸载回弹、切边回弹和局部卸载回弹,当回弹量超过允许误差后,就会出现成型缺陷,导致零件的尺寸精度不合格。在模拟过程中,弯曲回弹的素材作为可变形体,阻尼系数会对弯曲的回弹量产生影响 [14]。通过对不同阻尼系数的回弹模拟,可以获得与回弹量误差之间的对应关系和影响规律,结果如图8所示。
 (a)
(a) 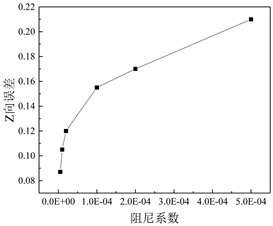 (b)
(b)
Figure 8. (a) Y-direction rebound error-damping coefficient curve; (b) Z-direction rebound error-damping coefficient curve
图8. (a) Y向回弹量误差–阻尼系数曲线;(b) Z向回弹量误差–阻尼系数曲线
从图8(a)、图8(b)中可以看出Y向的回弹偏差随着阻尼系数的增大而减小,误差最小在12%,阻尼系数为5e−4,但对于模拟的收敛性也相应变差;Z向的回弹偏差随着阻尼系数的增大而增大,误差最小在10%左右,阻尼系数为1e−5,同时表现出对弯曲回弹量有较大的敏感性。虽然不同阻尼系数的仿真结果与实际产品存在差异,但是在回弹方向上基本一致,并且整体部位的回弹与实验结果符合较好。
5. 结论
1) 针对铝合金弯曲回弹的数值模拟,建立了三维有限元模型,模拟了型材的弯曲回弹过程,分析了回弹的影响因素。通过模拟与实验的结果对比,验证了模拟的可靠性和准确性。
2) 模拟与实验结果的回弹趋势吻合较好,回弹前应力随时间增加而增加,回弹前各部分应力、应变值均大于回弹后的应力、应变值,应力应变最大处基本在同一位置。通过对应力、应变的变化分析出素材弯曲回弹的风险点,提前做好预处理,为模具设计提供科学依据,优化模具设计。
3) 通过改变回弹阻尼系数进行模拟分析,结果表明Y向的回弹偏差随阻尼系数增大而减小,误差最小在12%,阻尼系数为5e−4;Z向的回弹偏差随阻尼系数增大而增大,误差最小在10%,阻尼系数为1e−5。对阻尼系数的研究可以有效分析回弹量,提高产品尺寸精度。