GR4J与新安江模型在湿润地区比较研究

Comparative Study of GR4J and Xinanjiang Models in Humid Area

摘要: 为了比较不同水文模型在湿润地区的预报能力和效果，选用新安江流域上游屯溪水文站控制流域作为研究区域，分别利用GR4J和新安江模型对流域进行水文模拟，并开展洪水概率预报研究。结果表明：两个模型在湿润流域的模拟效果相当且都较好，GR4J和新安江模型模拟率定期和检验期的纳什效率系数(NSE)均达到90%以上，且相对误差(RE)较小；两模型在湿润流域均能进行可靠的概率预报，GR4J率定期和检验期的连续概率排位分数(CRPS)为18.73 m3/s、12.57 m3/s，其概率预报评价指标均相对于新安江模型更优，在概率预报方面性能稍好，精度较高；简单和复杂的模型在非特定条件下，可以取得同样效果，湿润地区的径流模拟、预报洪水可选择简单快捷的模型。

Abstract: In order to compare the forecasting abilities and effects of different hydrological models in humid areas, GR4J and Xinanjiang models were used to simulate runoff and probability flood forecasts in the Tunxi basin. The results were summarized as follows: Nash-Sutcliffe efficiency coefficient (NSE) are both over 90% in calibration and validation period, the Relative error (RE) values are also small. Both models can carry out reliable probabilistic forecasts in humid basins. The Continuous ranked probability score (CRPS) values of GR4J in calibration and validation period are 18.73 m3/s and 12.57 m3/s respectively; moreover, most of its probabilistic forecast evaluation indicators are better than Xinanjiang model. GR4J model performs with higher accuracy in probabilistic forecasting. Simple and complex models can achieve the same effect under non-specific conditions, GR4J model is preferred for runoff simulation and flood forecasting in humid areas.

1. 引言

水文预报是我国防汛、水资源开发利用的重要依据 [1]。由于自然界水文现象在多种因素共同影响的作用下十分复杂，其真正的机理仍然没有被大家完全掌握，水文模型成为了分析研究水文现象的重要工具之一。流域水文模型是为了解决水文预报、水资源管理规划、水文分析计算等问题所开发的工具；是将流域当作一个系统，模拟流域的各种过程(物理、化学、生物)所建立的数学或实体结构。随着各种技术的飞速发展，水文模型也日渐复杂，更多的水文模型结合了地形、气象等多种影响因素。但是越是复杂的水文模型越需要更多的参数，可能造成误差的叠加等问题。邓鹏 [2] 等人在研究中发现结构越复杂、考虑越全面的某些分布式水文模型可能在洪水模拟上结果不如传统的概念性模型。徐宗学 [3] 也提出了流域处于湿润地区，简单模型和复杂模型可以取得同样效果的观点。

由于很多不确定性因素共同影响着水文过程，流域水文模型因而存在广泛的不确定性。影响水文过程的自然因素本身就具有很明显的无序性、不稳定性等性质。在排除自然因素影响下，模型不确定性大致归纳为三类：模型结构本身不确定性、模型输入不确定性和模型参数不确定性 [4]。不同原因导致的误差相互作用、叠加，从而最终造成模型模拟结果的不准确。综合不确定性分析是综合考虑了两到三类不确定性来源，贝叶斯预报处理器(Bayesian Processor of Forecast, BPF)是综合不确定性分析方法之一，它是对确定性预报后处理进行概率预报。Krzysztofowicz [5] 结合了基于预报值和实测值的先验分布和似然函数，输出实测值的条件后验分布函数，将不确定的预测转化为最优决策模型。Krzysztofowicz [6] 首先对先验分布以及似然函数进行线性–正态假设，提出线性–正态贝叶斯预报处理器(Linear-Normal BPF)，但是此假设忽略了大多数水文过程都是非线性、非正态的。Krzysztofowicz和Evans [7] 后续提出亚高斯贝叶斯预报处理器(meta-Guassian BPF)，但转换处理过程仍存在缺陷，影响其适用范围 [8]。考虑到大部分水文过程所服从分布的多样性，刘章君 [9] 等利用Copula函数的边缘分布可以为任意分布的特性，提出基于Copula函数的贝叶斯预报处理器(Copula-BPF)，将其应用在三峡水库入库洪水的概率预报中，发现其在预报径流总量方面效果好、适用范围广。

2. 模型和方法简介

2.1. GR4J

GR4J (modèle du Génie Rural à 4 paramètres Journalier)是降雨径流模型之一，Perrin [10] 开发并已证明其在建模方面有很强的基础性和有效性。该模型采用产流水库、汇流水库这两个线性水库进行产汇流计算，对湿润地区进行洪水预报和水资源规划方面具有简便、准确等特点。模型只包含4个参数，分别是：x₁产流水库容量(mm)，x₂地下水交换系数(mm)，x₃汇流水库容量(mm)，x₄单位线汇流时间(day)。本文选用GR4J作为简单模型进行水文模拟和预报研究。

2.2. 新安江模型

新安江模型于1973年开发，1980年赵人俊 [11] 团队发表。该模型分为四个层次：蒸散发采用三层蒸散发模型、产流为蓄满产流模式、水源划分有二水源及三水源、汇流有坡地和河道汇流。新安江模型主要特点是蓄满产流的概念，即在包气带的土壤含水量达到田间持水量后，才产生径流，此后径流量等于不再发生损失的降雨量。本文选用三水源新安江模型作为复杂模型进行水文模拟和预报研究，该模型共有15个参数，各参数都有明确的物理意义。

2.3. SCEM-UA全局优化算法

本文采用的GR4J、新安江模型均运用SCEM-UA (Shuffled Complex Evolution Metropolis global optimization algorithm)进行参数率定。Vrugt [12] 等人提出了将SCE-UA (Shuffled Complex Evolution)算法和MCMC (Markov Chain Monte Carlo)方法融合得到SCEM-UA算法。该算法是鲁棒性的全局优化方法，SCE-UA中所用到的下山单纯形法被HM (Metropolis Hastings strategy)法取代，新样本的推荐分布除了依据先验分布，也能在计算的同时得到更新。SCEM-UA算法采用马尔可夫链避免对采样集合的再划分，用蒙特卡洛采样方法从链中选取样本，在不断向目标后验概率演化的过程中使得计算量减小，效率提高。由于GR4J模型4个参数均为敏感性参数，且新安江模型参数较多、敏感性参数占比很大，选用SCEM-UA算法可以高效且准确率定出模型参数组。

2.4. 基于Copula函数的贝叶斯预报处理器

设h、s分别为随机变量实测流量和确定性预报流量H、S的实现值，由贝叶斯理论可以得到实际流量H的后验函数密度为

${\varphi }_k\left(h_k|s_k\right)=\frac{f_k\left(s_k|h_k\right)\cdot g_k\left(h_k\right)}{{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{f}_k\left(s_k|h_k\right)\cdot g_k\left(h_k\right)d{h}_k}}$ (1)

式中：k为预见期长度。S_k = s_k的前提下， $f_k\left(s_k|h_k\right)$ 为H_k的似然函数，g_k(h_k)为实测流量H_k的先验密度。

Copula-BPF中，实测流量序列和预报流量序列构造其边缘分布，Sklar定理构造二维联合分布，实测序列的后验分布即为联合分布的条件分布函数 [13]。

Sklar定理描述的是，对任意的 $x\in R^n$，总存在一个n-Copula函数C使得

$H\left(x_1,x_2,\cdots ,x_n\right)=C_{\theta }\left(F_1\left(x_1\right),F_2\left(x_2\right),\cdots ,F_n\left(x_n\right)\right)$ (2)

式中：θ为Copula函数的参数。 $H\left(x_1,x_2,\cdots ,x_n\right)$ 为n维向量的联合分布函数， $F_1\left(x_1\right),F_2\left(x_2\right),\cdots ,F_n\left(x_n\right)$ 为向量的边缘分布。

在Sklar定理中n取2时，即可构造实测流量序列和预报流量序列H、S的二维Copula函数。H、S的边缘分布为 $u=G\left(h\right)$ 、 $v=F\left(s\right)$，相应密度函数表示为 $g\left(h\right)$ 、 $f\left(s\right)$。u，v的联合分布可表示为

$F\left(h,s\right)=C_{\theta }\left(G\left(h\right),F\left(s\right)\right)=C_{\theta }\left(u,v\right)$ (3)

给定预报值的前提下，实测序列H的条件后验分布函数和条件后验密度函数为

$\Phi \left(h|s\right)=P\left(H\le h|S=s\right)=P\left(U\le u|V=v\right)=\frac{\partial C_{\theta }\left(u,v\right)}{\partial v}$ (4)

$\varphi \left(h|s\right)=\frac{\text{d}\Phi \left(h|s\right)}{\text{d}h}=\frac{{\partial }^2{C}_{\theta }\left(u,v\right)}{\partial u\partial v}\cdot \frac{\text{d}u}{\text{d}h}=c_{\theta }\left(u,v\right)\cdot g\left(h\right)$ (5)

式中： $\text{Φ}\left(h|s\right)$ 、 $\varphi \left(h|s\right)$ 为实测序列H的条件后验分布函数和条件后验密度函数， $c_{\theta }\left(u,v\right)$ 为联合密度函数。

3. 评价指标

3.1. 确定性预报评价指标

用以评价水文模拟效果的评价指标有水量相对误差RE、纳什效率系数NSE、相关性系数R [14]。水量相对误差RE越小，说明模拟值越接近实测值，模拟值的可信度越高。纳什效率系数NSE用来验证水文模型模拟结果，NSE越接近1，表示模型可信度高且质量好。模型的确定性预报序列和实测值序列具有相关性，相关性用相关性系数R表示，R越大，表示两序列的相关性越高。

3.2. 概率预报评价指标

3.2.1. 置信区间评价指标

平均带宽B、平均相对带宽RB、覆盖率CR都反映了概率预报置信区间的效果。平均带宽B、平均相对带宽RB越小，说明相同置信度下的置信区间越窄，概率预报的不确定性越小。覆盖率CR越大，说明观测值被置信区间捕捉到的概率越大，而CR值越接近选定的置信水平(本文为90%)说明概率预报区间效果越好 [15]。

$B=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}\left(\overline{h_i}-\underset{\_}{h_i}\right)}$ (6)

$RB=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}\left(\frac{\overline{h_i}-\underset{\_}{h_i}}{h_i}\right)}\times 100\%$ (7)

$CR=\frac{N_c}{N}\times 100\%$ (8)

式中： $\overline{h_i}$ 表示为预报i时刻区间上界， $\underset{\_}{h_i}$ 为预报i时刻区间下界， $h_i$ 为i时刻实测值。 $N_c$ 为被置信区间所覆盖的实测点数，N为全部实测点数。

3.2.2. 概率预报综合评价指标

可靠性(α-index)用于比较预报与实测概率分布的差异。P值为某时刻实测流量值对应的概率预报的分布函数值，如果预报准确，P值应该符合均匀分布U(0,1)。P值所服从的分布函数与均匀分布的差距越小说明预报越准确 [16]。α-index越接近1，说明预报越可靠。

$\alpha -index=1-\frac{2}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}\left(\left|q_i^t-q_i^e\right|\right)}$ (9)

式中： $q_i^t$ 为标准均匀分布的分位数， $q_i^e$ 为P值分位数。

连续概率排位分数(CRPS)越小说明概率预报越准确可靠 [17]，确定性预报时CRPS的公式变为平均绝对误差(MAE)。

$CRPS=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\left[F_i\left(r\right)-H_s\left(r-h_i\right)\right]}^2\text{d}r}}$ (10)

式中： $F_i\left(r\right)$ 是i时刻流量r对应的预报累积分布函数值。 $H_s\left(r-h_i\right)$ 是实际流量的累积分布函数，其取值为：

$H_s\left(r-h_i\right)=\{\begin{array}{l}0r<h_i\\ 1r\ge h_i\end{array}$ (11)

4. 研究区域

屯溪水文站于1950年6月设立，是国家重要水文站，其地理位置在118’20'E，29’43’N。作为新安江干流上游主要的控制站之一，其控制流域面积为2679 km²，主要支流有率水、横江。屯溪流域处于北亚热带，是安徽省的多雨中心区，年降雨量1280~1700 mm，其中春雨占年降雨量30%左右，汛期雨占50%左右。5~6月雨量占全年最多，且多为暴雨。夏季易受梅雨影响，雨量大。有旱涝、暴雨等灾害天气。屯溪流域年平均气温15.4℃~16.4℃，全年低温多数处于零上。屯溪流域是典型湿润地区，干燥度 < 1.00，空气湿润，蒸发量小。

流量资料由水文年鉴获得1997~2005年屯溪水文站逐日实测流量数据资料；流域河网水系资料由地理空间数据云网站下载获得区域数字高程数据SRTM-DEM数据。通过收集获得1997~2005年屯溪流域内11个雨量站的逐日降水数据资料、屯溪流域内蒸发站蒸发皿1997~2005年逐日蒸发资料。

5. 结果分析

5.1. 水文模拟结果对比

利用SCEM-UA算法，综合考虑GR4J以及新安江模型的参数数目、特性、取值范围等，分别设置SCEM-UA算法，人工调试的同时利用SCEM-UA算法找到最优参数组应用在两模型中。选取1997年为预热期，1998年至2002年共5年为率定期，2003年至2005年共3年为检验期。

通过GR4J以及新安江模型进行的水文模拟，计算不同模型不同时期的评价指标如表1所示。结果显示，两模型模拟流量与实测流量的纳什效率系数(NSE)均达到了0.9以上。这表明两模型在屯溪水文站控制流域应用效果整体都较好。从总径流量的相对误差(RE)指标看：新安江模型的RE均比GR4J的RE小。率定期RE均在5%以内，说明率定期模拟效果很好。检验期RE超过5%，均在9%范围内，说明检验期两模型模拟效果均较差；检验期RE显示为正值，说明模拟值高估了真实值。

分析原因：(a) 主要原因：率定期包含了特殊年份1998年和1999年大洪水，而检验期3年没有水情较大的年份。1998年安徽省全省受98年全国气候和大洪水影响，新安江流域也有较大降雨；1999年新安江流域发生了“99·7”特大暴雨洪水 [18]。两年特殊年份的降雨径流资料导致模拟值出现低估实际径流的现象。同时，率定期极端洪水事件导致率定的参数组不适用于普通情况，这导致检验期的模拟值高估了真实值。(b) 改进方案：率定期选取大洪水系列是偏安全的，有利于预报暴雨洪水，大水信息包含在参数中，自然对检验期的小水照顾不够。

根据贝叶斯概率预报的概念，概率预报效果的好坏与实测径流量H、模型的模拟值S的相关性有关，表1中计算所得不同模型不同时段的相关性系数(R)表明：GR4J和新安江模型的模型输出值与实测值相关性都很好，GR4J的相关性略优于新安江模型。

综上，GR4J和新安江模型模拟能力相当。GR4J模拟值的NSE更接近理想值，新安江模拟值的相对误差更小。

Table 1. Simulation results for two hydrological models

表1. 不同模型径流模拟评价指标

5.2. 概率预报结果对比

5.2.1. 分布拟合

本文选择使用Copula-BPF预报处理器对GR4J和新安江模型的模拟值进行后处理。从水文领域较普遍使用的线型中选择Gamma分布、正态分布(NOR)、对数正态分布(Log-NOR)、Gumbel分布共四种线性 [19] 对实测和模拟径流边缘分布进行拟合；选用Copula函数族中的二维Archimedean Copula函数用以构造实测值与模拟值的联合分布，常用的二维Archimedean Copula函数有Gumbel-Hougaard、Clayton、Frank三种 [20]。选用均方根误差(Root Mean Square Error, RMSE)筛选最佳理论分布线型。RMSE越小说明理论分布与经验分布拟合情况较好 [21]。在进行多次组合实验并结合拟合的RMSE值后，本文最终选定Gamma分布和Gumbel-Hougaard函数来构造Copula-BPF预报处理器的边缘分布和联合分布。

由贝叶斯理论的概念，当给定任意时刻的模拟值S_x或S_g，则可以得到其实测值的后验分布。如下图1和图2所示，选取2001年6月10日为例，不同模型输出进行Copula-BPF处理后的先验密度与先验分布、后验密度与后验分布的对比图。2001年6月10日的实测流量为200 m³/s，后验密度表现出偏正态的特性，且最大概率处对应流量值更逼近真实值。综合所有时刻的后验分布情况，可知经过贝叶斯修正后的后验分布更能准确描述实测值的分布情况，且GR4J经过Copula-BPF处理的后验密度分布比新安江模型经过Copula-BPF处理的后验密度分布更加集中，概率密度峰值更明显。

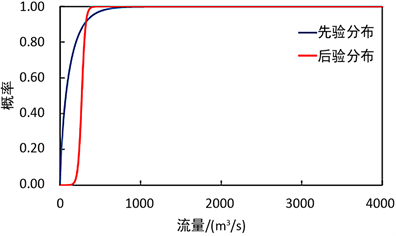(a) 先验及后验分布函数 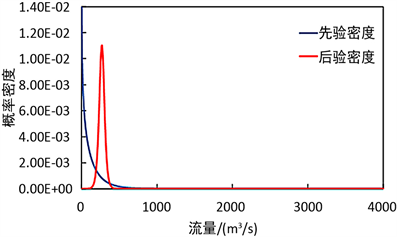(b) 先验及后验密度函数

Figure 1. Prior and posterior density of observation H on 10 June 2001 by using GR4J

图1. 2001年6月10日GR4J流量先验和后验密度及分布函数

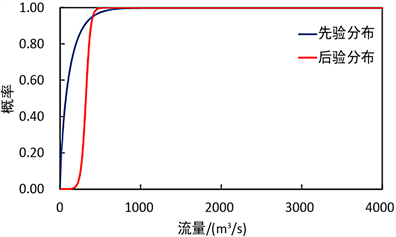(a) 先验及后验分布函数 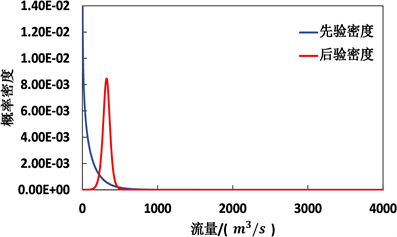(b) 先验及后验密度函数

Figure 2. Prior and posterior density of observation H on 10 June 2001 by using Xinanjiang model

图2. 2001年6月10日新安江模型流量先验和后验密度及分布函数

5.2.2. 基于后验概率的预报评价

选择Copula-BPF概率预报的条件最可能值h_m作为修正后确定性预报的径流量。对比模型预报与概率预报修正数值的评价指标，结果在表2中展示。

从表2可以看出，模型模拟输出值作为确定性预报已经足够准确。概率预报修正后的径流量在NSE上与确定性预报结果基本一致，在率定期的RE上修正效果不佳，在检验期RE值略有改进。结合以上信息，Copula-BPF法对GR4J和新安江模型的确定性预报的修正作用不显著。

Table 2. Comparison of deterministic forecast results and BPF corrected value

表2. 模型模拟输出值与BPF修正值结果比较

5.2.3. 置信区间对比

取预报区间的置信水平为90%，90%置信区间在包含实测点的前提下越窄，表明预报的不确定性越小。由于流量序列长度限制，选取率定期2001年4至8月和检验期2004年4至8月绘制局部图，图3、图4中展示了实测值后验分布的90%置信区间以及实测值点据。分析整个率定期、检验期可知，绝大部分实测流量都较好地被90%置信区间所包含，其中GR4J的预报不确定性更小。高流量区尤其是洪峰处存在明显跃出置信区间的现象，说明GR4J以及新安江模型的概率预报对高流量区的捕捉不够准确。

计算不同模型的概率预报评价指标得到表3。根据在相同的置信度之下，置信区间越小则模型的不确定性越低的规律，可以得到GR4J概率预报的平均带宽(B)，相对带宽(RB)在率定与检验期都比新安江模型概率预报低；同时根据预报区间所覆盖的实测值越多，说明预报更准确的规律，GR4J的覆盖率(CR)在率定期和检验期都比新安江模型概率预报所对应的值高。

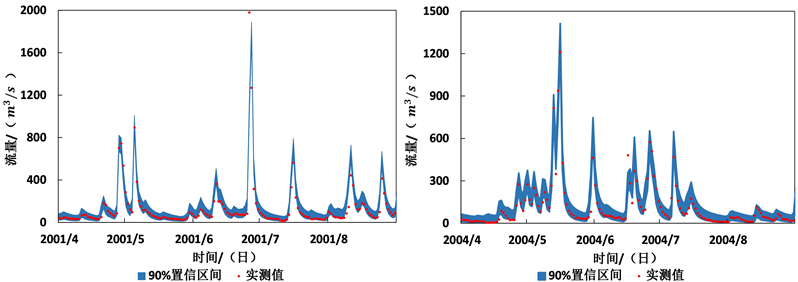
Figure 3. The observed runoff processes and its 90% confidence interval by using GR4J

图3. GR4J 90%置信区间与观测值拟合情况局部图

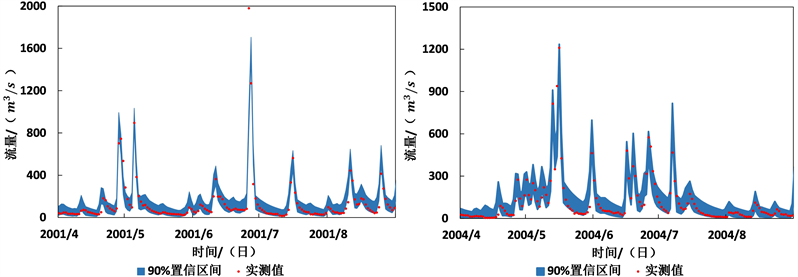
Figure 4. The observed runoff processes and its 90% confidence interval by using Xinanjiang model

图4. 新安江模型90%置信区间与观测值拟合情况

Table 3. Results for assessment of the Copula-BPF prediction bounds

表3. 不同模型概率预报置信区间评价指标

5.2.4. 概率预报结果对比

对GR4J和新安江模型的概率预报性能进行整体评价，得到如表4所示参数。GR4J和新安江模型率定期存在低估预报不确定性的现象，率定期和检验期都存在整体预报偏低的现象，率定期的α-index明显大于检验期的α-index。低估预报不确定性可能与未考虑到的其它不确定性来源有关，整体预报偏低的现象与5.2.3节所讨论的高流量区超出置信区间的现象相吻合。根据CPRS的定义，概率预报相比于确定性预报在CRPS上都有明显的降低，体现了概率预报的优势。同时，GR4J在不同时期的CRPS值都比新安江模型的CRPS值低，这说明GR4J在概率预报方面相比于新安江模型更加的合理可信。

Table 4. Comprehensive evaluation index for probability forecast of different models

表4. 不同模型概率预报综合评价指标

6. 结论与展望

本文选取屯溪水文站控制的流域作为研究对象，其满足湿润、简单地区的要求，且降雨、蒸发、径流等资料较为丰富。使用GR4J、新安江模型分别模拟降雨径流过程，得到模拟径流值。使用基于Copula函数的贝叶斯预报处理器(Copula-BPF)对模拟值进行后处理，得到概率预报结果。结论如下：

1) 对比两模型模拟径流值的评价指标及模拟流量过程线：可以发现GR4J和新安江模型在模拟屯溪流域的降雨径流过程能力上都较好，也都存在模拟流量不能准确模拟高流量区径流的现象。选用概率预报处理后的数值代替模型输出值进行确定性预报的效果不明显。

2) 比较两模型概率预报90%置信区间结果显示：GR4J和新安江模型的90%置信区间均能够较好覆盖实测流量值。在相同置信度下，GR4J的置信区间更窄、覆盖率更高，说明其不确定性相对更小。比较两模型概率预报综合评价指标，结果表明：GR4J和新安江模型的概率预报都有较高可靠性，且概率预报比确定性预报在CRPS上均存在超过10%的降幅，说明概率预报的效果要比确定性预报好很多。对比评价指标的数值，GR4J的概率预报综合效果整体好于新安江模型，可靠性(α-index)、连续概率排位分数(CRPS)都更趋近于理想值。

3) 在确定性预报中：新安江模型由于有15个需率定参数，且敏感性参数较多，最优参数组的确定耗时较长，虽然效果很好但工作量较大。GR4J只有4个参数，在率参中可以有效降低工作量。在概率预报中：根据贝叶斯概率预报的概念，GR4J结构简单，且确定性预报值与实测值的相关性更好，这使GR4J概率预报能力更佳。新安江模型的确定性预报值与实测值的相关性相对于GR4J较低，所以概率预报效果比G4RJ略差。

4) GR4J和新安江模型都可用来进行屯溪水文站控制流域的确定性水文预报、概率水文预报，且精度都较高。新安江模型和GR4J在湿润地区确定性预报效果相当，概率预报GR4J性能略优于新安江模型。因此，在湿润的大流域地区可选用较为简单的水文模型GR4J开展相关研究。

基金项目

国家自然科学基金地区联合基金项目(U20A20317)资助。

参考文献